
Question Number 61269 by alphaprime last updated on 31/May/19
![Let p(x) be a quadratic polynomial such that for distinct α and β , p(α) = α and p(β) =β prove that α and β are roots of p[p(x)]−x=0 Find the remaining roots .](Q61269.png)
$${Let}\:{p}\left({x}\right)\:{be}\:{a}\:{quadratic}\:{polynomial}\:{such} \\ $$$${that}\:{for}\:{distinct}\:\alpha\:{and}\:\beta\:, \\ $$$${p}\left(\alpha\right)\:=\:\alpha\:{and}\:{p}\left(\beta\right)\:=\beta \\ $$$${prove}\:{that}\:\alpha\:{and}\:\beta\:{are}\:{roots}\:{of}\:\:{p}\left[{p}\left({x}\right)\right]−{x}=\mathrm{0}\: \\ $$$${Find}\:{the}\:{remaining}\:{roots}\:. \\ $$
Answered by ajfour last updated on 31/May/19
![p(x)=a(x−h)^2 +k α, β are roots of a(r−h)^2 −r+k=0 ...(i) p[p(x)]−x=a{a(x−h)^2 +k−h}^2 +k−x And since from (i) a(r−h)^2 +k=r ....(ii) p[p(r)]−r=a{a(x−r)^2 +k−h}^2 −r+k using (ii) we get p[p(r)]−r=a{r−h}^2 −r+k =0 using (i) hence α,β are roots of p[p(x)]−x=0 . Again p[p(x)]−x=a{a(x−h)^2 +k−h}^2 +k−x or = a^3 (x−h)^4 +2a^2 (k−h)(x−h)^2 +a(k−h)^2 +k−x =a^3 x^4 −4a^3 hx^3 +[6a^3 h^2 +2a^2 (k−h)]x^2 −[4a^3 h^3 −+4a^2 h(k−h)+1]x +a^3 h^4 +2a^2 (k−h)h^2 +a(k−h)^2 +k Also lets assume p[p(x)]−x=a^3 [x^2 −(2ah+1)x+h^2 +(k/a)](x−γ)(x−δ) =a^3 {x^4 −(γ+δ+2ah+1)x^3 +[γδ+(2ah+1)(γ+δ)+h^2 +(k/a)]x^2 +(h^2 +(k/a))γδ} comparing the two expressions for p[p(x)]−x we conclude γ+δ = 4h−2ah−1 γδ(h^2 +(k/a))=a^3 h^4 +2a^2 (k−h)h^2 +a(k−h)^2 +k but from (i) 2h+(1/a)=α+β h^2 +(k/a)=αβ .....](Q61281.png)
$${p}\left({x}\right)={a}\left({x}−{h}\right)^{\mathrm{2}} +{k} \\ $$$$\alpha,\:\beta\:{are}\:{roots}\:{of} \\ $$$$\:\:{a}\left({r}−{h}\right)^{\mathrm{2}} −{r}+{k}=\mathrm{0}\:\:\:\:\:\:\:...\left({i}\right) \\ $$$${p}\left[{p}\left({x}\right)\right]−{x}={a}\left\{{a}\left({x}−{h}\right)^{\mathrm{2}} +{k}−{h}\right\}^{\mathrm{2}} +{k}−{x} \\ $$$${And}\:{since}\:{from}\:\left({i}\right) \\ $$$$\:\:\:\:\:{a}\left({r}−{h}\right)^{\mathrm{2}} +{k}={r}\:\:\:\:\:....\left({ii}\right) \\ $$$${p}\left[{p}\left({r}\right)\right]−{r}={a}\left\{{a}\left({x}−{r}\right)^{\mathrm{2}} +{k}−{h}\right\}^{\mathrm{2}} −{r}+{k} \\ $$$${using}\:\left({ii}\right)\:{we}\:{get} \\ $$$${p}\left[{p}\left({r}\right)\right]−{r}={a}\left\{{r}−{h}\right\}^{\mathrm{2}} −{r}+{k} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0}\:\:\:\:\:{using}\:\left({i}\right) \\ $$$${hence}\:\alpha,\beta\:{are}\:{roots}\:{of}\:{p}\left[{p}\left({x}\right)\right]−{x}=\mathrm{0}\:. \\ $$$${Again} \\ $$$${p}\left[{p}\left({x}\right)\right]−{x}={a}\left\{{a}\left({x}−{h}\right)^{\mathrm{2}} +{k}−{h}\right\}^{\mathrm{2}} +{k}−{x} \\ $$$${or}\:\:=\:{a}^{\mathrm{3}} \left({x}−{h}\right)^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{2}} \left({k}−{h}\right)\left({x}−{h}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{a}\left({k}−{h}\right)^{\mathrm{2}} +{k}−{x} \\ $$$$\:\:={a}^{\mathrm{3}} {x}^{\mathrm{4}} −\mathrm{4}{a}^{\mathrm{3}} {hx}^{\mathrm{3}} +\left[\mathrm{6}{a}^{\mathrm{3}} {h}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} \left({k}−{h}\right)\right]{x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:−\left[\mathrm{4}{a}^{\mathrm{3}} {h}^{\mathrm{3}} −+\mathrm{4}{a}^{\mathrm{2}} {h}\left({k}−{h}\right)+\mathrm{1}\right]{x} \\ $$$$\:+{a}^{\mathrm{3}} {h}^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{2}} \left({k}−{h}\right){h}^{\mathrm{2}} +{a}\left({k}−{h}\right)^{\mathrm{2}} +{k} \\ $$$${Also}\:{lets}\:{assume} \\ $$$${p}\left[{p}\left({x}\right)\right]−{x}={a}^{\mathrm{3}} \left[{x}^{\mathrm{2}} −\left(\mathrm{2}{ah}+\mathrm{1}\right){x}+{h}^{\mathrm{2}} +\frac{{k}}{{a}}\right]\left({x}−\gamma\right)\left({x}−\delta\right) \\ $$$$\:\:={a}^{\mathrm{3}} \left\{{x}^{\mathrm{4}} −\left(\gamma+\delta+\mathrm{2}{ah}+\mathrm{1}\right){x}^{\mathrm{3}} \right. \\ $$$$\:\:\:\:\:\:\:\:\:+\left[\gamma\delta+\left(\mathrm{2}{ah}+\mathrm{1}\right)\left(\gamma+\delta\right)+{h}^{\mathrm{2}} +\frac{{k}}{{a}}\right]{x}^{\mathrm{2}} \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:+\left({h}^{\mathrm{2}} +\frac{{k}}{{a}}\right)\gamma\delta\right\} \\ $$$${comparing}\:{the}\:{two}\:{expressions} \\ $$$${for}\:\:{p}\left[{p}\left({x}\right)\right]−{x}\:\:{we}\:{conclude} \\ $$$$\:\:\:\gamma+\delta\:=\:\mathrm{4}{h}−\mathrm{2}{ah}−\mathrm{1} \\ $$$$\:\gamma\delta\left({h}^{\mathrm{2}} +\frac{{k}}{{a}}\right)={a}^{\mathrm{3}} {h}^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{2}} \left({k}−{h}\right){h}^{\mathrm{2}} +{a}\left({k}−{h}\right)^{\mathrm{2}} +{k} \\ $$$${but}\:{from}\:\left({i}\right) \\ $$$$\:\:\:\:\:\mathrm{2}{h}+\frac{\mathrm{1}}{{a}}=\alpha+\beta \\ $$$$\:\:\:\:{h}^{\mathrm{2}} +\frac{{k}}{{a}}=\alpha\beta \\ $$$$..... \\ $$
Answered by perlman last updated on 31/May/19
![p(x)=(x−a)(x−b)+x p[p(x)]=(p(x)−a)(p(x)−b)+p(x) pp(x) −x=0 ==> (p(x)−a)(p(x)−b)+p(x)−x=0 =((x−a)(x−b)+x−a)((x−a)(x−b)+x−b)+(x−a)(x−b)=0 (x−a)(x−b+1)(x−b)(x−a+1)+(x−a)(x−b)=0 (x−a)(x−b)[(x−b+1)(x−a+1)+1]=0 let solve (x−b+1)(x−a+1)+1=0 x^2 −(b+a−2)x+(a−1)(b−1)+1=0 Δ=(b+a−2)^2 −4(ab−a−b+2)=(b^2 +a^2 +4+2ba−4a−4b)−4ab+4a+4b−8 =b^2 +a^2 −2ab−4=(b−a−2)(b−a+2) let b>a we can do this cause a#b ===>Δ≥0<==>b≥a+2 if b≥a+2 X_(1.2) =(((b+a−2)+_− (√((b−a−2)(b−a+2))))/2) if a<b<=a+2 X_(1.2) =(((b+a−2)+_− i(√((a+2−b)(b−a+2))))/2) solution are if b∈]a+2;+∞[ solutions are {b,a,(((b+a−2)+_− (√((b−a−2)(b−a+2))))/2)} if b∈]a;a+2[ solutions are {b,a,(((b+a−2)+_− i(√((b−a−2)(b−a+2))))/2)}](Q61282.png)
$${p}\left({x}\right)=\left({x}−{a}\right)\left({x}−{b}\right)+{x} \\ $$$${p}\left[{p}\left({x}\right)\right]=\left({p}\left({x}\right)−{a}\right)\left({p}\left({x}\right)−{b}\right)+{p}\left({x}\right) \\ $$$${pp}\left({x}\right)\:−{x}=\mathrm{0} \\ $$$$==>\:\left({p}\left({x}\right)−{a}\right)\left({p}\left({x}\right)−{b}\right)+{p}\left({x}\right)−{x}=\mathrm{0} \\ $$$$=\left(\left({x}−{a}\right)\left({x}−{b}\right)+{x}−{a}\right)\left(\left({x}−{a}\right)\left({x}−{b}\right)+{x}−{b}\right)+\left({x}−{a}\right)\left({x}−{b}\right)=\mathrm{0} \\ $$$$\left({x}−{a}\right)\left({x}−{b}+\mathrm{1}\right)\left({x}−{b}\right)\left({x}−{a}+\mathrm{1}\right)+\left({x}−{a}\right)\left({x}−{b}\right)=\mathrm{0} \\ $$$$\left({x}−{a}\right)\left({x}−{b}\right)\left[\left({x}−{b}+\mathrm{1}\right)\left({x}−{a}+\mathrm{1}\right)+\mathrm{1}\right]=\mathrm{0} \\ $$$${let}\:{solve}\:\left({x}−{b}+\mathrm{1}\right)\left({x}−{a}+\mathrm{1}\right)+\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\left({b}+{a}−\mathrm{2}\right){x}+\left({a}−\mathrm{1}\right)\left({b}−\mathrm{1}\right)+\mathrm{1}=\mathrm{0} \\ $$$$\Delta=\left({b}+{a}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}\left({ab}−{a}−{b}+\mathrm{2}\right)=\left({b}^{\mathrm{2}} +{a}^{\mathrm{2}} +\mathrm{4}+\mathrm{2}{ba}−\mathrm{4}{a}−\mathrm{4}{b}\right)−\mathrm{4}{ab}+\mathrm{4}{a}+\mathrm{4}{b}−\mathrm{8} \\ $$$$={b}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}{ab}−\mathrm{4}=\left({b}−{a}−\mathrm{2}\right)\left({b}−{a}+\mathrm{2}\right) \\ $$$${let}\:{b}>{a}\:{we}\:{can}\:{do}\:{this}\:{cause}\:{a}#{b} \\ $$$$===>\Delta\geqslant\mathrm{0}<==>{b}\geqslant{a}+\mathrm{2} \\ $$$${if}\:{b}\geqslant{a}+\mathrm{2} \\ $$$${X}_{\mathrm{1}.\mathrm{2}} =\frac{\left({b}+{a}−\mathrm{2}\right)\underset{−} {+}\sqrt{\left({b}−{a}−\mathrm{2}\right)\left({b}−{a}+\mathrm{2}\right)}}{\mathrm{2}} \\ $$$${if}\:{a}<{b}<={a}+\mathrm{2} \\ $$$${X}_{\mathrm{1}.\mathrm{2}} =\frac{\left({b}+{a}−\mathrm{2}\right)\underset{−} {+}{i}\sqrt{\left({a}+\mathrm{2}−{b}\right)\left({b}−{a}+\mathrm{2}\right)}}{\mathrm{2}} \\ $$$$\left.{solution}\:{are}\:{if}\:{b}\in\right]{a}+\mathrm{2};+\infty\left[\:{solutions}\:{are}\right. \\ $$$$\left\{{b},{a},\frac{\left({b}+{a}−\mathrm{2}\right)\underset{−} {+}\sqrt{\left({b}−{a}−\mathrm{2}\right)\left({b}−{a}+\mathrm{2}\right)}}{\mathrm{2}}\right\} \\ $$$$\left.{if}\:{b}\in\right]{a};{a}+\mathrm{2}\left[\:{solutions}\:{are}\right. \\ $$$$\left\{{b},{a},\frac{\left({b}+{a}−\mathrm{2}\right)\underset{−} {+}{i}\sqrt{\left({b}−{a}−\mathrm{2}\right)\left({b}−{a}+\mathrm{2}\right)}}{\mathrm{2}}\right\} \\ $$$$ \\ $$
Commented by alphaprime last updated on 31/May/19
Tanmay sir generalized and solution is pretty nice , but yours is valid in entire domain , But comment something on both the solutions , any remarks you wanna add , please ...
Commented by perlman last updated on 31/May/19
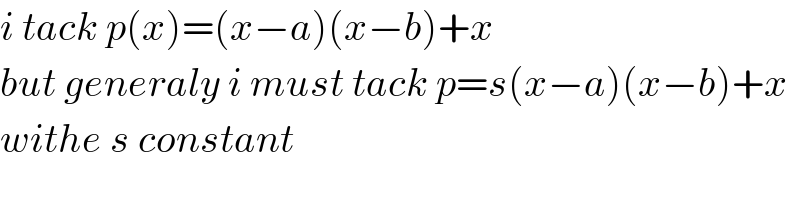
$${i}\:{tack}\:{p}\left({x}\right)=\left({x}−{a}\right)\left({x}−{b}\right)+{x} \\ $$$${but}\:{generaly}\:{i}\:{must}\:{tack}\:{p}={s}\left({x}−{a}\right)\left({x}−{b}\right)+{x} \\ $$$${withe}\:{s}\:{constant}\: \\ $$
Commented by alphaprime last updated on 31/May/19
You mentioned it finally , In Tanmay sir's solution It's dependent on the parameter A you've left , which you haven't taken as arbitrary constant, so does it affect his or your solution or neither ones ?! it's amazing
Answered by tanmay last updated on 31/May/19
![p(x)=A(x−α)(x−β)+x p[p(x)] =A[A(x−α)(x−β)+x−α](A(x−α)(x−β)+x−β]+ A(x−α)(x−β) +x−x so p[p(α)]=0 p[p(β)]=0 nxt part... p[p(x)] =A[(x−α){A(x−β)+1}][(x−β){A(x−α)+1}]+if A(x−α)(x−β) for other two root p[p(x)]=0 x−α=m x−β=n A[m(An+1)][n(Am+1]+Amn=0 (Amn+m)(Amn+n)+mn=0 A^2 (mn)^2 +Amn(m+n)+mn+mn=0 mn[A^2 (mn)+A(m+n)+2]=0 when A^2 (mn)+A(m+n)+2=0 A^2 (x−α)(x−β)+A(x−α+x−β)+2=0 A^2 (x^2 −xα−xβ+αβ)+2Ax−A(α+β)+2=0 x^2 (A^2 )+x(2A−A^2 α−A^2 β)+A^2 αβ−A(α+β)+2=0 (Ax+1)^2 +x(−A^2 α−A^2 β)+(A^2 αβ−Aα−Aβ+1)=0 (Ax+1)^2 −A^2 x(α+β)+Aα(Aβ−1)−(Aβ−1)=0 (Ax+1)^2 −A^2 x(α+β)+(Aα−1)(Aβ−1)=0 A^2 x^2 +2Ax+1−A^2 x(α+β)+(Aα−1)(Aβ−1)=0 A^2 x^2 −Ax(α+β−2)+(Aα−1)(Aβ−1)+1=0 x=((A(α+β−2)±(√(A^2 (α+β−2)^2 −4A^2 [(Aα−1)(Aβ−1)+1])))/(2A^2 )) x=((α+β−2±(√((α+β−2)^2 −4[(Aα−1)(Aβ−1)+1)))/(2A))](Q61285.png)
$${p}\left({x}\right)={A}\left({x}−\alpha\right)\left({x}−\beta\right)+{x} \\ $$$${p}\left[{p}\left({x}\right)\right] \\ $$$$={A}\left[{A}\left({x}−\alpha\right)\left({x}−\beta\right)+{x}−\alpha\right]\left({A}\left({x}−\alpha\right)\left({x}−\beta\right)+{x}−\beta\right]+ \\ $$$$\:\:{A}\left({x}−\alpha\right)\left({x}−\beta\right)\:+{x}−{x} \\ $$$${so}\: \\ $$$${p}\left[{p}\left(\alpha\right)\right]=\mathrm{0} \\ $$$${p}\left[{p}\left(\beta\right)\right]=\mathrm{0} \\ $$$${nxt}\:{part}... \\ $$$${p}\left[{p}\left({x}\right)\right] \\ $$$$={A}\left[\left({x}−\alpha\right)\left\{{A}\left({x}−\beta\right)+\mathrm{1}\right\}\right]\left[\left({x}−\beta\right)\left\{{A}\left({x}−\alpha\right)+\mathrm{1}\right\}\right]+{if} \\ $$$$\:\:\:\:{A}\left({x}−\alpha\right)\left({x}−\beta\right) \\ $$$${for}\:{other}\:{two}\:{root}\:{p}\left[{p}\left({x}\right)\right]=\mathrm{0} \\ $$$${x}−\alpha={m}\:\:\:\:{x}−\beta={n}\:\:\: \\ $$$${A}\left[{m}\left({An}+\mathrm{1}\right)\right]\left[{n}\left({Am}+\mathrm{1}\right]+{Amn}=\mathrm{0}\right. \\ $$$$\left({Amn}+{m}\right)\left({Amn}+{n}\right)+{mn}=\mathrm{0} \\ $$$${A}^{\mathrm{2}} \left({mn}\right)^{\mathrm{2}} +{Amn}\left({m}+{n}\right)+{mn}+{mn}=\mathrm{0} \\ $$$${mn}\left[{A}^{\mathrm{2}} \left({mn}\right)+{A}\left({m}+{n}\right)+\mathrm{2}\right]=\mathrm{0} \\ $$$${when}\:{A}^{\mathrm{2}} \left({mn}\right)+{A}\left({m}+{n}\right)+\mathrm{2}=\mathrm{0} \\ $$$${A}^{\mathrm{2}} \left({x}−\alpha\right)\left({x}−\beta\right)+{A}\left({x}−\alpha+{x}−\beta\right)+\mathrm{2}=\mathrm{0} \\ $$$${A}^{\mathrm{2}} \left({x}^{\mathrm{2}} −{x}\alpha−{x}\beta+\alpha\beta\right)+\mathrm{2}{Ax}−{A}\left(\alpha+\beta\right)+\mathrm{2}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left({A}^{\mathrm{2}} \right)+{x}\left(\mathrm{2}{A}−{A}^{\mathrm{2}} \alpha−{A}^{\mathrm{2}} \beta\right)+{A}^{\mathrm{2}} \alpha\beta−{A}\left(\alpha+\beta\right)+\mathrm{2}=\mathrm{0} \\ $$$$\left({Ax}+\mathrm{1}\right)^{\mathrm{2}} +{x}\left(−{A}^{\mathrm{2}} \alpha−{A}^{\mathrm{2}} \beta\right)+\left({A}^{\mathrm{2}} \alpha\beta−{A}\alpha−{A}\beta+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({Ax}+\mathrm{1}\right)^{\mathrm{2}} −{A}^{\mathrm{2}} {x}\left(\alpha+\beta\right)+{A}\alpha\left({A}\beta−\mathrm{1}\right)−\left({A}\beta−\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({Ax}+\mathrm{1}\right)^{\mathrm{2}} −{A}^{\mathrm{2}} {x}\left(\alpha+\beta\right)+\left({A}\alpha−\mathrm{1}\right)\left({A}\beta−\mathrm{1}\right)=\mathrm{0} \\ $$$${A}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{2}{Ax}+\mathrm{1}−{A}^{\mathrm{2}} {x}\left(\alpha+\beta\right)+\left({A}\alpha−\mathrm{1}\right)\left({A}\beta−\mathrm{1}\right)=\mathrm{0} \\ $$$${A}^{\mathrm{2}} {x}^{\mathrm{2}} −{Ax}\left(\alpha+\beta−\mathrm{2}\right)+\left({A}\alpha−\mathrm{1}\right)\left({A}\beta−\mathrm{1}\right)+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{{A}\left(\alpha+\beta−\mathrm{2}\right)\pm\sqrt{{A}^{\mathrm{2}} \left(\alpha+\beta−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}{A}^{\mathrm{2}} \left[\left({A}\alpha−\mathrm{1}\right)\left({A}\beta−\mathrm{1}\right)+\mathrm{1}\right]}}{\mathrm{2}{A}^{\mathrm{2}} } \\ $$$${x}=\frac{\alpha+\beta−\mathrm{2}\pm\sqrt{\left(\alpha+\beta−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}\left[\left({A}\alpha−\mathrm{1}\right)\left({A}\beta−\mathrm{1}\right)+\mathrm{1}\right.}}{\mathrm{2}{A}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by alphaprime last updated on 31/May/19
Very Nice cognizant
Commented by tanmay last updated on 31/May/19

$${thank}\:{you}\:{sir}... \\ $$
Commented by alphaprime last updated on 31/May/19
Question no.61211 , I seriously need your help sir , I can't even come on telegram due to issues, I'm seeking intense help , I don't expect much but there's a hope , Mjs sir is with me in the workspace and has promised to provide solution till Monday, I need you and other intellectuals to join him and resolve the system Indeed help me out please sir ��
Commented by ajfour last updated on 31/May/19

$${We}\:{too}\:{are}\:{glad}\:{to}\:{have}\:{you}\:{here} \\ $$$${on}\:{the}\:{forum}\:{Sir}.\:{Your}\:{questions} \\ $$$${are}\:{precious}. \\ $$
Commented by alphaprime last updated on 31/May/19
Sir I'm welcoming you in my workspace and please don't disappoint me , I'll love to notice presence of higher intellectual faculty , Just provide me your email ��
