Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 61273 by alphaprime last updated on 31/May/19

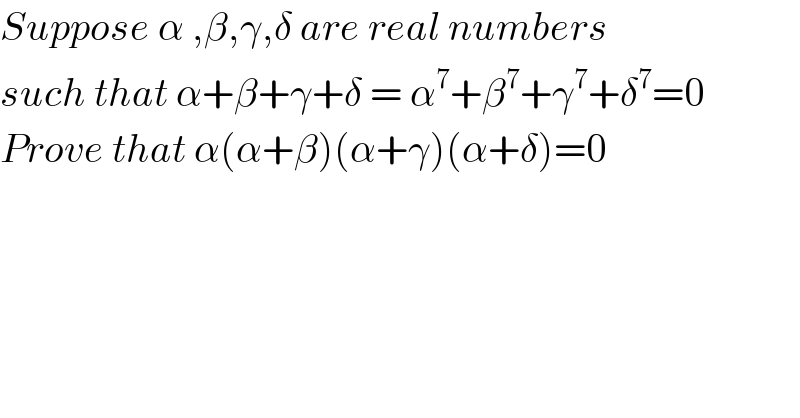
Suppose α ,β,γ,δ are real numbers such that α+β+γ+δ = α^7 +β^7 +γ^7 +δ^7 =0 Prove that α(α+β)(α+γ)(α+δ)=0

$${Suppose}\:\alpha\:,\beta,\gamma,\delta\:{are}\:{real}\:{numbers} \\ $$$${such}\:{that}\:\alpha+\beta+\gamma+\delta\:=\:\alpha^{\mathrm{7}} +\beta^{\mathrm{7}} +\gamma^{\mathrm{7}} +\delta^{\mathrm{7}} =\mathrm{0} \\ $$$${Prove}\:{that}\:\alpha\left(\alpha+\beta\right)\left(\alpha+\gamma\right)\left(\alpha+\delta\right)=\mathrm{0} \\ $$

Commented by Rasheed.Sindhi last updated on 31/May/19

α+β+γ+δ = α^7 +β^7 +γ^7 +δ^7 =0 It can be proved that any two of four have same value and remaining two are additive inverse of the mentioned two numbers(Only possibility) So Let α=β=k ,γ=δ=−k α+β+γ+δ = α^7 +β^7 +γ^7 +δ^7 =0 ⇒ k+k−k−k=k^7 +k^7 −k^7 −k^7 =0 α(α+β)(α+γ)(α+δ) =k(k+k)(k−k)(k−) =k.2k.0.0=0 Proved

$$\:\:\:\alpha+\beta+\gamma+\delta\:=\:\alpha^{\mathrm{7}} +\beta^{\mathrm{7}} +\gamma^{\mathrm{7}} +\delta^{\mathrm{7}} =\mathrm{0} \\ $$$$\mathrm{It}\:\mathrm{can}\:\mathrm{be}\:\mathrm{proved}\:\mathrm{that}\:\mathrm{any}\:\mathrm{two}\:\mathrm{of} \\ $$$$\mathrm{four}\:\mathrm{have}\:\mathrm{same}\:\mathrm{value}\:\mathrm{and}\:\mathrm{remaining} \\ $$$$\mathrm{two}\:\mathrm{are}\:\mathrm{additive}\:\mathrm{inverse}\:\mathrm{of}\:\mathrm{the}\:\mathrm{mentioned} \\ $$$$\mathrm{two}\:\mathrm{numbers}\left(\mathrm{Only}\:\mathrm{possibility}\right) \\ $$$$\mathrm{So} \\ $$$$\mathrm{Let}\:\:\alpha=\beta=\mathrm{k}\:,\gamma=\delta=−\mathrm{k} \\ $$$$\:\:\:\alpha+\beta+\gamma+\delta\:=\:\alpha^{\mathrm{7}} +\beta^{\mathrm{7}} +\gamma^{\mathrm{7}} +\delta^{\mathrm{7}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\Rightarrow\:\mathrm{k}+\mathrm{k}−\mathrm{k}−\mathrm{k}=\mathrm{k}^{\mathrm{7}} +\mathrm{k}^{\mathrm{7}} −\mathrm{k}^{\mathrm{7}} −\mathrm{k}^{\mathrm{7}} =\mathrm{0} \\ $$$$\:\alpha\left(\alpha+\beta\right)\left(\alpha+\gamma\right)\left(\alpha+\delta\right) \\ $$$$\:\:\:\:\:\:=\mathrm{k}\left(\mathrm{k}+\mathrm{k}\right)\left(\mathrm{k}−\mathrm{k}\right)\left(\mathrm{k}−\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{k}.\mathrm{2k}.\mathrm{0}.\mathrm{0}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\mathrm{Proved} \\ $$$$ \\ $$

Commented by alphaprime last updated on 01/Jun/19

Could it have been better please?!

Answered by Rasheed.Sindhi last updated on 02/Jun/19

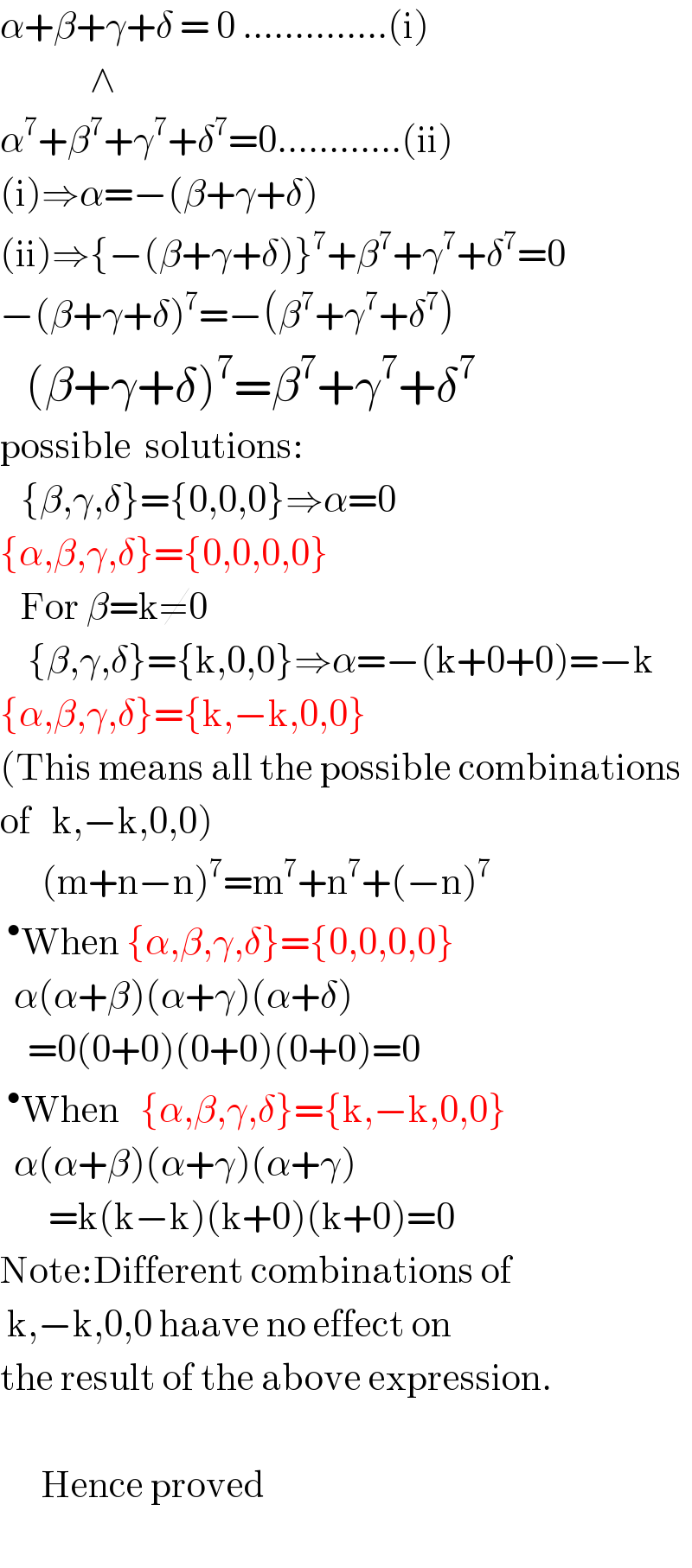
α+β+γ+δ = 0 ..............(i) ∧ α^7 +β^7 +γ^7 +δ^7 =0............(ii) (i)⇒α=−(β+γ+δ) (ii)⇒{−(β+γ+δ)}^7 +β^7 +γ^7 +δ^7 =0 −(β+γ+δ)^7 =−(β^7 +γ^7 +δ^7 ) (β+γ+δ)^7 =β^7 +γ^7 +δ^7 possible solutions: {β,γ,δ}={0,0,0}⇒α=0 {α,β,γ,δ}={0,0,0,0} For β=k≠0 {β,γ,δ}={k,0,0}⇒α=−(k+0+0)=−k {α,β,γ,δ}={k,−k,0,0} (This means all the possible combinations of k,−k,0,0) (m+n−n)^7 =m^7 +n^7 +(−n)^7 ^• When {α,β,γ,δ}={0,0,0,0} α(α+β)(α+γ)(α+δ) =0(0+0)(0+0)(0+0)=0 ^• When {α,β,γ,δ}={k,−k,0,0} α(α+β)(α+γ)(α+γ) =k(k−k)(k+0)(k+0)=0 Note:Different combinations of k,−k,0,0 haave no effect on the result of the above expression. Hence proved

$$\alpha+\beta+\gamma+\delta\:=\:\mathrm{0}\:..............\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\wedge \\ $$$$\alpha^{\mathrm{7}} +\beta^{\mathrm{7}} +\gamma^{\mathrm{7}} +\delta^{\mathrm{7}} =\mathrm{0}............\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{i}\right)\Rightarrow\alpha=−\left(\beta+\gamma+\delta\right) \\ $$$$\left(\mathrm{ii}\right)\Rightarrow\left\{−\left(\beta+\gamma+\delta\right)\right\}^{\mathrm{7}} +\beta^{\mathrm{7}} +\gamma^{\mathrm{7}} +\delta^{\mathrm{7}} =\mathrm{0} \\ $$$$−\left(\beta+\gamma+\delta\right)^{\mathrm{7}} =−\left(\beta^{\mathrm{7}} +\gamma^{\mathrm{7}} +\delta^{\mathrm{7}} \right) \\ $$$$\:\:\:\left(\beta+\gamma+\delta\right)^{\mathrm{7}} =\beta^{\mathrm{7}} +\gamma^{\mathrm{7}} +\delta^{\mathrm{7}} \\ $$$$\mathrm{possible}\:\:\mathrm{solutions}: \\ $$$$\:\:\:\left\{\beta,\gamma,\delta\right\}=\left\{\mathrm{0},\mathrm{0},\mathrm{0}\right\}\Rightarrow\alpha=\mathrm{0} \\ $$$$\left\{\alpha,\beta,\gamma,\delta\right\}=\left\{\mathrm{0},\mathrm{0},\mathrm{0},\mathrm{0}\right\} \\ $$$$\:\:\:\mathrm{For}\:\beta=\mathrm{k}\neq\mathrm{0} \\ $$$$\:\:\:\:\left\{\beta,\gamma,\delta\right\}=\left\{\mathrm{k},\mathrm{0},\mathrm{0}\right\}\Rightarrow\alpha=−\left(\mathrm{k}+\mathrm{0}+\mathrm{0}\right)=−\mathrm{k} \\ $$$$\left\{\alpha,\beta,\gamma,\delta\right\}=\left\{\mathrm{k},−\mathrm{k},\mathrm{0},\mathrm{0}\right\} \\ $$$$\left(\mathrm{This}\:\mathrm{means}\:\mathrm{all}\:\mathrm{the}\:\mathrm{possible}\:\mathrm{combinations}\right. \\ $$$$\left.\mathrm{of}\:\:\:\mathrm{k},−\mathrm{k},\mathrm{0},\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\left(\mathrm{m}+\mathrm{n}−\mathrm{n}\right)^{\mathrm{7}} =\mathrm{m}^{\mathrm{7}} +\mathrm{n}^{\mathrm{7}} +\left(−\mathrm{n}\right)^{\mathrm{7}} \\ $$$$\:^{\bullet} \mathrm{When}\:\left\{\alpha,\beta,\gamma,\delta\right\}=\left\{\mathrm{0},\mathrm{0},\mathrm{0},\mathrm{0}\right\} \\ $$$$\:\:\alpha\left(\alpha+\beta\right)\left(\alpha+\gamma\right)\left(\alpha+\delta\right) \\ $$$$\:\:\:\:=\mathrm{0}\left(\mathrm{0}+\mathrm{0}\right)\left(\mathrm{0}+\mathrm{0}\right)\left(\mathrm{0}+\mathrm{0}\right)=\mathrm{0} \\ $$$$\:^{\bullet} \mathrm{When}\:\:\:\left\{\alpha,\beta,\gamma,\delta\right\}=\left\{\mathrm{k},−\mathrm{k},\mathrm{0},\mathrm{0}\right\} \\ $$$$\:\:\alpha\left(\alpha+\beta\right)\left(\alpha+\gamma\right)\left(\alpha+\gamma\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{k}\left(\mathrm{k}−\mathrm{k}\right)\left(\mathrm{k}+\mathrm{0}\right)\left(\mathrm{k}+\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{Note}:\mathrm{Different}\:\mathrm{combinations}\:\mathrm{of} \\ $$$$\:\mathrm{k},−\mathrm{k},\mathrm{0},\mathrm{0}\:\mathrm{haave}\:\mathrm{no}\:\mathrm{effect}\:\mathrm{on} \\ $$$$\mathrm{the}\:\mathrm{result}\:\mathrm{of}\:\mathrm{the}\:\mathrm{above}\:\mathrm{expression}. \\ $$$$ \\ $$$$\:\:\:\:\:\:\mathrm{Hence}\:\mathrm{proved} \\ $$$$\:\: \\ $$

Commented by alphaprime last updated on 02/Jun/19

Thank you gentlemen :)

Commented by Rasheed.Sindhi last updated on 02/Jun/19

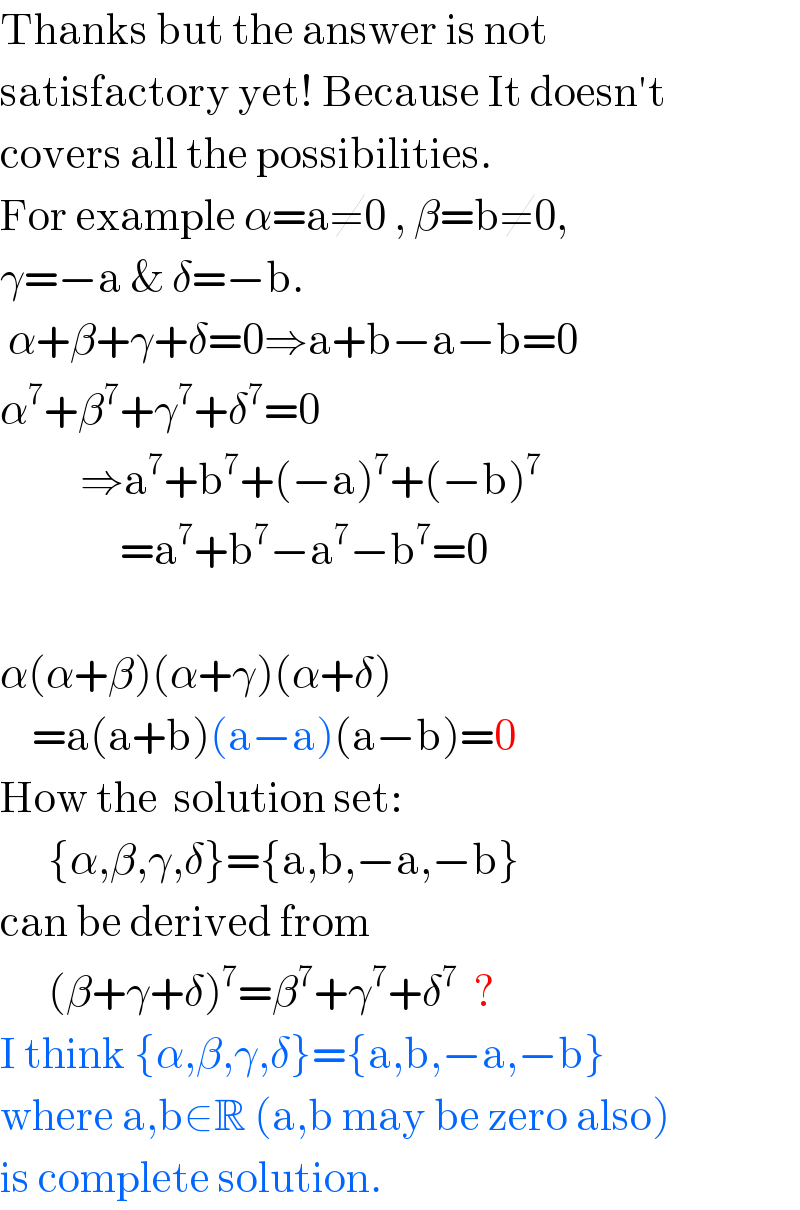
Thanks but the answer is not satisfactory yet! Because It doesn′t covers all the possibilities. For example α=a≠0 , β=b≠0, γ=−a & δ=−b. α+β+γ+δ=0⇒a+b−a−b=0 α^7 +β^7 +γ^7 +δ^7 =0 ⇒a^7 +b^7 +(−a)^7 +(−b)^7 =a^7 +b^7 −a^7 −b^7 =0 α(α+β)(α+γ)(α+δ) =a(a+b)(a−a)(a−b)=0 How the solution set: {α,β,γ,δ}={a,b,−a,−b} can be derived from (β+γ+δ)^7 =β^7 +γ^7 +δ^7 ? I think {α,β,γ,δ}={a,b,−a,−b} where a,b∈R (a,b may be zero also) is complete solution.

$$\mathrm{Thanks}\:\mathrm{but}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{satisfactory}\:\mathrm{yet}!\:\mathrm{Because}\:\mathrm{It}\:\mathrm{doesn}'\mathrm{t} \\ $$$$\mathrm{covers}\:\mathrm{all}\:\mathrm{the}\:\mathrm{possibilities}. \\ $$$$\mathrm{For}\:\mathrm{example}\:\alpha=\mathrm{a}\neq\mathrm{0}\:,\:\beta=\mathrm{b}\neq\mathrm{0}, \\ $$$$\gamma=−\mathrm{a}\:\&\:\delta=−\mathrm{b}. \\ $$$$\:\alpha+\beta+\gamma+\delta=\mathrm{0}\Rightarrow\mathrm{a}+\mathrm{b}−\mathrm{a}−\mathrm{b}=\mathrm{0} \\ $$$$\alpha^{\mathrm{7}} +\beta^{\mathrm{7}} +\gamma^{\mathrm{7}} +\delta^{\mathrm{7}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{a}^{\mathrm{7}} +\mathrm{b}^{\mathrm{7}} +\left(−\mathrm{a}\right)^{\mathrm{7}} +\left(−\mathrm{b}\right)^{\mathrm{7}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{a}^{\mathrm{7}} +\mathrm{b}^{\mathrm{7}} −\mathrm{a}^{\mathrm{7}} −\mathrm{b}^{\mathrm{7}} =\mathrm{0} \\ $$$$ \\ $$$$\alpha\left(\alpha+\beta\right)\left(\alpha+\gamma\right)\left(\alpha+\delta\right) \\ $$$$\:\:\:\:=\mathrm{a}\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{a}−\mathrm{a}\right)\left(\mathrm{a}−\mathrm{b}\right)=\mathrm{0} \\ $$$$\mathrm{How}\:\mathrm{the}\:\:\mathrm{solution}\:\mathrm{set}: \\ $$$$\:\:\:\:\:\:\left\{\alpha,\beta,\gamma,\delta\right\}=\left\{\mathrm{a},\mathrm{b},−\mathrm{a},−\mathrm{b}\right\} \\ $$$$\mathrm{can}\:\mathrm{be}\:\mathrm{derived}\:\mathrm{from} \\ $$$$\:\:\:\:\:\:\left(\beta+\gamma+\delta\right)^{\mathrm{7}} =\beta^{\mathrm{7}} +\gamma^{\mathrm{7}} +\delta^{\mathrm{7}} \:\:? \\ $$$$\mathrm{I}\:\mathrm{think}\:\left\{\alpha,\beta,\gamma,\delta\right\}=\left\{\mathrm{a},\mathrm{b},−\mathrm{a},−\mathrm{b}\right\} \\ $$$$\mathrm{where}\:\mathrm{a},\mathrm{b}\in\mathbb{R}\:\left(\mathrm{a},\mathrm{b}\:\mathrm{may}\:\mathrm{be}\:\mathrm{zero}\:\mathrm{also}\right) \\ $$$$\mathrm{is}\:\mathrm{complete}\:\mathrm{solution}. \\ $$

Answered by Rasheed.Sindhi last updated on 03/Jun/19

α+β+γ+δ =0.............(i) ∧ α^7 +β^7 +γ^7 +δ^7 =0..........(ii) ⌣⌢⌣⌢⌣⌢⌣⌢⌣⌢^(−) Let α=a , β=b where a,b∈R (i)⇒γ+δ=−a−b.............(iii) (ii)⇒γ^7 +δ^7 =−a^7 −b^7 .......(iv) (iii) & (iv) have only two real solutions (See the answer & comments of sir MJS to Q#61470) and they are γ=−a ∧ δ=−b OR γ=−b ∧ δ=−a Hence the general solution to α+β+γ+δ = α^7 +β^7 +γ^7 +δ^7 =0 is {α,β,γ,δ}={a,b,−a,−b} for real α,β,γ,δ. To prove α(α+β)(α+γ)(α+δ)=0 α(α+β)(α+γ)(α+δ) =a(a+b)(a−a)(a−b) =a(a+b)(0)(a−b)=0

$$\alpha+\beta+\gamma+\delta\:=\mathrm{0}.............\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\wedge \\ $$$$\alpha^{\mathrm{7}} +\beta^{\mathrm{7}} +\gamma^{\mathrm{7}} +\delta^{\mathrm{7}} =\mathrm{0}..........\left(\mathrm{ii}\right) \\ $$$$\overline {\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown} \\ $$$$\mathrm{Let}\:\alpha=\mathrm{a}\:,\:\beta=\mathrm{b}\:\mathrm{where}\:\mathrm{a},\mathrm{b}\in\mathbb{R} \\ $$$$\left(\mathrm{i}\right)\Rightarrow\gamma+\delta=−\mathrm{a}−\mathrm{b}.............\left(\mathrm{iii}\right) \\ $$$$\left(\mathrm{ii}\right)\Rightarrow\gamma^{\mathrm{7}} +\delta^{\mathrm{7}} =−\mathrm{a}^{\mathrm{7}} −\mathrm{b}^{\mathrm{7}} .......\left(\mathrm{iv}\right) \\ $$$$\left(\mathrm{iii}\right)\:\&\:\left(\mathrm{iv}\right)\:\mathrm{have}\:\mathrm{only}\:\mathrm{two}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$\left(\mathrm{See}\:\mathrm{the}\:\mathrm{answer}\:\&\:\mathrm{comments}\:\mathrm{of}\:\mathrm{sir}\right. \\ $$$$\left.\:\mathrm{MJS}\:\mathrm{to}\:\mathrm{Q}#\mathrm{61470}\right)\:\mathrm{and}\:\mathrm{they}\:\mathrm{are}\: \\ $$$$\:\:\:\:\:\:\:\:\:\gamma=−\mathrm{a}\:\wedge\:\delta=−\mathrm{b} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{OR} \\ $$$$\:\:\:\:\:\:\:\:\:\gamma=−\mathrm{b}\:\wedge\:\delta=−\mathrm{a} \\ $$$$\mathcal{H}\mathrm{ence}\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{to} \\ $$$$\alpha+\beta+\gamma+\delta\:=\:\alpha^{\mathrm{7}} +\beta^{\mathrm{7}} +\gamma^{\mathrm{7}} +\delta^{\mathrm{7}} =\mathrm{0} \\ $$$$\mathrm{is}\:\left\{\alpha,\beta,\gamma,\delta\right\}=\left\{\mathrm{a},\mathrm{b},−\mathrm{a},−\mathrm{b}\right\}\:\mathrm{for}\:\mathrm{real} \\ $$$$\alpha,\beta,\gamma,\delta. \\ $$$$\: \\ $$$$\mathrm{To}\:\mathrm{prove}\:\alpha\left(\alpha+\beta\right)\left(\alpha+\gamma\right)\left(\alpha+\delta\right)=\mathrm{0} \\ $$$$\:\:\:\alpha\left(\alpha+\beta\right)\left(\alpha+\gamma\right)\left(\alpha+\delta\right) \\ $$$$\:\:\:\:\:=\mathrm{a}\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{a}−\mathrm{a}\right)\left(\mathrm{a}−\mathrm{b}\right) \\ $$$$\:\:\:\:\:=\mathrm{a}\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{0}\right)\left(\mathrm{a}−\mathrm{b}\right)=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com