Question Number 61303 by mr W last updated on 31/May/19
Commented by mr W last updated on 31/May/19
$${A}\:{small}\:{sphere}\:\left({say}\:{the}\:{moon}\right)\:{moves} \\ $$$${around}\:{a}\:{big}\:{sphere}\:\left({say}\:{the}\:{earth}\right)\:{in} \\ $$$${a}\:{circular}\:{track}.\:{A}\:{point}\:{source}\:\left({say}\right. \\ $$$$\left.{the}\:{sun}\right)\:{is}\:{at}\:{a}\:{distance}\:{e}\:{from}\:{the} \\ $$$${center}\:{of}\:{the}\:{big}\:{sphere}. \\ $$$${Find}\:{the}\:{area}\:{of}\:{shadow}\:{of}\:{the}\:{small} \\ $$$${sphere}\:{on}\:{the}\:{surface}\:{of}\:{the}\:{big} \\ $$$${sphere}\:{in}\:{terms}\:{of}\:\alpha.\:{Find}\:{the} \\ $$$${maximum}\:{shadow}\:{area}. \\ $$$${We}\:{only}\:{need}\:{to}\:{treat}\:{the}\:{case}\:{that} \\ $$$${the}\:{shadow}\:{is}\:{completely}\:{on}\:{the}\:{surface} \\ $$$${of}\:{the}\:{big}\:{sphere}. \\ $$
Commented by ajfour last updated on 02/Jun/19
$${Plan}\:{Only}\:\left({difficult}\:{to}\:{obtain}\right. \\ $$$$\left.\:{an}\:{answer}\:{this}\:{way}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${F}\left({e},\mathrm{0},\mathrm{0}\right) \\ $$$${T}\left({d}\mathrm{cos}\:\alpha+{r}\mathrm{sin}\:\phi\mathrm{cos}\:\psi,{r}\mathrm{sin}\:\phi\mathrm{sin}\:\psi,{d}\mathrm{sin}\:\alpha+{r}\mathrm{cos}\:\phi\right) \\ $$$${let}\:\:\angle{POG}=\delta \\ $$$${P}\:\left({R}\mathrm{cos}\:\delta\mathrm{cos}\:\theta,{R}\mathrm{cos}\:\delta\mathrm{sin}\:\theta,{R}\mathrm{sin}\:\delta\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${FT}^{\mathrm{2}} ={CF}^{\mathrm{2}} +{CT}^{\mathrm{2}} \\ $$$$\left({e}−{d}\mathrm{cos}\:\alpha−{r}\mathrm{sin}\:\phi\mathrm{cos}\:\psi\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \phi\mathrm{sin}\:^{\mathrm{2}} \psi \\ $$$$\:\:\:\:\:+\left({d}\mathrm{sin}\:\alpha+{r}\mathrm{cos}\:\phi\right)^{\mathrm{2}} +\boldsymbol{{r}}^{\mathrm{2}} = \\ $$$$\:\left({e}−{d}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{d}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha\:\:\:...\left({i}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${As}\:{FTP}\:{is}\:{straight}: \\ $$$$\frac{{R}\mathrm{cos}\:\delta\mathrm{cos}\:\theta−{e}}{{d}\mathrm{cos}\:\alpha+{r}\mathrm{sin}\:\phi\mathrm{cos}\:\psi−{e}}=\frac{{R}\mathrm{cos}\:\delta\mathrm{sin}\:\theta}{{r}\mathrm{sin}\:\phi\mathrm{sin}\:\psi} \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{{R}\mathrm{sin}\:\delta}{{d}\mathrm{sin}\:\alpha+{r}\mathrm{cos}\:\phi}\:\:\:\:..\left({ii}\right),\:\left({iii}\right) \\ $$$${from}\:\left({i}\right),\:\left({ii}\right),\:\left({iii}\right) \\ $$$${we}\:{find}\:\theta={f}\left(\delta\right)\:{eliminating} \\ $$$$\phi\:{and}\:\psi\:{from}\:{them}. \\ $$$${A}=\mathrm{2}\int_{\delta_{{min}} } ^{\:\:\delta_{{max}} } \left({R}\mathrm{cos}\:\delta\right)\theta\left({Rd}\delta\right) \\ $$$${for}\:{obtaining}\:\delta_{{min}} ,\:\delta_{{max}} \:\:{we}\:{take} \\ $$$$\theta=\mathrm{0},\:\psi=\mathrm{0} \\ $$$$\Rightarrow\:\frac{{R}\mathrm{cos}\:\delta−{e}}{{d}\mathrm{cos}\:\alpha+{r}\mathrm{sin}\:\phi−{e}}=\frac{{R}\mathrm{sin}\:\delta}{{d}\mathrm{sin}\:\alpha+{r}\mathrm{cos}\:\phi} \\ $$$${for}\:\:\phi_{{min}} \:{and}\:\phi_{{max}} \\ $$$$\left({e}−{d}\mathrm{cos}\:\alpha−{r}\mathrm{sin}\:\phi\right)^{\mathrm{2}} +\left({d}\mathrm{sin}\:\alpha+{r}\mathrm{cos}\:\phi\right)^{\mathrm{2}} \\ $$$$\:\:\:+{r}^{\mathrm{2}} \:=\left({e}−{d}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{d}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha \\ $$$$\Rightarrow\:\left({e}−{d}\mathrm{cos}\:\alpha\right)\mathrm{sin}\:\phi−{d}\mathrm{sin}\:\alpha\mathrm{cos}\:\phi={r}\: \\ $$$$\:\:\mathrm{sin}\:\left(\phi+\mathrm{tan}^{−\mathrm{1}} \frac{{d}\mathrm{sin}\:\alpha}{{e}−{d}\mathrm{cos}\:\alpha}\right)=\frac{{r}}{\sqrt{\left({e}−{d}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{d}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha}} \\ $$$$\Rightarrow\:\phi_{\mathrm{1}} =\mathrm{sin}^{−\mathrm{1}} \left(\frac{{r}}{\sqrt{\left({e}−{d}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{d}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{tan}^{−\mathrm{1}} \frac{{d}\mathrm{sin}\:\alpha}{{e}−{d}\mathrm{cos}\:\alpha} \\ $$$$\&\:\:\phi_{\mathrm{2}} =\:\pi−\mathrm{sin}^{−\mathrm{1}} \left(\frac{{r}}{\sqrt{\left({e}−{d}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{d}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{tan}^{−\mathrm{1}} \frac{{d}\mathrm{sin}\:\alpha}{{e}−{d}\mathrm{cos}\:\alpha} \\ $$$${We}\:{then}\:{obtain}\:\delta_{{min}} \:{and}\:\delta_{{max}} \\ $$$${from}\:{upper}\:{eq}. \\ $$$$..... \\ $$
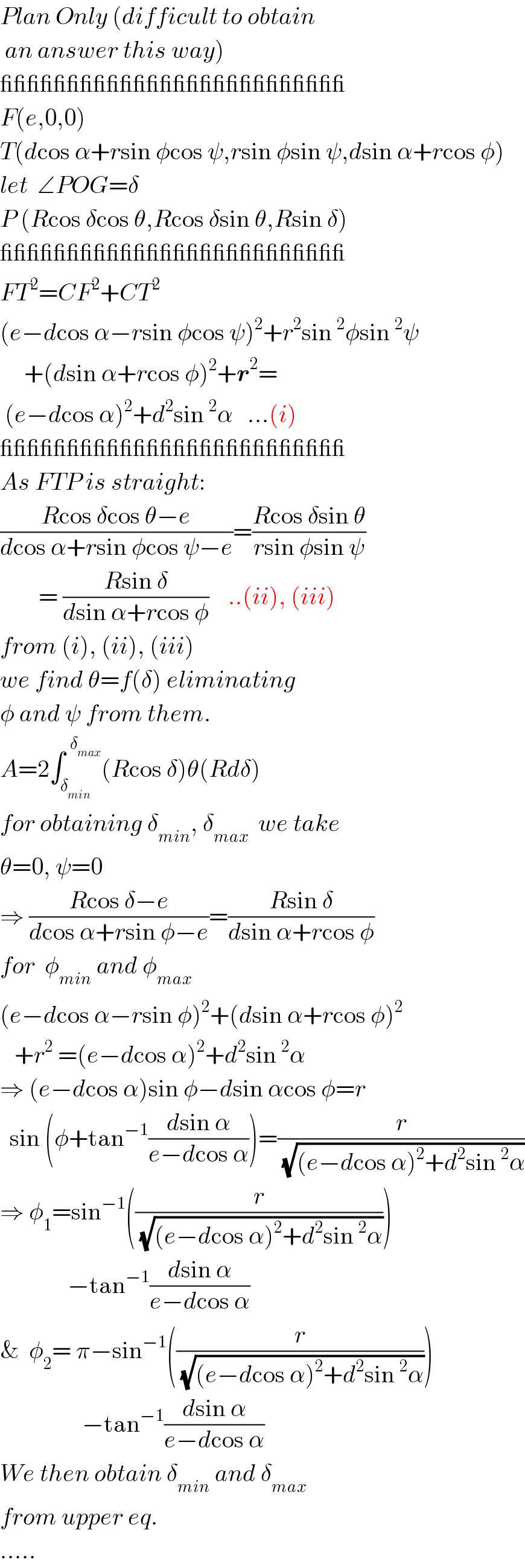
Commented by mr W last updated on 01/Jun/19
$${thanks}\:{for}\:{trying}\:{sir}!\:{i}\:{have}\:{not}\:{got} \\ $$$${a}\:{solution}.\:{but}\:{your}\:{method}\:{would}\:{be} \\ $$$${that}\:{what}\:{i}\:{had}\:{also}\:{used}.\:{but}\:{on}\:{the} \\ $$$${other}\:{side}\:{i}\:{think}\:{there}\:{should}\:{be}\:{an} \\ $$$${other}\:{maybe}\:{easier}\:{way}.\:{i}'{ll}\:{try}\:{it} \\ $$$${later}. \\ $$
Answered by ajfour last updated on 02/Jun/19
Answered by mr W last updated on 02/Jun/19
Commented by mr W last updated on 02/Jun/19
$${the}\:{light}\:{rays}\:{form}\:{a}\:{right}\:{circular} \\ $$$${cone}.\:{our}\:{task}\:{is}\:{to}\:{determine} \\ $$$${the}\:{intersection}\:{from} \\ $$$${this}\:{cone}\:{and}\:{the}\:{big}\:{sphere}. \\ $$$${to}\:{simplify}\:{the}\:{calcultion}\:{i}\:{select}\:{the} \\ $$$${source}\:{S}\:{as}\:{origin}\:{and}\:{SM}\:{as}\:{x}−{axis}. \\ $$$${the}\:{shape}\:{of}\:{cone}\:{is}\:{described}\:{by}\:{the} \\ $$$${angle}\:\beta. \\ $$$${the}\:{position}\:{of}\:{the}\:{big}\:{sphere}\:{is} \\ $$$${described}\:{by}\:{h}\:{and}\:{k}. \\ $$$${SO}={e},\:{OM}={d} \\ $$$${SM}=\sqrt{\left({e}−{d}\:\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +\left({d}\:\mathrm{sin}\:\alpha\right)^{\mathrm{2}} } \\ $$$$=\sqrt{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha} \\ $$$$\mathrm{sin}\:\beta=\frac{{r}}{\sqrt{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha}} \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{\sqrt{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha}} \\ $$$$\mathrm{tan}\:\beta=\frac{{r}}{\sqrt{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −{r}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha}}={m}\:\left({say}\right) \\ $$$$\frac{{k}}{{d}\:\mathrm{sin}\:\alpha}=\frac{{e}}{{SM}} \\ $$$$\Rightarrow{k}=\frac{{ed}\:\mathrm{sin}\:\alpha}{\sqrt{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha}} \\ $$$${h}=\sqrt{{e}^{\mathrm{2}} −{k}^{\mathrm{2}} }=\sqrt{{e}^{\mathrm{2}} −\frac{{e}^{\mathrm{2}} {d}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\alpha}{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha}} \\ $$$$\Rightarrow{h}=\frac{{e}\left({e}−{d}\:\mathrm{cos}\:\alpha\right)}{\sqrt{{e}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{ed}\:\mathrm{cos}\:\alpha}} \\ $$$$ \\ $$$${condition}\:{such}\:{that}\:{the}\:{shadow}\:{is} \\ $$$${completely}\:{on}\:{the}\:{big}\:{sphere}\:{is} \\ $$$$\mathrm{sin}\:\beta=\frac{{R}−\frac{{k}}{\mathrm{cos}\:\beta}}{{h}−{k}\:\mathrm{tan}\:\beta}=\frac{{R}\:\mathrm{cos}\:\beta−{k}}{{h}\:\mathrm{cos}\:\beta−{k}\:\mathrm{sin}\:\beta} \\ $$
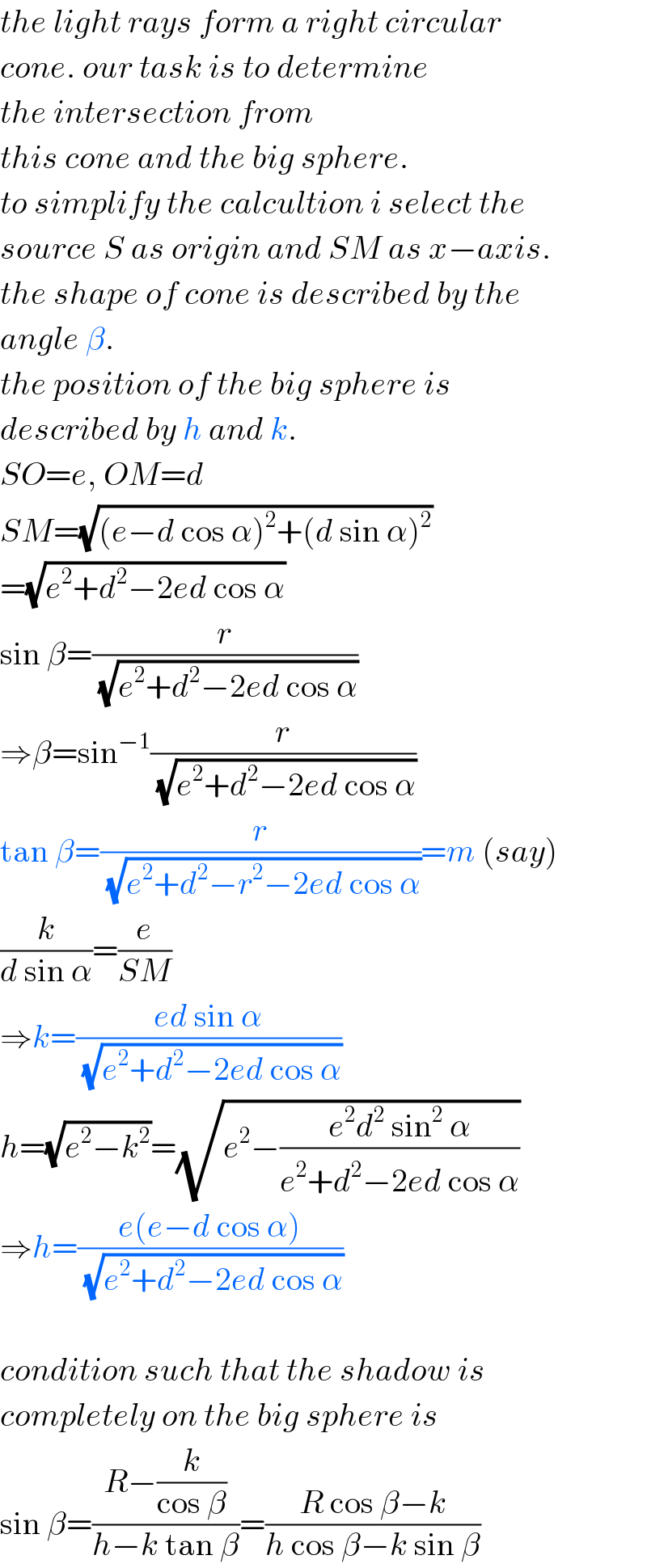
Commented by mr W last updated on 02/Jun/19
Commented by mr W last updated on 03/Jun/19
![eqn. of cone: x=((√(y^2 +z^2 ))/(tan β))=((√(y^2 +z^2 ))/m) or y^2 =m^2 x^2 −z^2 eqn. of sphere: (x−h)^2 +y^2 +(z+k)^2 =R^2 intersection of cone and sphere: (x−h)^2 +m^2 x^2 −z^2 +(z+k)^2 =R^2 ⇒(1+m^2 )x^2 −2hx+2kz+(h^2 +k^2 −R^2 )=0 ...(i) (this is a parabola in xz−plane) at θ: let ρ=R−Δh x=h−ρ cos θ z=−k+ρ sin θ put this into (i): (1+m^2 )[h−ρ cos θ]^2 −2h[h−ρ cos θ]+2k[−k+ρ sin θ]+(h^2 +k^2 −R^2 )=0 (1+m^2 )cos^2 θ ρ^2 −2(m^2 h cos θ−k sin θ)ρ+(m^2 h^2 −k^2 −R^2 )=0 ⇒ρ=(((m^2 h cos θ−k sin θ)+(√(m^4 h^2 cos^2 θ+k^2 sin^2 θ−2m^2 hk sin θ cos θ−(1+m^2 )cos^2 θ(m^2 h^2 −k^2 −R^2 ))))/((1+m^2 )cos^2 θ)) (two intersections, we take + for the left one) ⇒ρ=R cos ϕ=(((m^2 h cos θ−k sin θ)+(√(k^2 +[(1+m^2 )R^2 −m^2 (h^2 −k^2 )]cos^2 θ−m^2 hk sin 2θ)))/((1+m^2 )cos^2 θ)) ⇒ϕ=cos^(−1) {(((m^2 h cos θ−k sin θ)+(√(k^2 +[(1+m^2 )R^2 −m^2 (h^2 −k^2 )]cos^2 θ−m^2 hk sin 2θ)))/((1+m^2 )R cos^2 θ))} for ρ=(((m^2 h cos θ−k sin θ)+(√(k^2 +[(1+m^2 )R^2 −m^2 (h^2 −k^2 )]cos^2 θ−m^2 hk sin 2θ)))/((1+m^2 )cos^2 θ))=R we get θ_1 and θ_2 . Area of shadow=A A=∫_θ_1 ^θ_2 2RϕRdθ ⇒A=2R^2 ∫_θ_1 ^θ_2 cos^(−1) {(((m^2 h cos θ−k sin θ)+(√(k^2 +[(1+m^2 )R^2 −m^2 (h^2 −k^2 )]cos^2 θ−m^2 hk sin 2θ)))/((1+m^2 )R cos^2 θ))}dθ with μ=(k/R),λ=(h/R) ⇒A=2R^2 ∫_θ_1 ^θ_2 cos^(−1) {((m^2 λ cos θ−μ sin θ+(√(μ^2 +[1+m^2 (1+μ^2 −λ^2 )]cos^2 θ−m^2 λμ sin 2θ)))/((1+m^2 )cos^2 θ))}dθ](Q61413.png)
$${eqn}.\:{of}\:{cone}: \\ $$$${x}=\frac{\sqrt{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }}{\mathrm{tan}\:\beta}=\frac{\sqrt{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }}{{m}} \\ $$$${or}\:{y}^{\mathrm{2}} ={m}^{\mathrm{2}} {x}^{\mathrm{2}} −{z}^{\mathrm{2}} \\ $$$$ \\ $$$${eqn}.\:{of}\:{sphere}: \\ $$$$\left({x}−{h}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +\left({z}+{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$ \\ $$$${intersection}\:{of}\:{cone}\:{and}\:{sphere}: \\ $$$$\left({x}−{h}\right)^{\mathrm{2}} +{m}^{\mathrm{2}} {x}^{\mathrm{2}} −{z}^{\mathrm{2}} +\left({z}+{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{1}+{m}^{\mathrm{2}} \right){x}^{\mathrm{2}} −\mathrm{2}{hx}+\mathrm{2}{kz}+\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)=\mathrm{0}\:\:\:...\left({i}\right) \\ $$$$\left({this}\:{is}\:{a}\:{parabola}\:{in}\:{xz}−{plane}\right) \\ $$$$ \\ $$$${at}\:\theta: \\ $$$${let}\:\rho={R}−\Delta{h} \\ $$$${x}={h}−\rho\:\mathrm{cos}\:\theta \\ $$$${z}=−{k}+\rho\:\mathrm{sin}\:\theta \\ $$$${put}\:{this}\:{into}\:\left({i}\right): \\ $$$$\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left[{h}−\rho\:\mathrm{cos}\:\theta\right]^{\mathrm{2}} −\mathrm{2}{h}\left[{h}−\rho\:\mathrm{cos}\:\theta\right]+\mathrm{2}{k}\left[−{k}+\rho\:\mathrm{sin}\:\theta\right]+\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta\:\rho^{\mathrm{2}} −\mathrm{2}\left({m}^{\mathrm{2}} {h}\:\mathrm{cos}\:\theta−{k}\:\mathrm{sin}\:\theta\right)\rho+\left({m}^{\mathrm{2}} {h}^{\mathrm{2}} −{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\rho=\frac{\left({m}^{\mathrm{2}} {h}\:\mathrm{cos}\:\theta−{k}\:\mathrm{sin}\:\theta\right)+\sqrt{{m}^{\mathrm{4}} {h}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta+{k}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta−\mathrm{2}{m}^{\mathrm{2}} {hk}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta−\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta\left({m}^{\mathrm{2}} {h}^{\mathrm{2}} −{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)}}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\left({two}\:{intersections},\:{we}\:{take}\:+\:{for}\:{the}\:{left}\:{one}\right) \\ $$$$\Rightarrow\rho={R}\:\mathrm{cos}\:\varphi=\frac{\left({m}^{\mathrm{2}} {h}\:\mathrm{cos}\:\theta−{k}\:\mathrm{sin}\:\theta\right)+\sqrt{{k}^{\mathrm{2}} +\left[\left(\mathrm{1}+{m}^{\mathrm{2}} \right){R}^{\mathrm{2}} −{m}^{\mathrm{2}} \left({h}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)\right]\mathrm{cos}^{\mathrm{2}} \:\theta−{m}^{\mathrm{2}} {hk}\:\mathrm{sin}\:\mathrm{2}\theta}}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow\varphi=\mathrm{cos}^{−\mathrm{1}} \left\{\frac{\left({m}^{\mathrm{2}} {h}\:\mathrm{cos}\:\theta−{k}\:\mathrm{sin}\:\theta\right)+\sqrt{{k}^{\mathrm{2}} +\left[\left(\mathrm{1}+{m}^{\mathrm{2}} \right){R}^{\mathrm{2}} −{m}^{\mathrm{2}} \left({h}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)\right]\mathrm{cos}^{\mathrm{2}} \:\theta−{m}^{\mathrm{2}} {hk}\:\mathrm{sin}\:\mathrm{2}\theta}}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right){R}\:\mathrm{cos}^{\mathrm{2}} \:\theta}\right\} \\ $$$${for}\:\rho=\frac{\left({m}^{\mathrm{2}} {h}\:\mathrm{cos}\:\theta−{k}\:\mathrm{sin}\:\theta\right)+\sqrt{{k}^{\mathrm{2}} +\left[\left(\mathrm{1}+{m}^{\mathrm{2}} \right){R}^{\mathrm{2}} −{m}^{\mathrm{2}} \left({h}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)\right]\mathrm{cos}^{\mathrm{2}} \:\theta−{m}^{\mathrm{2}} {hk}\:\mathrm{sin}\:\mathrm{2}\theta}}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta}={R} \\ $$$${we}\:{get}\:\theta_{\mathrm{1}} \:{and}\:\theta_{\mathrm{2}} . \\ $$$$ \\ $$$${Area}\:{of}\:{shadow}={A} \\ $$$${A}=\int_{\theta_{\mathrm{1}} } ^{\theta_{\mathrm{2}} } \mathrm{2}{R}\varphi{Rd}\theta \\ $$$$\Rightarrow{A}=\mathrm{2}{R}^{\mathrm{2}} \int_{\theta_{\mathrm{1}} } ^{\theta_{\mathrm{2}} } \mathrm{cos}^{−\mathrm{1}} \left\{\frac{\left({m}^{\mathrm{2}} {h}\:\mathrm{cos}\:\theta−{k}\:\mathrm{sin}\:\theta\right)+\sqrt{{k}^{\mathrm{2}} +\left[\left(\mathrm{1}+{m}^{\mathrm{2}} \right){R}^{\mathrm{2}} −{m}^{\mathrm{2}} \left({h}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)\right]\mathrm{cos}^{\mathrm{2}} \:\theta−{m}^{\mathrm{2}} {hk}\:\mathrm{sin}\:\mathrm{2}\theta}}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right){R}\:\mathrm{cos}^{\mathrm{2}} \:\theta}\right\}{d}\theta \\ $$$${with}\:\mu=\frac{{k}}{{R}},\lambda=\frac{{h}}{{R}} \\ $$$$\Rightarrow{A}=\mathrm{2}{R}^{\mathrm{2}} \int_{\theta_{\mathrm{1}} } ^{\theta_{\mathrm{2}} } \mathrm{cos}^{−\mathrm{1}} \left\{\frac{{m}^{\mathrm{2}} \lambda\:\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta+\sqrt{\mu^{\mathrm{2}} +\left[\mathrm{1}+{m}^{\mathrm{2}} \left(\mathrm{1}+\mu^{\mathrm{2}} −\lambda^{\mathrm{2}} \right)\right]\mathrm{cos}^{\mathrm{2}} \:\theta−{m}^{\mathrm{2}} \lambda\mu\:\mathrm{sin}\:\mathrm{2}\theta}}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta}\right\}{d}\theta \\ $$
Commented by mr W last updated on 02/Jun/19
Commented by mr W last updated on 02/Jun/19
Commented by mr W last updated on 02/Jun/19
Commented by mr W last updated on 02/Jun/19
Commented by ajfour last updated on 02/Jun/19
$${Great}\:{Sir},\:{but}\:{you}'{ll}\:{have}\:{to} \\ $$$${guide}\:{me}\:{to}\:{the}\:{idea}\:{used},\:{i}\:{dont} \\ $$$${think}\:{i}'{ll}\:{follow}\:{it}\:{otherwise}.. \\ $$
Commented by mr W last updated on 02/Jun/19
$${the}\:{boundary}\:{of}\:{the}\:{shadow}\:{on}\:{the} \\ $$$${surface}\:{of}\:{big}\:{sphere}\:{is}\:{the}\:{intersection} \\ $$$$\left({a}\:{curve}\:{in}\:{the}\:{space}\right)\:{from}\:{the}\:{cone} \\ $$$${and}\:{the}\:{big}\:{sphere}.\:{the}\:{shape}\:{of}\:{the} \\ $$$${cone}\:{is}\:{given}\:{by}\:{the}\:{size}\:{of}\:{the}\:{small} \\ $$$${sphere}.\:{with}\:{the}\:{coordinate}\:{system} \\ $$$${i}\:{select}\:{the}\:{eqn}.\:{of}\:{the}\:{cone}\:{and}\:{the} \\ $$$${big}\:{sphere}\:{can}\:{be}\:{described}\:{in}\:{simple} \\ $$$${form}.\:{the}\:{eqn}.\:{of}\:{the}\:{intersection} \\ $$$${line}\:{in}\:{the}\:{xz}−{plane}\:{can}\:{be}\:{obtained} \\ $$$${quite}\:{easily},\:{and}\:{it}'{s}\:{a}\:{parabola}.\:{with} \\ $$$${this}\:{eqn}.\:{we}\:{can}\:{determine}\:{the} \\ $$$${parameters}\:{of}\:{the}\:{shadow}\:{area}\:{on} \\ $$$${the}\:{sphere}\:{surface}.\:{the}\:{parameters} \\ $$$${are}:\:\theta\:{and}\:\rho\:\left({i}.{e}.\:\varphi\right). \\ $$
Commented by ajfour last updated on 06/Jun/19
$${I}\:{am}\:{very}\:{thankful}\:{but}\:{i}\:{lack} \\ $$$${the}\:{required}\:{patience}\:\left({these}\:{days}\right) \\ $$$${Sir},\:{i}\:{have}\:{saved}\:{your}\:{solution}, \\ $$$${and}\:{shall}\:{analyse}\:{it}\:{soon}. \\ $$
Commented by mr W last updated on 06/Jun/19
$${thank}\:{you}\:{sir}! \\ $$$${i}\:{wasn}'{t}\:{able}\:{to}\:{provide}\:{a}\:{better}\:{and} \\ $$$${complete}\:{solution}.\:\:{but}\:{i}'{ll}\:{try}\:{to} \\ $$$${continue}\:{to}\:{think}\:{about}\:{the}\:{question}. \\ $$$${i}\:{hope}\:{one}\:{day}\:{you}\:{may}\:{give}\:{a}\:{perfect} \\ $$$${solution}\:{sir}. \\ $$