Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 61326 by maxmathsup by imad last updated on 01/Jun/19

find ∫_0 ^1 ((sinx)/(1+x^2 ))dx

$${find}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{sinx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$

Commented by perlman last updated on 01/Jun/19

exacte value !

$${exacte}\:{value}\:! \\ $$

Commented by maxmathsup by imad last updated on 01/Jun/19

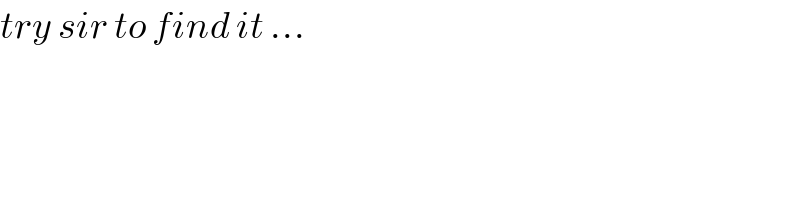
try sir to find it ...

$${try}\:{sir}\:{to}\:{find}\:{it}\:... \\ $$

Commented by abdo mathsup 649 cc last updated on 01/Jun/19

another way we have x−(x^3 /6) ≤sinx ≤x ⇒ (x/(1+x^2 )) −(x^3 /(6(1+x^2 ))) ≤ ((sinx)/(1+x^2 )) ≤ (x/(1+x^2 )) ⇒ ∫_0 ^1 (x/(1+x^2 ))dx −(1/6) ∫_0 ^1 (x^3 /(1+x^2 ))dx ≤ ∫_0 ^1 ((sinx)/(1+x^2 ))dx≤∫_0 ^1 (x/(1+x^2 ))dx ∫_0 ^1 (x/(1+x^2 ))dx =[(1/2)ln(1+x^2 )]_0 ^1 =((ln(2))/2) ∫_0 ^1 (x^3 /(x^2 +1)) dx =∫_0 ^1 ((x(x^2 +1)−x)/(x^2 +1))dx =∫_0 ^1 xdx−∫_0 ^1 ((xdx)/(x^2 +1)) =[(x^2 /2)]_0 ^1 −((ln(2))/2) =(1/2) −((ln(2))/2) ⇒ ((ln(2))/2) −(1/(12)) +((ln(2))/(12)) ≤ ∫_0 ^1 ((sinxdx)/(1+x^2 )) ≤ ((ln(2))/2) ⇒ ((7ln(2)−1)/(12)) ≤ ∫_0 ^1 ((sinx)/(1+x^2 ))dx ≤ ((ln(2))/2) so we can take v_0 =((7ln(2)−1)/(24)) +((ln(2{)/4) =((13ln(2)−1)/(24)) as approximst value for this integral .

$${another}\:{way}\:\:{we}\:{have}\:\:{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\:\leqslant{sinx}\:\leqslant{x}\:\Rightarrow \\ $$$$\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:−\frac{{x}^{\mathrm{3}} }{\mathrm{6}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:\leqslant\:\frac{{sinx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\leqslant\:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:−\frac{\mathrm{1}}{\mathrm{6}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\leqslant\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{sinx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\left[\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)−{x}}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {xdx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{xdx}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{12}}\:+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{12}}\:\leqslant\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{sinxdx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\leqslant\:\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{\mathrm{7}{ln}\left(\mathrm{2}\right)−\mathrm{1}}{\mathrm{12}}\:\leqslant\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{sinx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\leqslant\:\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:\:{so}\:{we}\:{can}\:{take} \\ $$$${v}_{\mathrm{0}} =\frac{\mathrm{7}{ln}\left(\mathrm{2}\right)−\mathrm{1}}{\mathrm{24}}\:+\frac{{ln}\left(\mathrm{2}\left\{\right.\right.}{\mathrm{4}}\:=\frac{\mathrm{13}{ln}\left(\mathrm{2}\right)−\mathrm{1}}{\mathrm{24}}\:{as}\:{approximst} \\ $$$${value}\:{for}\:{this}\:{integral}\:. \\ $$

Commented by abdo mathsup 649 cc last updated on 01/Jun/19

let I =∫_0 ^1 ((sinx)/(1+x^2 )) dx we have sinx =Σ_(n=0) ^∞ (((−1)^n x^(2n+1) )/((2n+1)!)) ⇒ I =∫_0 ^1 (Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!)) x^(2n+1) (1/(1+x^2 )))dx =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!)) ∫_0 ^1 (x^(2n+1) /(1+x^2 ))dx let w_n =∫_0 ^1 (x^(2n+1) /(1+x^2 ))dx ⇒w_n =_(x=tanθ) ∫_0 ^(π/4) ((tan^(2n+1) θ(1+tan^2 θ)dθ)/(1+tan^2 θ)) =∫_0 ^(π/4) tan^(2n+1) θ dθ (the value of this integral is known) ⇒I = Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!)) w_n

$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{sinx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:\:\:{we}\:{have}\:{sinx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:{x}^{\mathrm{2}{n}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:{let}\:{w}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\Rightarrow{w}_{{n}} =_{{x}={tan}\theta} \:\:\:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{tan}^{\mathrm{2}{n}+\mathrm{1}} \theta\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{tan}^{\mathrm{2}{n}+\mathrm{1}} \theta\:{d}\theta\:\:\left({the}\:{value}\:{of}\:{this}\:{integral}\:{is}\right. \\ $$$$\left.{known}\right)\:\Rightarrow{I}\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:{w}_{{n}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com