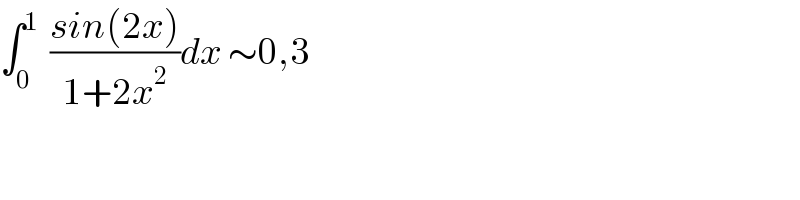Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 61328 by maxmathsup by imad last updated on 01/Jun/19

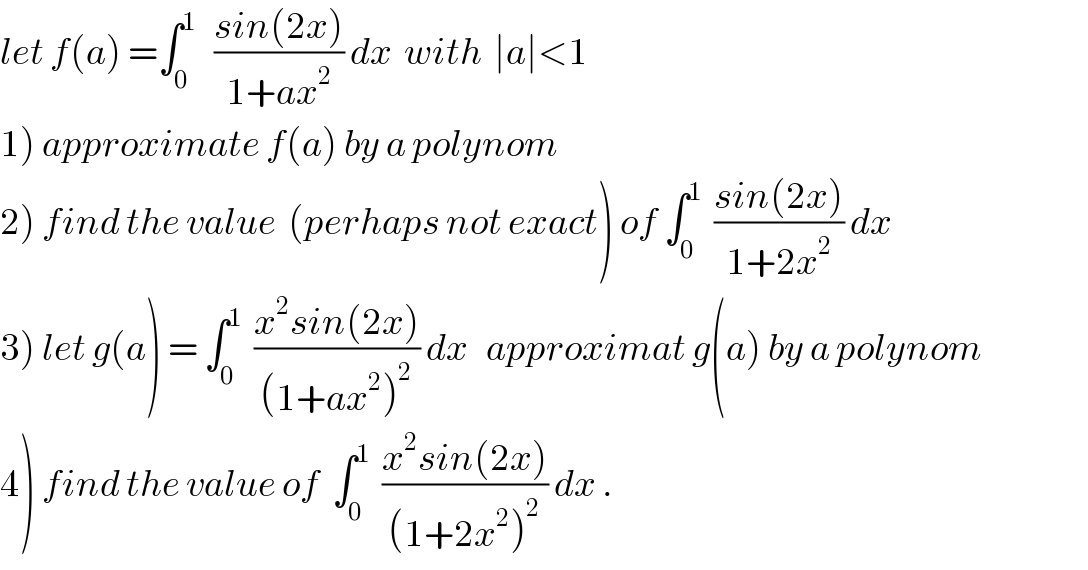
let f(a) =∫_0 ^1 ((sin(2x))/(1+ax^2 )) dx with ∣a∣<1 1) approximate f(a) by a polynom 2) find the value (perhaps not exact) of ∫_0 ^1 ((sin(2x))/(1+2x^2 )) dx 3) let g(a) = ∫_0 ^1 ((x^2 sin(2x))/((1+ax^2 )^2 )) dx approximat g(a) by a polynom 4) find the value of ∫_0 ^1 ((x^2 sin(2x))/((1+2x^2 )^2 )) dx .

$${let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{ax}^{\mathrm{2}} }\:{dx}\:\:{with}\:\:\mid{a}\mid<\mathrm{1} \\ $$ $$\left.\mathrm{1}\right)\:{approximate}\:{f}\left({a}\right)\:{by}\:{a}\:{polynom} \\ $$ $$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:\:\left({perhaps}\:{not}\:{exact}\right)\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }\:{dx} \\ $$ $$\left.\mathrm{3}\right)\:{let}\:{g}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{\mathrm{2}} {sin}\left(\mathrm{2}{x}\right)}{\left(\mathrm{1}+{ax}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:\:\:{approximat}\:{g}\left({a}\right)\:{by}\:{a}\:{polynom} \\ $$ $$\left.\mathrm{4}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{\mathrm{2}} {sin}\left(\mathrm{2}{x}\right)}{\left(\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:. \\ $$

Commented bymaxmathsup by imad last updated on 02/Jun/19

1) the Q is approximate f(a) by a function.

$$\left.\mathrm{1}\right)\:{the}\:{Q}\:{is}\:{approximate}\:{f}\left({a}\right)\:{by}\:{a}\:{function}. \\ $$

Commented bymaxmathsup by imad last updated on 02/Jun/19

1) we have x−(x^3 /6) ≤ sinx ≤ x ⇒2x−((8x^3 )/6) ≤ sin(2x) ≤2x ⇒ 2x−(4/3)x^3 ≤ sin(2x)≤2x ⇒((2x−(4/3)x^3 )/(1+ax^2 )) ≤((sin(2x))/(1+ax^2 )) ≤ ((2x)/(1+ax^2 )) ⇒ ∫_0 ^1 ((2xdx)/(1+ax^2 )) −(4/3) ∫_0 ^1 (x^3 /(1+ax^2 ))dx ≤ ∫_0 ^1 ((sin(2x))/(1+ax^2 )) dx ≤ ∫_0 ^1 ((2x)/(1+ax^2 )) dx ∫_0 ^1 ((2xdx)/(ax^2 +1)) =(1/a) ∫_0 ^1 ((2ax dx)/(ax^2 +1)) =(1/a)[ln(ax^2 +1)]_0 ^1 =((ln(1+a))/a) ( we suppose a≠0 ) ∫_0 ^1 (x^3 /(ax^2 +1)) dx =(1/a) ∫_0 ^1 (((ax^2 +1)x−x)/(ax^2 +1)) dx =(1/a)∫_0 ^1 dx−(1/a) ∫_0 ^1 ((xdx)/(ax^2 +1)) =(1/a) −(1/(2a^2 )) ∫_0 ^1 ((2ax )/(ax^2 +1)) dx =(1/a) −(1/(2a^2 ))[ln(ax^2 +1)]_0 ^1 =(1/a) −((ln(a+1))/(2a^2 )) ⇒ ((ln(1+a))/a) −(4/(3a)) +((2ln(a+1))/(3a^2 )) ≤ f(a) ≤ ((ln(1+a))/a) ⇒ so we can take v_0 =((ln(1+a))/(2a)) −(2/(3a)) +((ln(1+a))/(3a^2 )) +((ln(1+a))/(2a)) =((ln(1+a))/a) −(2/(3a)) +((ln(1+a))/(3a^2 )) ⇒f(a) ∼ ((ln(1+a))/a) −(2/(3a)) +((ln(1+a))/(3a^2 )) with error δ = (1/2){ (4/(3a))−((2ln(a+1))/(3a^2 ))}

$$\left.\mathrm{1}\right)\:\:{we}\:{have}\:\:\:\:{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\:\leqslant\:{sinx}\:\leqslant\:{x}\:\Rightarrow\mathrm{2}{x}−\frac{\mathrm{8}{x}^{\mathrm{3}} }{\mathrm{6}}\:\leqslant\:{sin}\left(\mathrm{2}{x}\right)\:\leqslant\mathrm{2}{x}\:\Rightarrow \\ $$ $$\mathrm{2}{x}−\frac{\mathrm{4}}{\mathrm{3}}{x}^{\mathrm{3}} \:\leqslant\:{sin}\left(\mathrm{2}{x}\right)\leqslant\mathrm{2}{x}\:\Rightarrow\frac{\mathrm{2}{x}−\frac{\mathrm{4}}{\mathrm{3}}{x}^{\mathrm{3}} }{\mathrm{1}+{ax}^{\mathrm{2}} }\:\leqslant\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{ax}^{\mathrm{2}} }\:\leqslant\:\frac{\mathrm{2}{x}}{\mathrm{1}+{ax}^{\mathrm{2}} }\:\Rightarrow \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{xdx}}{\mathrm{1}+{ax}^{\mathrm{2}} }\:−\frac{\mathrm{4}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{\mathrm{3}} }{\mathrm{1}+{ax}^{\mathrm{2}} }{dx}\:\leqslant\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{ax}^{\mathrm{2}} }\:{dx}\:\leqslant\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{x}}{\mathrm{1}+{ax}^{\mathrm{2}} }\:{dx} \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{xdx}}{{ax}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{1}}{{a}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{ax}\:{dx}}{{ax}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{1}}{{a}}\left[{ln}\left({ax}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{{ln}\left(\mathrm{1}+{a}\right)}{{a}}\:\:\:\left(\:{we}\:{suppose}\:{a}\neq\mathrm{0}\:\right) \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{\mathrm{3}} }{{ax}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:=\frac{\mathrm{1}}{{a}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left({ax}^{\mathrm{2}} +\mathrm{1}\right){x}−{x}}{{ax}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:\:=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \:{dx}−\frac{\mathrm{1}}{{a}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{xdx}}{{ax}^{\mathrm{2}} \:+\mathrm{1}} \\ $$ $$=\frac{\mathrm{1}}{{a}}\:−\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{ax}\:}{{ax}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:=\frac{\mathrm{1}}{{a}}\:−\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} }\left[{ln}\left({ax}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{1}}{{a}}\:−\frac{{ln}\left({a}+\mathrm{1}\right)}{\mathrm{2}{a}^{\mathrm{2}} }\:\Rightarrow \\ $$ $$\frac{{ln}\left(\mathrm{1}+{a}\right)}{{a}}\:−\frac{\mathrm{4}}{\mathrm{3}{a}}\:+\frac{\mathrm{2}{ln}\left({a}+\mathrm{1}\right)}{\mathrm{3}{a}^{\mathrm{2}} }\:\leqslant\:{f}\left({a}\right)\:\leqslant\:\frac{{ln}\left(\mathrm{1}+{a}\right)}{{a}}\:\Rightarrow \\ $$ $${so}\:{we}\:{can}\:{take}\:\:{v}_{\mathrm{0}} =\frac{{ln}\left(\mathrm{1}+{a}\right)}{\mathrm{2}{a}}\:−\frac{\mathrm{2}}{\mathrm{3}{a}}\:+\frac{{ln}\left(\mathrm{1}+{a}\right)}{\mathrm{3}{a}^{\mathrm{2}} }\:+\frac{{ln}\left(\mathrm{1}+{a}\right)}{\mathrm{2}{a}} \\ $$ $$=\frac{{ln}\left(\mathrm{1}+{a}\right)}{{a}}\:−\frac{\mathrm{2}}{\mathrm{3}{a}}\:+\frac{{ln}\left(\mathrm{1}+{a}\right)}{\mathrm{3}{a}^{\mathrm{2}} }\:\Rightarrow{f}\left({a}\right)\:\sim\:\frac{{ln}\left(\mathrm{1}+{a}\right)}{{a}}\:−\frac{\mathrm{2}}{\mathrm{3}{a}}\:+\frac{{ln}\left(\mathrm{1}+{a}\right)}{\mathrm{3}{a}^{\mathrm{2}} } \\ $$ $${with}\:{error}\:\delta\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{\mathrm{4}}{\mathrm{3}{a}}−\frac{\mathrm{2}{ln}\left({a}+\mathrm{1}\right)}{\mathrm{3}{a}^{\mathrm{2}} }\right\} \\ $$ $$ \\ $$

Commented bymaxmathsup by imad last updated on 02/Jun/19

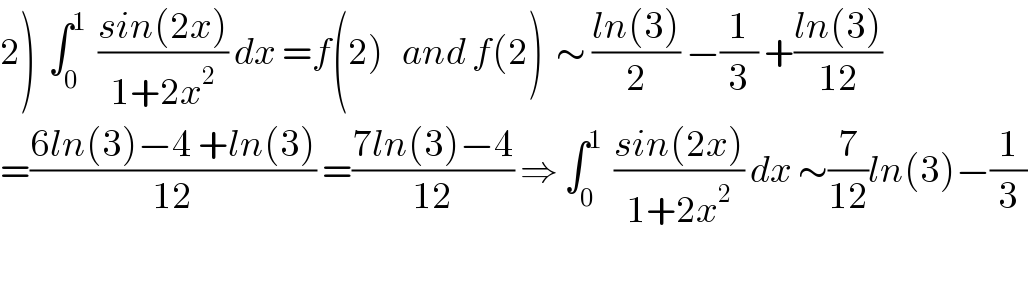
2) ∫_0 ^1 ((sin(2x))/(1+2x^2 )) dx =f(2) and f(2) ∼ ((ln(3))/2) −(1/3) +((ln(3))/(12)) =((6ln(3)−4 +ln(3))/(12)) =((7ln(3)−4)/(12)) ⇒ ∫_0 ^1 ((sin(2x))/(1+2x^2 )) dx ∼(7/(12))ln(3)−(1/3)

$$\left.\mathrm{2}\right)\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }\:{dx}\:={f}\left(\mathrm{2}\right)\:\:\:{and}\:{f}\left(\mathrm{2}\right)\:\:\sim\:\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{12}} \\ $$ $$=\frac{\mathrm{6}{ln}\left(\mathrm{3}\right)−\mathrm{4}\:+{ln}\left(\mathrm{3}\right)}{\mathrm{12}}\:=\frac{\mathrm{7}{ln}\left(\mathrm{3}\right)−\mathrm{4}}{\mathrm{12}}\:\Rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }\:{dx}\:\sim\frac{\mathrm{7}}{\mathrm{12}}{ln}\left(\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{3}} \\ $$ $$ \\ $$

Commented bymaxmathsup by imad last updated on 02/Jun/19

∫_0 ^1 ((sin(2x))/(1+2x^2 ))dx ∼0,3

$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }{dx}\:\sim\mathrm{0},\mathrm{3} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com