Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 61386 by maxmathsup by imad last updated on 02/Jun/19

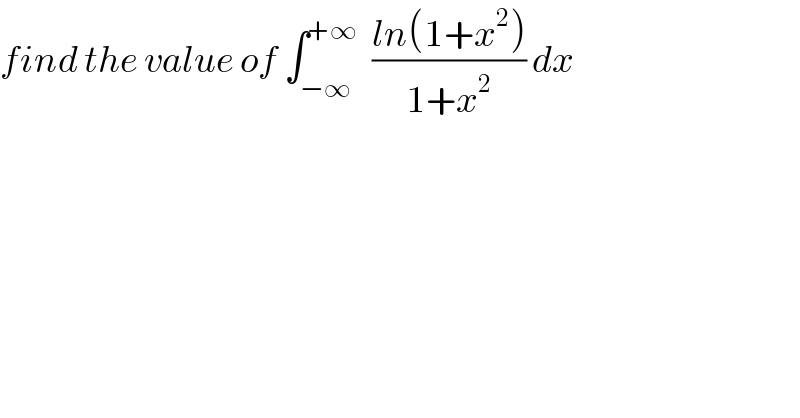
find the value of ∫_(−∞) ^(+∞) ((ln(1+x^2 ))/(1+x^2 )) dx

$${find}\:{the}\:{value}\:{of}\:\int_{−\infty} ^{+\infty} \:\:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx} \\ $$

Commented by perlman last updated on 02/Jun/19

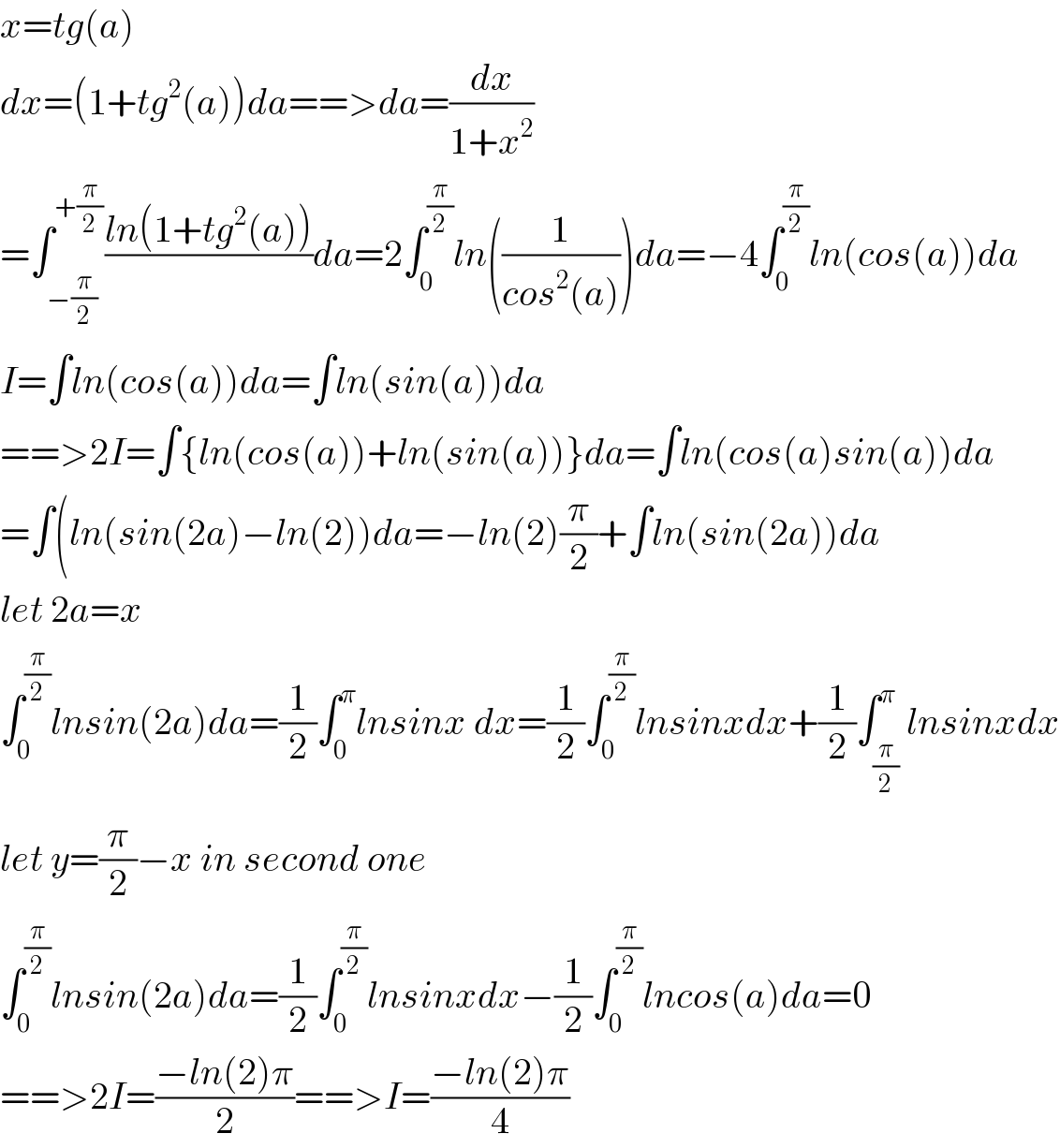
x=tg(a) dx=(1+tg^2 (a))da==>da=(dx/(1+x^2 )) =∫_(−(π/2)) ^(+(π/2)) ((ln(1+tg^2 (a)))/)da=2∫_0 ^(π/2) ln((1/(cos^2 (a))))da=−4∫_0 ^(π/2) ln(cos(a))da I=∫ln(cos(a))da=∫ln(sin(a))da ==>2I=∫{ln(cos(a))+ln(sin(a))}da=∫ln(cos(a)sin(a))da =∫(ln(sin(2a)−ln(2))da=−ln(2)(π/2)+∫ln(sin(2a))da let 2a=x ∫_0 ^(π/2) lnsin(2a)da=(1/2)∫_0 ^π lnsinx dx=(1/2)∫_0 ^(π/2) lnsinxdx+(1/2)∫_(π/2) ^π lnsinxdx let y=(π/2)−x in second one ∫_0 ^(π/2) lnsin(2a)da=(1/2)∫_0 ^(π/2) lnsinxdx−(1/2)∫_0 ^(π/2) lncos(a)da=0 ==>2I=((−ln(2)π)/2)==>I=((−ln(2)π)/4)

$${x}={tg}\left({a}\right) \\ $$$${dx}=\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({a}\right)\right){da}==>{da}=\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$=\int_{−\frac{\pi}{\mathrm{2}}} ^{+\frac{\pi}{\mathrm{2}}} \frac{{ln}\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({a}\right)\right)}{}{da}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({a}\right)}\right){da}=−\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\left({a}\right)\right){da} \\ $$$${I}=\int{ln}\left({cos}\left({a}\right)\right){da}=\int{ln}\left({sin}\left({a}\right)\right){da} \\ $$$$==>\mathrm{2}{I}=\int\left\{{ln}\left({cos}\left({a}\right)\right)+{ln}\left({sin}\left({a}\right)\right)\right\}{da}=\int{ln}\left({cos}\left({a}\right){sin}\left({a}\right)\right){da} \\ $$$$=\int\left({ln}\left({sin}\left(\mathrm{2}{a}\right)−{ln}\left(\mathrm{2}\right)\right){da}=−{ln}\left(\mathrm{2}\right)\frac{\pi}{\mathrm{2}}+\int{ln}\left({sin}\left(\mathrm{2}{a}\right)\right){da}\right. \\ $$$${let}\:\mathrm{2}{a}={x} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {lnsin}\left(\mathrm{2}{a}\right){da}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} {lnsinx}\:{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {lnsinxdx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} {lnsinxdx} \\ $$$${let}\:{y}=\frac{\pi}{\mathrm{2}}−{x}\:{in}\:{second}\:{one} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {lnsin}\left(\mathrm{2}{a}\right){da}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {lnsinxdx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {lncos}\left({a}\right){da}=\mathrm{0} \\ $$$$==>\mathrm{2}{I}=\frac{−{ln}\left(\mathrm{2}\right)\pi}{\mathrm{2}}==>{I}=\frac{−{ln}\left(\mathrm{2}\right)\pi}{\mathrm{4}} \\ $$

Commented by maxmathsup by imad last updated on 02/Jun/19

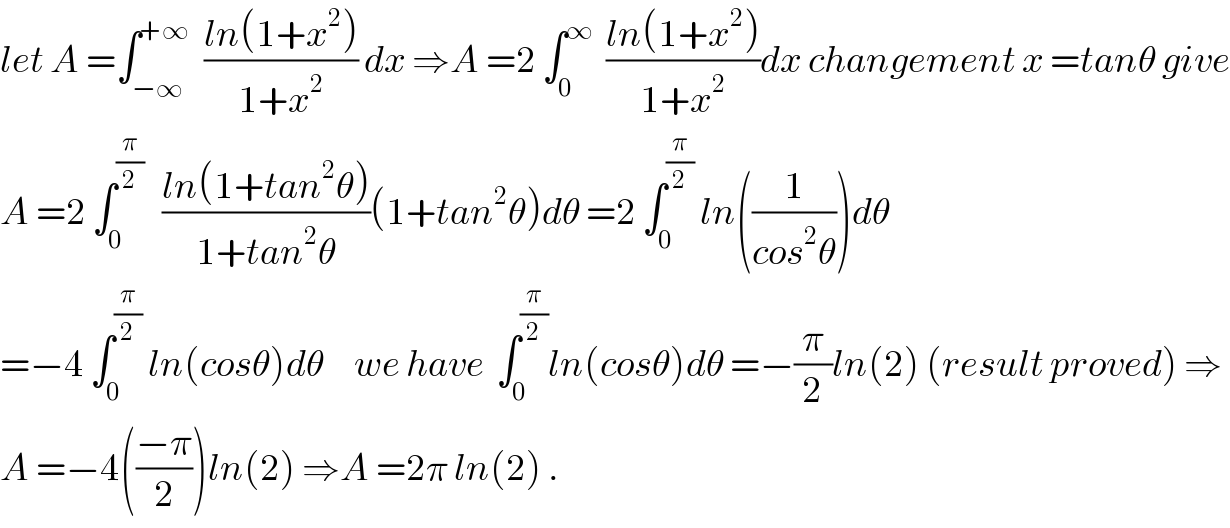
let A =∫_(−∞) ^(+∞) ((ln(1+x^2 ))/(1+x^2 )) dx ⇒A =2 ∫_0 ^∞ ((ln(1+x^2 ))/(1+x^2 ))dx changement x =tanθ give A =2 ∫_0 ^(π/2) ((ln(1+tan^2 θ))/(1+tan^2 θ))(1+tan^2 θ)dθ =2 ∫_0 ^(π/2) ln((1/(cos^2 θ)))dθ =−4 ∫_0 ^(π/2) ln(cosθ)dθ we have ∫_0 ^(π/2) ln(cosθ)dθ =−(π/2)ln(2) (result proved) ⇒ A =−4(((−π)/2))ln(2) ⇒A =2π ln(2) .

$${let}\:{A}\:=\int_{−\infty} ^{+\infty} \:\:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:\Rightarrow{A}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:{changement}\:{x}\:={tan}\theta\:{give} \\ $$$${A}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \theta}\right){d}\theta \\ $$$$=−\mathrm{4}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left({cos}\theta\right){d}\theta\:\:\:\:\:{we}\:{have}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\theta\right){d}\theta\:=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:\left({result}\:{proved}\right)\:\Rightarrow \\ $$$${A}\:=−\mathrm{4}\left(\frac{−\pi}{\mathrm{2}}\right){ln}\left(\mathrm{2}\right)\:\Rightarrow{A}\:=\mathrm{2}\pi\:{ln}\left(\mathrm{2}\right)\:. \\ $$

Commented by maxmathsup by imad last updated on 02/Jun/19

parametric way let f(t) =∫_(−∞) ^(+∞) ((ln(1+tx^2 ))/(1+x^2 )) dx with t≥0 f^′ (t) =∫_(−∞) ^(+∞) (x^2 /((1+tx^2 )(x^2 +1))) dx let ϕ(z) =(z^2 /((tz^2 +1)(z^2 +1))) poles of ϕ? ϕ(z) =(z^2 /(((√t)z−i)((√t)z +i)(z−i)(z+i))) =(z^2 /(t(z−(i/(√t)))(z+(i/(√t)))(z−i)(z+i))) the poles of ϕ are +^− i and +^− (i/(√t)) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,i) +Res(ϕ,(i/(√t)))} Res(ϕ,i) =lim_(z→i) (z−i)ϕ(z) = ((−1)/((1−t)2i)) =((−1)/(2i(1−t))) Res(ϕ,(i/(√t))) =lim_(z→(i/(√t))) (z−(i/(√t)))ϕ(z) =((−1)/(t^2 (((2i)/(√t)))(−(1/t)+1))) =((−t(√t))/(2it^2 (t−1))) =−((√t)/(2it(t−1))) ⇒∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ ((−1)/(2i(1−t))) +((√t)/(2it(1−t)))} =π{((√t)/(t(1−t))) −(1/(1−t))} =f^′ (t) ⇒ f(t) =π ∫ (((√t)dt)/(t(1−t))) −π ∫ (dt/(1−t)) +c ∫ (dt/(1−t)) =−ln∣1−t∣ +c_0 ∫ (((√t)dt)/(t(1−t))) =_((√t)=u) ∫ ((u(2u)du)/(u^2 (1−u^2 ))) = ∫ ((2du)/(1−u^2 )) =∫ {(1/(1−u)) +(1/(1+u))}du =ln∣((1+u)/(1−u))∣ +c_1 =ln∣((1+(√t))/(1−(√t)))∣ +c_1 ⇒ f(t) =πln∣((1+(√t))/(1−(√t)))∣ +πln∣1−t∣ +c f(0) =0 =c ⇒f(t) =πln∣((1+(√t))/(1−(√t)))∣ +πln∣1−t∣ . ∫_(−∞) ^(+∞) ((ln(1+x^2 ))/(1+x^2 )) dx =lim_(x→1) f(1) let find this limit f(t) =πln∣1+(√t)∣−πln∣1−(√t)∣+πln∣1−t∣ ⇒ f(u^2 ) =πln(1+u)−πln∣1−u∣ +πln∣1−u^2 ∣ =2πln(1+u) ⇒ lim_(t→1) f(t) =lim_(u→1) f(u^2 ) =2πln(2) ⇒★∫_(−∞) ^(+∞) ((ln(1+x^2 ))/(1+x^2 )) dx =2πln(2)★ and generally ∫_(−∞) ^(+∞) ((ln(1+tx^2 ))/(1+x^2 ))dx =πln∣((1+(√t))/(1−(√t)))∣ +πln∣1−t∣ with t≥0

$${parametric}\:\:{way}\:\:\:\:{let}\:{f}\left({t}\right)\:=\int_{−\infty} ^{+\infty} \:\frac{{ln}\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:{with}\:{t}\geqslant\mathrm{0} \\ $$$${f}^{'} \left({t}\right)\:=\int_{−\infty} ^{+\infty} \:\:\:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:{dx}\:\:\:{let}\:\varphi\left({z}\right)\:=\frac{{z}^{\mathrm{2}} }{\left({tz}^{\mathrm{2}} +\mathrm{1}\right)\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\:\:{poles}\:{of}\:\varphi? \\ $$$$\varphi\left({z}\right)\:=\frac{{z}^{\mathrm{2}} }{\left(\sqrt{{t}}{z}−{i}\right)\left(\sqrt{{t}}{z}\:+{i}\right)\left({z}−{i}\right)\left({z}+{i}\right)}\:=\frac{{z}^{\mathrm{2}} }{{t}\left({z}−\frac{{i}}{\sqrt{{t}}}\right)\left({z}+\frac{{i}}{\sqrt{{t}}}\right)\left({z}−{i}\right)\left({z}+{i}\right)} \\ $$$${the}\:{poles}\:{of}\:\varphi\:{are}\:\overset{−} {+}{i}\:\:{and}\:\overset{−} {+}\frac{{i}}{\sqrt{{t}}}\:\:{residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{i}\right)\:+{Res}\left(\varphi,\frac{{i}}{\sqrt{{t}}}\right)\right\} \\ $$$${Res}\left(\varphi,{i}\right)\:={lim}_{{z}\rightarrow{i}} \left({z}−{i}\right)\varphi\left({z}\right)\:=\:\frac{−\mathrm{1}}{\left(\mathrm{1}−{t}\right)\mathrm{2}{i}}\:=\frac{−\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{1}−{t}\right)} \\ $$$${Res}\left(\varphi,\frac{{i}}{\sqrt{{t}}}\right)\:={lim}_{{z}\rightarrow\frac{{i}}{\sqrt{{t}}}} \:\:\:\left({z}−\frac{{i}}{\sqrt{{t}}}\right)\varphi\left({z}\right)\:=\frac{−\mathrm{1}}{{t}^{\mathrm{2}} \left(\frac{\mathrm{2}{i}}{\sqrt{{t}}}\right)\left(−\frac{\mathrm{1}}{{t}}+\mathrm{1}\right)}\:=\frac{−{t}\sqrt{{t}}}{\mathrm{2}{it}^{\mathrm{2}} \left({t}−\mathrm{1}\right)}\:=−\frac{\sqrt{{t}}}{\mathrm{2}{it}\left({t}−\mathrm{1}\right)} \\ $$$$\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\frac{−\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{1}−{t}\right)}\:+\frac{\sqrt{{t}}}{\mathrm{2}{it}\left(\mathrm{1}−{t}\right)}\right\}\:=\pi\left\{\frac{\sqrt{{t}}}{{t}\left(\mathrm{1}−{t}\right)}\:−\frac{\mathrm{1}}{\mathrm{1}−{t}}\right\}\:={f}^{'} \left({t}\right)\:\Rightarrow \\ $$$${f}\left({t}\right)\:=\pi\:\int\:\:\frac{\sqrt{{t}}{dt}}{{t}\left(\mathrm{1}−{t}\right)}\:−\pi\:\int\:\frac{{dt}}{\mathrm{1}−{t}}\:+{c} \\ $$$$\int\:\:\frac{{dt}}{\mathrm{1}−{t}}\:=−{ln}\mid\mathrm{1}−{t}\mid\:+{c}_{\mathrm{0}} \\ $$$$\int\:\:\frac{\sqrt{{t}}{dt}}{{t}\left(\mathrm{1}−{t}\right)}\:=_{\sqrt{{t}}={u}} \:\:\:\:\:\:\int\:\frac{{u}\left(\mathrm{2}{u}\right){du}}{{u}^{\mathrm{2}} \left(\mathrm{1}−{u}^{\mathrm{2}} \right)}\:=\:\int\:\:\frac{\mathrm{2}{du}}{\mathrm{1}−{u}^{\mathrm{2}} }\:=\int\:\:\left\{\frac{\mathrm{1}}{\mathrm{1}−{u}}\:+\frac{\mathrm{1}}{\mathrm{1}+{u}}\right\}{du} \\ $$$$={ln}\mid\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid\:+{c}_{\mathrm{1}} ={ln}\mid\frac{\mathrm{1}+\sqrt{{t}}}{\mathrm{1}−\sqrt{{t}}}\mid\:+{c}_{\mathrm{1}} \:\Rightarrow \\ $$$${f}\left({t}\right)\:=\pi{ln}\mid\frac{\mathrm{1}+\sqrt{{t}}}{\mathrm{1}−\sqrt{{t}}}\mid\:+\pi{ln}\mid\mathrm{1}−{t}\mid\:+{c} \\ $$$${f}\left(\mathrm{0}\right)\:=\mathrm{0}\:={c}\:\Rightarrow{f}\left({t}\right)\:=\pi{ln}\mid\frac{\mathrm{1}+\sqrt{{t}}}{\mathrm{1}−\sqrt{{t}}}\mid\:+\pi{ln}\mid\mathrm{1}−{t}\mid\:. \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:={lim}_{{x}\rightarrow\mathrm{1}} {f}\left(\mathrm{1}\right)\:\:\:{let}\:{find}\:\:{this}\:{limit} \\ $$$${f}\left({t}\right)\:=\pi{ln}\mid\mathrm{1}+\sqrt{{t}}\mid−\pi{ln}\mid\mathrm{1}−\sqrt{{t}}\mid+\pi{ln}\mid\mathrm{1}−{t}\mid\:\Rightarrow \\ $$$${f}\left({u}^{\mathrm{2}} \right)\:=\pi{ln}\left(\mathrm{1}+{u}\right)−\pi{ln}\mid\mathrm{1}−{u}\mid\:+\pi{ln}\mid\mathrm{1}−{u}^{\mathrm{2}} \mid\:=\mathrm{2}\pi{ln}\left(\mathrm{1}+{u}\right)\:\Rightarrow \\ $$$${lim}_{{t}\rightarrow\mathrm{1}} {f}\left({t}\right)\:={lim}_{{u}\rightarrow\mathrm{1}} {f}\left({u}^{\mathrm{2}} \right)\:=\mathrm{2}\pi{ln}\left(\mathrm{2}\right)\:\:\:\Rightarrow\bigstar\int_{−\infty} ^{+\infty} \:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:=\mathrm{2}\pi{ln}\left(\mathrm{2}\right)\bigstar \\ $$$${and}\:{generally}\:\:\:\int_{−\infty} ^{+\infty} \:\frac{{ln}\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\pi{ln}\mid\frac{\mathrm{1}+\sqrt{{t}}}{\mathrm{1}−\sqrt{{t}}}\mid\:+\pi{ln}\mid\mathrm{1}−{t}\mid\:\:\:{with}\:{t}\geqslant\mathrm{0} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com