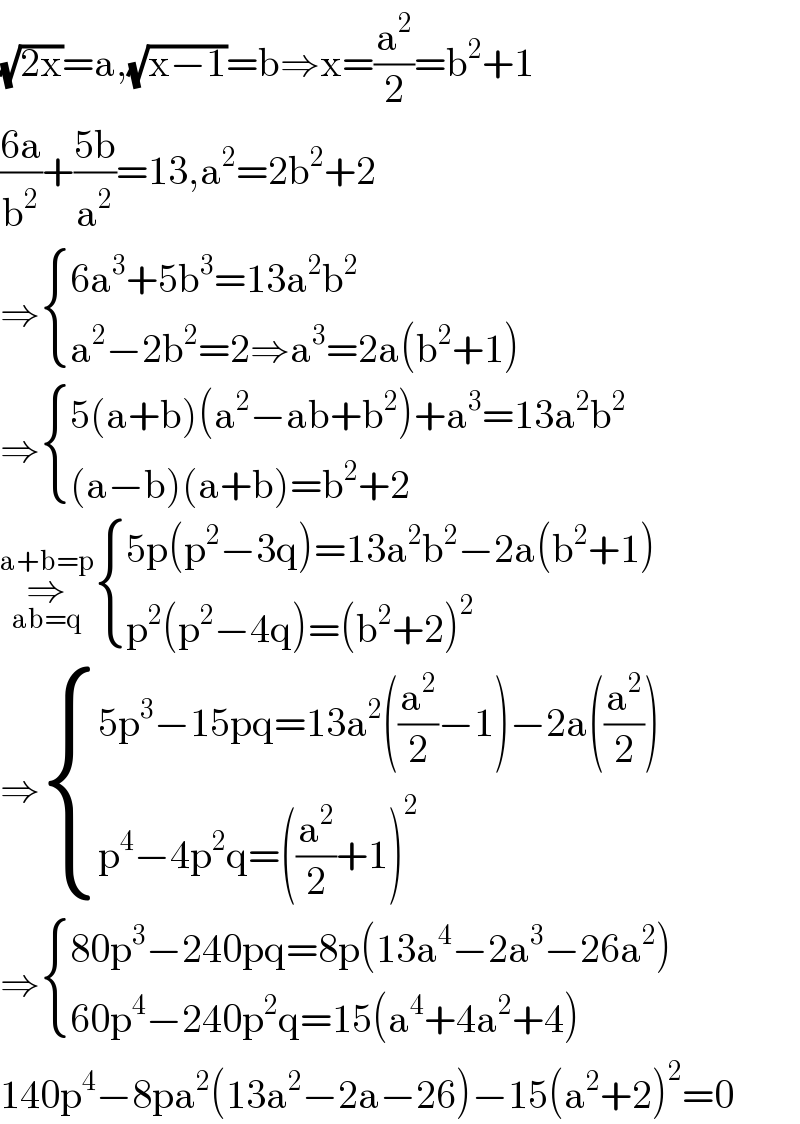Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 61479 by Tawa1 last updated on 03/Jun/19

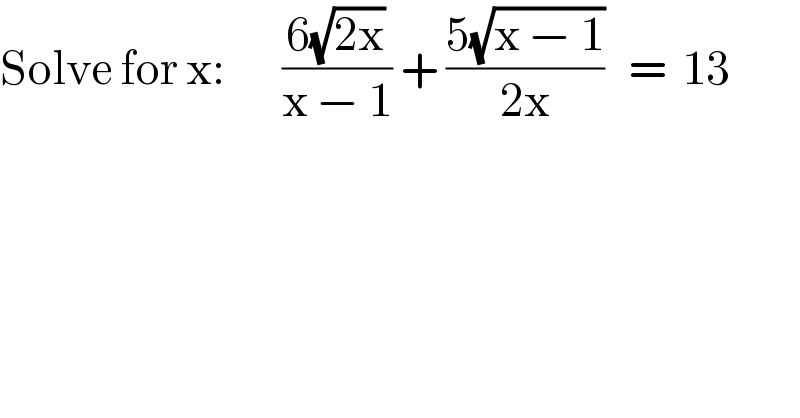
Solve for x: ((6(√(2x)))/(x − 1)) + ((5(√(x − 1)))/(2x)) = 13

$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x}:\:\:\:\:\:\:\:\frac{\mathrm{6}\sqrt{\mathrm{2x}}}{\mathrm{x}\:−\:\mathrm{1}}\:+\:\frac{\mathrm{5}\sqrt{\mathrm{x}\:−\:\mathrm{1}}}{\mathrm{2x}}\:\:\:=\:\:\mathrm{13} \\ $$

Commented by MJS last updated on 03/Jun/19

we cannot generally solve this...

$$\mathrm{we}\:\mathrm{cannot}\:\mathrm{generally}\:\mathrm{solve}\:\mathrm{this}... \\ $$

Answered by ajfour last updated on 03/Jun/19

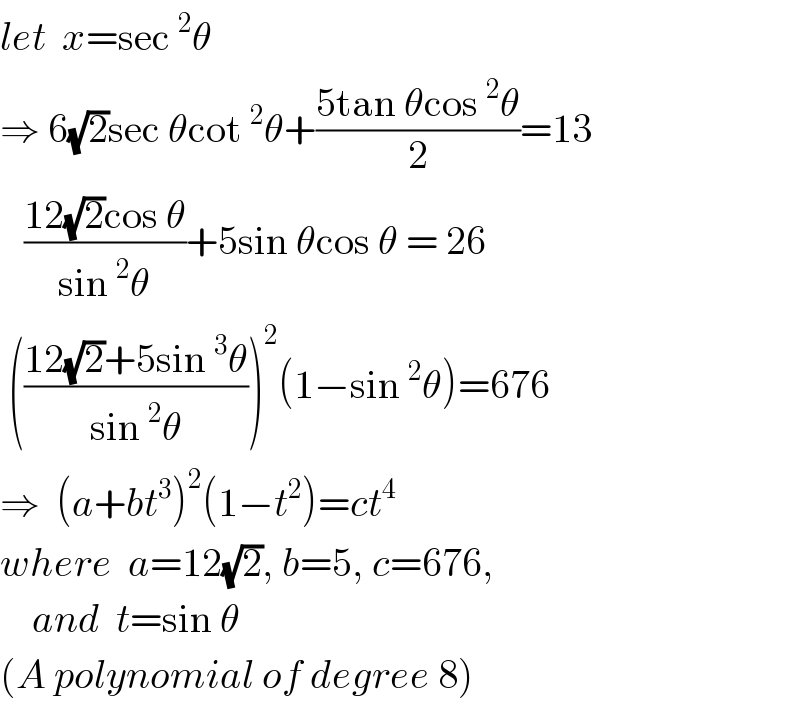
let x=sec^2 θ ⇒ 6(√2)sec θcot^2 θ+((5tan θcos^2 θ)/2)=13 ((12(√2)cos θ)/(sin^2 θ))+5sin θcos θ = 26 (((12(√2)+5sin^3 θ)/(sin^2 θ)))^2 (1−sin^2 θ)=676 ⇒ (a+bt^3 )^2 (1−t^2 )=ct^4 where a=12(√2), b=5, c=676, and t=sin θ (A polynomial of degree 8)

$${let}\:\:{x}=\mathrm{sec}\:^{\mathrm{2}} \theta \\ $$$$\Rightarrow\:\mathrm{6}\sqrt{\mathrm{2}}\mathrm{sec}\:\theta\mathrm{cot}\:^{\mathrm{2}} \theta+\frac{\mathrm{5tan}\:\theta\mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{2}}=\mathrm{13} \\ $$$$\:\:\:\frac{\mathrm{12}\sqrt{\mathrm{2}}\mathrm{cos}\:\theta}{\mathrm{sin}\:^{\mathrm{2}} \theta}+\mathrm{5sin}\:\theta\mathrm{cos}\:\theta\:=\:\mathrm{26} \\ $$$$\:\left(\frac{\mathrm{12}\sqrt{\mathrm{2}}+\mathrm{5sin}\:^{\mathrm{3}} \theta}{\mathrm{sin}\:^{\mathrm{2}} \theta}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \theta\right)=\mathrm{676} \\ $$$$\Rightarrow\:\:\left({a}+{bt}^{\mathrm{3}} \right)^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)={ct}^{\mathrm{4}} \\ $$$${where}\:\:{a}=\mathrm{12}\sqrt{\mathrm{2}},\:{b}=\mathrm{5},\:{c}=\mathrm{676}, \\ $$$$\:\:\:\:{and}\:\:{t}=\mathrm{sin}\:\theta \\ $$$$\left({A}\:{polynomial}\:{of}\:{degree}\:\mathrm{8}\right) \\ $$

Commented by Tawa1 last updated on 03/Jun/19

Ohh.

$$\mathrm{Ohh}.\:\: \\ $$

Answered by MJS last updated on 03/Jun/19

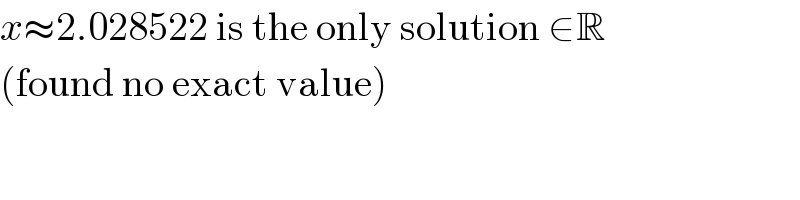
x≈2.028522 is the only solution ∈R (found no exact value)

$${x}\approx\mathrm{2}.\mathrm{028522}\:\mathrm{is}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution}\:\in\mathbb{R} \\ $$$$\left(\mathrm{found}\:\mathrm{no}\:\mathrm{exact}\:\mathrm{value}\right) \\ $$

Commented by Tawa1 last updated on 03/Jun/19

Any workings sir

$$\mathrm{Any}\:\mathrm{workings}\:\mathrm{sir} \\ $$

Commented by MJS last updated on 03/Jun/19

we can square it 2 times but we end up with a polynome of degree 8 which has got no trivial solution [squaring like this: (√a)+(√b)=c a+(√a)(√b)+b=c^2 ab=(c^2 −a−b)^2 ] approximated using a calculator the equation is defined for x>1 so I started with x=1.5, x=2, x=2.5

$$\mathrm{we}\:\mathrm{can}\:\mathrm{square}\:\mathrm{it}\:\mathrm{2}\:\mathrm{times}\:\mathrm{but}\:\mathrm{we}\:\mathrm{end}\:\mathrm{up}\:\mathrm{with} \\ $$$$\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{degree}\:\mathrm{8}\:\mathrm{which}\:\mathrm{has}\:\mathrm{got}\:\mathrm{no} \\ $$$$\mathrm{trivial}\:\mathrm{solution} \\ $$$$\left[\mathrm{squaring}\:\mathrm{like}\:\mathrm{this}:\right. \\ $$$$\sqrt{{a}}+\sqrt{{b}}={c} \\ $$$${a}+\sqrt{{a}}\sqrt{{b}}+{b}={c}^{\mathrm{2}} \\ $$$$\left.{ab}=\left({c}^{\mathrm{2}} −{a}−{b}\right)^{\mathrm{2}} \right] \\ $$$$ \\ $$$$\mathrm{approximated}\:\mathrm{using}\:\mathrm{a}\:\mathrm{calculator} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:{x}>\mathrm{1}\:\mathrm{so}\:\mathrm{I}\:\mathrm{started} \\ $$$$\mathrm{with}\:{x}=\mathrm{1}.\mathrm{5},\:{x}=\mathrm{2},\:{x}=\mathrm{2}.\mathrm{5} \\ $$

Answered by behi83417@gmail.com last updated on 03/Jun/19

(√(2x))=a,(√(x−1))=b⇒x=(a^2 /2)=b^2 +1 ((6a)/b^2 )+((5b)/a^2 )=13,a^2 =2b^2 +2 ⇒ { ((6a^3 +5b^3 =13a^2 b^2 )),((a^2 −2b^2 =2⇒a^3 =2a(b^2 +1))) :} ⇒ { ((5(a+b)(a^2 −ab+b^2 )+a^3 =13a^2 b^2 )),(((a−b)(a+b)=b^2 +2)) :} ⇒_(ab=q) ^(a+b=p) { ((5p(p^2 −3q)=13a^2 b^2 −2a(b^2 +1))),((p^2 (p^2 −4q)=(b^2 +2)^2 )) :} ⇒ { ((5p^3 −15pq=13a^2 ((a^2 /2)−1)−2a((a^2 /2)))),((p^4 −4p^2 q=((a^2 /2)+1)^2 )) :} ⇒ { ((80p^3 −240pq=8p(13a^4 −2a^3 −26a^2 ))),((60p^4 −240p^2 q=15(a^4 +4a^2 +4))) :} 140p^4 −8pa^2 (13a^2 −2a−26)−15(a^2 +2)^2 =0

$$\sqrt{\mathrm{2x}}=\mathrm{a},\sqrt{\mathrm{x}−\mathrm{1}}=\mathrm{b}\Rightarrow\mathrm{x}=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{b}^{\mathrm{2}} +\mathrm{1} \\ $$$$\frac{\mathrm{6a}}{\mathrm{b}^{\mathrm{2}} }+\frac{\mathrm{5b}}{\mathrm{a}^{\mathrm{2}} }=\mathrm{13},\mathrm{a}^{\mathrm{2}} =\mathrm{2b}^{\mathrm{2}} +\mathrm{2} \\ $$$$\Rightarrow\begin{cases}{\mathrm{6a}^{\mathrm{3}} +\mathrm{5b}^{\mathrm{3}} =\mathrm{13a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} }\\{\mathrm{a}^{\mathrm{2}} −\mathrm{2b}^{\mathrm{2}} =\mathrm{2}\Rightarrow\mathrm{a}^{\mathrm{3}} =\mathrm{2a}\left(\mathrm{b}^{\mathrm{2}} +\mathrm{1}\right)}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{5}\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{a}^{\mathrm{2}} −\mathrm{ab}+\mathrm{b}^{\mathrm{2}} \right)+\mathrm{a}^{\mathrm{3}} =\mathrm{13a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} }\\{\left(\mathrm{a}−\mathrm{b}\right)\left(\mathrm{a}+\mathrm{b}\right)=\mathrm{b}^{\mathrm{2}} +\mathrm{2}}\end{cases} \\ $$$$\underset{\mathrm{ab}=\mathrm{q}} {\overset{\mathrm{a}+\mathrm{b}=\mathrm{p}} {\Rightarrow}}\begin{cases}{\mathrm{5p}\left(\mathrm{p}^{\mathrm{2}} −\mathrm{3q}\right)=\mathrm{13a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} −\mathrm{2a}\left(\mathrm{b}^{\mathrm{2}} +\mathrm{1}\right)}\\{\mathrm{p}^{\mathrm{2}} \left(\mathrm{p}^{\mathrm{2}} −\mathrm{4q}\right)=\left(\mathrm{b}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{5p}^{\mathrm{3}} −\mathrm{15pq}=\mathrm{13a}^{\mathrm{2}} \left(\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}\right)−\mathrm{2a}\left(\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}\right)}\\{\mathrm{p}^{\mathrm{4}} −\mathrm{4p}^{\mathrm{2}} \mathrm{q}=\left(\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} }\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{80p}^{\mathrm{3}} −\mathrm{240pq}=\mathrm{8p}\left(\mathrm{13a}^{\mathrm{4}} −\mathrm{2a}^{\mathrm{3}} −\mathrm{26a}^{\mathrm{2}} \right)}\\{\mathrm{60p}^{\mathrm{4}} −\mathrm{240p}^{\mathrm{2}} \mathrm{q}=\mathrm{15}\left(\mathrm{a}^{\mathrm{4}} +\mathrm{4a}^{\mathrm{2}} +\mathrm{4}\right)}\end{cases} \\ $$$$\mathrm{140p}^{\mathrm{4}} −\mathrm{8pa}^{\mathrm{2}} \left(\mathrm{13a}^{\mathrm{2}} −\mathrm{2a}−\mathrm{26}\right)−\mathrm{15}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} =\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com