Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 6157 by Rasheed Soomro last updated on 16/Jun/16

Answered by Yozzii last updated on 16/Jun/16

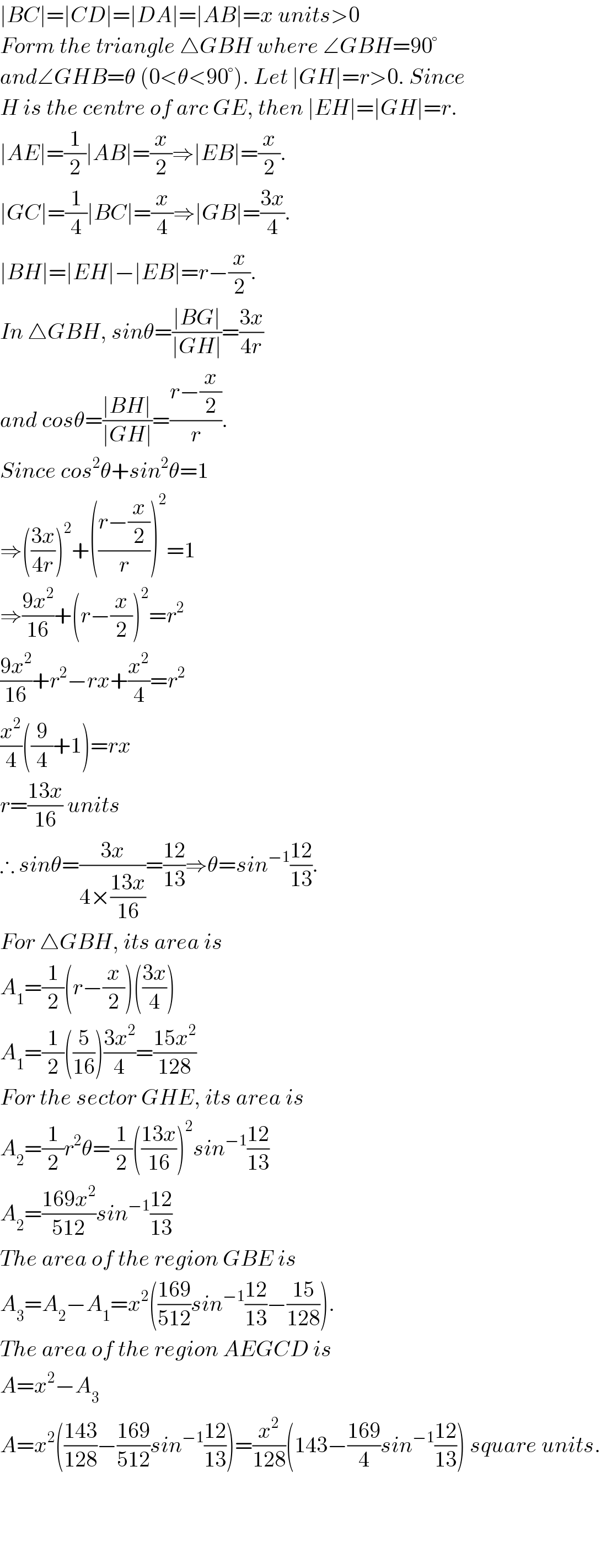
∣BC∣=∣CD∣=∣DA∣=∣AB∣=x units>0 Form the triangle △GBH where ∠GBH=90° and∠GHB=θ (0<θ<90°). Let ∣GH∣=r>0. Since H is the centre of arc GE, then ∣EH∣=∣GH∣=r. ∣AE∣=(1/2)∣AB∣=(x/2)⇒∣EB∣=(x/2). ∣GC∣=(1/4)∣BC∣=(x/4)⇒∣GB∣=((3x)/4). ∣BH∣=∣EH∣−∣EB∣=r−(x/2). In △GBH, sinθ=((∣BG∣)/(∣GH∣))=((3x)/(4r)) and cosθ=((∣BH∣)/(∣GH∣))=((r−(x/2))/r). Since cos^2 θ+sin^2 θ=1 ⇒(((3x)/(4r)))^2 +(((r−(x/2))/r))^2 =1 ⇒((9x^2 )/(16))+(r−(x/2))^2 =r^2 ((9x^2 )/(16))+r^2 −rx+(x^2 /4)=r^2 (x^2 /4)((9/4)+1)=rx r=((13x)/(16)) units ∴ sinθ=((3x)/(4×((13x)/(16))))=((12)/(13))⇒θ=sin^(−1) ((12)/(13)). For △GBH, its area is A_1 =(1/2)(r−(x/2))(((3x)/4)) A_1 =(1/2)((5/(16)))((3x^2 )/4)=((15x^2 )/(128)) For the sector GHE, its area is A_2 =(1/2)r^2 θ=(1/2)(((13x)/(16)))^2 sin^(−1) ((12)/(13)) A_2 =((169x^2 )/(512))sin^(−1) ((12)/(13)) The area of the region GBE is A_3 =A_2 −A_1 =x^2 (((169)/(512))sin^(−1) ((12)/(13))−((15)/(128))). The area of the region AEGCD is A=x^2 −A_3 A=x^2 (((143)/(128))−((169)/(512))sin^(−1) ((12)/(13)))=(x^2 /(128))(143−((169)/4)sin^(−1) ((12)/(13))) square units.

$$\mid{BC}\mid=\mid{CD}\mid=\mid{DA}\mid=\mid{AB}\mid={x}\:{units}>\mathrm{0} \\ $$$${Form}\:{the}\:{triangle}\:\bigtriangleup{GBH}\:{where}\:\angle{GBH}=\mathrm{90}° \\ $$$${and}\angle{GHB}=\theta\:\left(\mathrm{0}<\theta<\mathrm{90}°\right).\:{Let}\:\mid{GH}\mid={r}>\mathrm{0}.\:{Since} \\ $$$${H}\:{is}\:{the}\:{centre}\:{of}\:{arc}\:{GE},\:{then}\:\mid{EH}\mid=\mid{GH}\mid={r}. \\ $$$$\mid{AE}\mid=\frac{\mathrm{1}}{\mathrm{2}}\mid{AB}\mid=\frac{{x}}{\mathrm{2}}\Rightarrow\mid{EB}\mid=\frac{{x}}{\mathrm{2}}. \\ $$$$\mid{GC}\mid=\frac{\mathrm{1}}{\mathrm{4}}\mid{BC}\mid=\frac{{x}}{\mathrm{4}}\Rightarrow\mid{GB}\mid=\frac{\mathrm{3}{x}}{\mathrm{4}}. \\ $$$$\mid{BH}\mid=\mid{EH}\mid−\mid{EB}\mid={r}−\frac{{x}}{\mathrm{2}}. \\ $$$${In}\:\bigtriangleup{GBH},\:{sin}\theta=\frac{\mid{BG}\mid}{\mid{GH}\mid}=\frac{\mathrm{3}{x}}{\mathrm{4}{r}} \\ $$$${and}\:{cos}\theta=\frac{\mid{BH}\mid}{\mid{GH}\mid}=\frac{{r}−\frac{{x}}{\mathrm{2}}}{{r}}. \\ $$$${Since}\:{cos}^{\mathrm{2}} \theta+{sin}^{\mathrm{2}} \theta=\mathrm{1} \\ $$$$\Rightarrow\left(\frac{\mathrm{3}{x}}{\mathrm{4}{r}}\right)^{\mathrm{2}} +\left(\frac{{r}−\frac{{x}}{\mathrm{2}}}{{r}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{16}}+\left({r}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{16}}+{r}^{\mathrm{2}} −{rx}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}={r}^{\mathrm{2}} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\left(\frac{\mathrm{9}}{\mathrm{4}}+\mathrm{1}\right)={rx} \\ $$$${r}=\frac{\mathrm{13}{x}}{\mathrm{16}}\:{units} \\ $$$$\therefore\:{sin}\theta=\frac{\mathrm{3}{x}}{\mathrm{4}×\frac{\mathrm{13}{x}}{\mathrm{16}}}=\frac{\mathrm{12}}{\mathrm{13}}\Rightarrow\theta={sin}^{−\mathrm{1}} \frac{\mathrm{12}}{\mathrm{13}}. \\ $$$${For}\:\bigtriangleup{GBH},\:{its}\:{area}\:{is}\: \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left({r}−\frac{{x}}{\mathrm{2}}\right)\left(\frac{\mathrm{3}{x}}{\mathrm{4}}\right) \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{5}}{\mathrm{16}}\right)\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{15}{x}^{\mathrm{2}} }{\mathrm{128}} \\ $$$${For}\:{the}\:{sector}\:{GHE},\:{its}\:{area}\:{is}\: \\ $$$${A}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} \theta=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{13}{x}}{\mathrm{16}}\right)^{\mathrm{2}} {sin}^{−\mathrm{1}} \frac{\mathrm{12}}{\mathrm{13}} \\ $$$${A}_{\mathrm{2}} =\frac{\mathrm{169}{x}^{\mathrm{2}} }{\mathrm{512}}{sin}^{−\mathrm{1}} \frac{\mathrm{12}}{\mathrm{13}} \\ $$$${The}\:{area}\:{of}\:{the}\:{region}\:{GBE}\:{is} \\ $$$${A}_{\mathrm{3}} ={A}_{\mathrm{2}} −{A}_{\mathrm{1}} ={x}^{\mathrm{2}} \left(\frac{\mathrm{169}}{\mathrm{512}}{sin}^{−\mathrm{1}} \frac{\mathrm{12}}{\mathrm{13}}−\frac{\mathrm{15}}{\mathrm{128}}\right). \\ $$$${The}\:{area}\:{of}\:{the}\:{region}\:{AEGCD}\:{is} \\ $$$${A}={x}^{\mathrm{2}} −{A}_{\mathrm{3}} \\ $$$${A}={x}^{\mathrm{2}} \left(\frac{\mathrm{143}}{\mathrm{128}}−\frac{\mathrm{169}}{\mathrm{512}}{sin}^{−\mathrm{1}} \frac{\mathrm{12}}{\mathrm{13}}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{128}}\left(\mathrm{143}−\frac{\mathrm{169}}{\mathrm{4}}{sin}^{−\mathrm{1}} \frac{\mathrm{12}}{\mathrm{13}}\right)\:{square}\:{units}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 16/Jun/16

NICE! THANKS! Although I thought a different approach, like your approach too.My approach needs some construction lines. So I think your approach is better!

$$\mathfrak{NICE}! \\ $$$$\mathfrak{THANKS}!\:{Although}\:{I}\:{thought}\:{a} \\ $$$${different}\:{approach},\:{like}\:{your} \\ $$$${approach}\:{too}.{My}\:{approach}\:{needs} \\ $$$${some}\:{construction}\:{lines}. \\ $$$${So}\:{I}\:{think}\:{your}\:{approach}\:{is}\:{better}! \\ $$

Commented by Yozzii last updated on 16/Jun/16

I see. I think you should still share your method, just to give an alternative approach.

$${I}\:{see}.\:{I}\:{think}\:{you}\:{should}\:{still} \\ $$$${share}\:{your}\:{method},\:{just}\:{to} \\ $$$${give}\:{an}\:{alternative}\:{approach}. \\ $$

Commented by Rasheed Soomro last updated on 17/Jun/16

Not my entire method is different. Only difference is in computing radius and angle of the sector....

$${Not}\:{my}\:{entire}\:{method}\:{is}\:{different}.\:{Only}\:{difference} \\ $$$${is}\:{in}\:{computing}\:{radius}\:{and}\:{angle}\:{of}\:{the}\:{sector}.... \\ $$

Commented by Yozzii last updated on 17/Jun/16

Ah ok lol.

$${Ah}\:{ok}\:{lol}.\: \\ $$

Commented by Rasheed Soomro last updated on 17/Jun/16

Commented by Rasheed Soomro last updated on 18/Jun/16

The radius and angle of the sector can also be determined in the following way: Construction:Join E and G.Draw perpendicular-bisector of EG. Also join G and H According to Yozzi′s answer ∣EB∣=(1/2)x and ∣BG∣=(3/4)x •So in△EBG, ∣EG∣=(√((x/2)^2 +(3x/4)^2 )) =(√((x^2 /4)+((9x^2 )/(16))))=((√(13))/4)x So, ∣EJ∣=(1/2)∣EG∣=(1/2)(((√(13))/4)x)=((√(13))/8)x [HJ^(↔) is perpendicular bisector] Let ∠GEB=α, cos α=∣EB∣/∣EG∣=((1/2)x)/(((√(13))/4)x)=(2/(√(13))) α=cos^(−1) (2/(√(13))) •Now in △EJH, ∣EJ∣=((√(13))/8)x and α=cos^(−1) (2/(√(13))) cos α=∣EJ∣/∣EH∣ cos (cos^(−1) (2/(√(13))))=((((√(13))/8)x)/r) [let ∣EH∣=r] (2/(√(13)))=(((√(13))x)/(8r)) 16r=13x r=((13)/(16))x Let ∠JHE=β and ∠GHE=θ β=90°−α=90°−cos^(−1) (2/(√(13))) θ=2β=180°−2cos^(−1) (2/(√(13))) For further simplification see YOZZII ′s answer to Q#6183. According to it θ=sin^(−1) (((12)/(13)))

$${The}\:{radius}\:{and}\:{angle}\:{of}\:{the}\:{sector} \\ $$$${can}\:{also}\:{be}\:{determined}\:{in}\:{the}\:{following} \\ $$$${way}: \\ $$$${Construction}:{Join}\:{E}\:{and}\:{G}.{Draw}\: \\ $$$${perpendicular}-{bisector}\:{of}\:{EG}. \\ $$$${Also}\:{join}\:{G}\:{and}\:{H} \\ $$$${According}\:{to}\:{Yozzi}'{s}\:{answer} \\ $$$$\:\:\:\:\:\:\:\:\mid{EB}\mid=\frac{\mathrm{1}}{\mathrm{2}}{x}\:\:{and}\:\:\:\mid{BG}\mid=\frac{\mathrm{3}}{\mathrm{4}}{x} \\ $$$$\bullet{So}\:{in}\bigtriangleup{EBG},\:\:\mid{EG}\mid=\sqrt{\left({x}/\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{3}{x}/\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{16}}}=\frac{\sqrt{\mathrm{13}}}{\mathrm{4}}{x} \\ $$$$\:{So},\:\:\mid{EJ}\mid=\frac{\mathrm{1}}{\mathrm{2}}\mid{EG}\mid=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\sqrt{\mathrm{13}}}{\mathrm{4}}{x}\right)=\frac{\sqrt{\mathrm{13}}}{\mathrm{8}}{x}\:\left[\overset{\leftrightarrow} {{HJ}}\:{is}\:{perpendicular}\:{bisector}\right] \\ $$$${Let}\:\:\angle{GEB}=\alpha,\:\:\:\mathrm{cos}\:\:\alpha=\mid{EB}\mid/\mid{EG}\mid=\left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)/\left(\frac{\sqrt{\mathrm{13}}}{\mathrm{4}}{x}\right)=\frac{\mathrm{2}}{\sqrt{\mathrm{13}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\alpha=\mathrm{cos}^{−\mathrm{1}} \:\frac{\mathrm{2}}{\sqrt{\mathrm{13}}}\: \\ $$$$ \\ $$$$\bullet{Now}\:{in}\:\bigtriangleup{EJH},\:\:\mid{EJ}\mid=\frac{\sqrt{\mathrm{13}}}{\mathrm{8}}{x}\:\:\:{and}\:\:\alpha=\mathrm{cos}^{−\mathrm{1}} \:\frac{\mathrm{2}}{\sqrt{\mathrm{13}}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\alpha=\mid{EJ}\mid/\mid{EH}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\left(\mathrm{cos}^{−\mathrm{1}} \:\frac{\mathrm{2}}{\sqrt{\mathrm{13}}}\right)=\frac{\left(\sqrt{\mathrm{13}}/\mathrm{8}\right){x}}{{r}}\:\:\left[{let}\:\mid{EH}\mid={r}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\sqrt{\mathrm{13}}}=\frac{\sqrt{\mathrm{13}}{x}}{\mathrm{8}{r}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{16}{r}=\mathrm{13}{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{r}=\frac{\mathrm{13}}{\mathrm{16}}{x} \\ $$$${Let}\:\angle{JHE}=\beta\:{and}\:\angle{GHE}=\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\beta=\mathrm{90}°−\alpha=\mathrm{90}°−\mathrm{cos}^{−\mathrm{1}} \:\frac{\mathrm{2}}{\sqrt{\mathrm{13}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\theta=\mathrm{2}\beta=\mathrm{180}°−\mathrm{2cos}^{−\mathrm{1}} \:\frac{\mathrm{2}}{\sqrt{\mathrm{13}}} \\ $$$${For}\:{further}\:{simplification}\:{see}\:\mathcal{YOZZII}\:'{s} \\ $$$${answer}\:{to}\:{Q}#\mathrm{6183}.\:{According}\:{to}\:{it} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\theta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{12}}{\mathrm{13}}\right)\:\: \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com