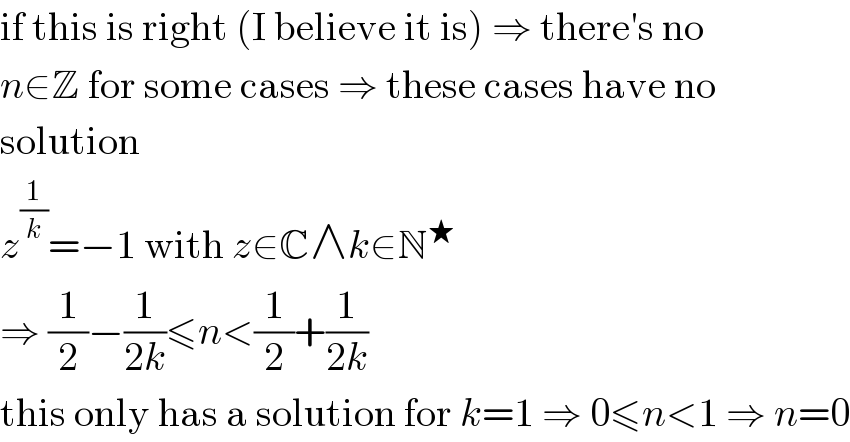Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 61591 by MJS last updated on 05/Jun/19

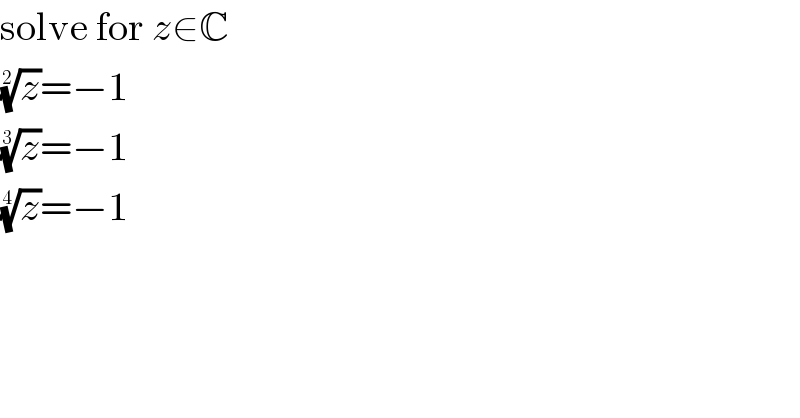
solve for z∈C (z)^(1/2) =−1 (z)^(1/3) =−1 (z)^(1/4) =−1

$$\mathrm{solve}\:\mathrm{for}\:{z}\in\mathbb{C} \\ $$$$\sqrt[{\mathrm{2}}]{{z}}=−\mathrm{1} \\ $$$$\sqrt[{\mathrm{3}}]{{z}}=−\mathrm{1} \\ $$$$\sqrt[{\mathrm{4}}]{{z}}=−\mathrm{1} \\ $$

Commented by Smail last updated on 05/Jun/19

saw (z)^(1/2) ,(z)^(1/3) =−1 and I thought it is (((−1)))^(1/3) and since Iwas solving this problem in a rush I made that silly mistake. My apologies.

$$\:{saw}\:\sqrt[{\mathrm{2}}]{{z}}\:,\sqrt[{\mathrm{3}}]{{z}}=−\mathrm{1}\:{and}\:{I}\:{thought}\:{it}\:{is}\:\sqrt[{\mathrm{3}}]{\left(−\mathrm{1}\right)}\:\:\:{and}\: \\ $$$${since}\:{Iwas}\:{solving}\:{this}\:{problem}\:{in}\:{a}\:{rush} \\ $$$${I}\:{made}\:{that}\:{silly}\:{mistake}. \\ $$$${My}\:{apologies}. \\ $$

Commented by maxmathsup by imad last updated on 05/Jun/19

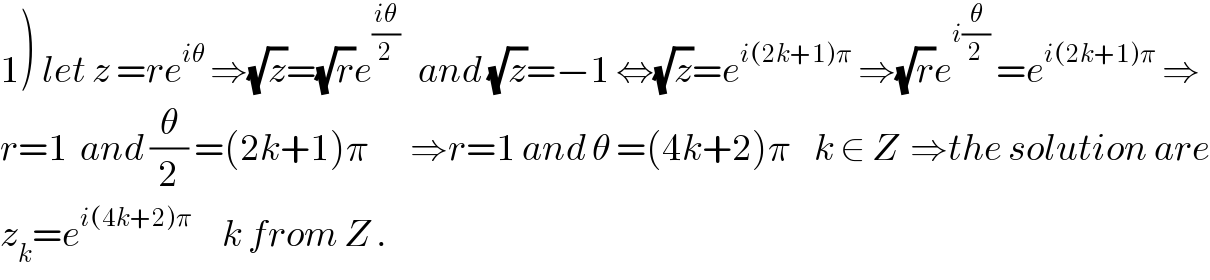
1) let z =re^(iθ) ⇒(√z)=(√r)e^((iθ)/2) and (√z)=−1 ⇔(√z)=e^(i(2k+1)π) ⇒(√r)e^(i(θ/2)) =e^(i(2k+1)π) ⇒ r=1 and (θ/2) =(2k+1)π ⇒r=1 and θ =(4k+2)π k ∈ Z ⇒the solution are z_k =e^(i(4k+2)π) k from Z .

$$\left.\mathrm{1}\right)\:{let}\:{z}\:={re}^{{i}\theta} \:\Rightarrow\sqrt{{z}}=\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} \:\:\:{and}\:\sqrt{{z}}=−\mathrm{1}\:\Leftrightarrow\sqrt{{z}}={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\Rightarrow\sqrt{{r}}{e}^{{i}\frac{\theta}{\mathrm{2}}} \:={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\Rightarrow \\ $$$${r}=\mathrm{1}\:\:{and}\:\frac{\theta}{\mathrm{2}}\:=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\:\:\:\:\:\:\:\Rightarrow{r}=\mathrm{1}\:{and}\:\theta\:=\left(\mathrm{4}{k}+\mathrm{2}\right)\pi\:\:\:\:{k}\:\in\:{Z}\:\:\Rightarrow{the}\:{solution}\:{are} \\ $$$${z}_{{k}} ={e}^{{i}\left(\mathrm{4}{k}+\mathrm{2}\right)\pi} \:\:\:\:\:{k}\:{from}\:{Z}\:. \\ $$

Commented by Mr X pcx last updated on 05/Jun/19

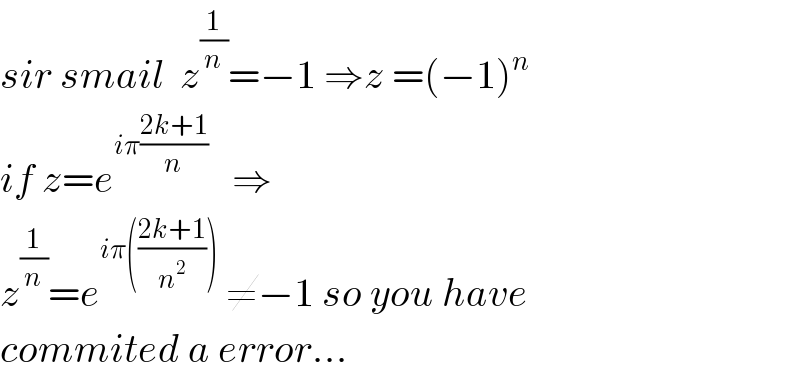
sir smail z^(1/n) =−1 ⇒z =(−1)^n if z=e^(iπ((2k+1)/n)) ⇒ z^(1/n) =e^(iπ(((2k+1)/n^2 ))) ≠−1 so you have commited a error...

$${sir}\:{smail}\:\:{z}^{\frac{\mathrm{1}}{{n}}} =−\mathrm{1}\:\Rightarrow{z}\:=\left(−\mathrm{1}\right)^{{n}} \\ $$$${if}\:{z}={e}^{{i}\pi\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}} \:\:\:\Rightarrow \\ $$$${z}^{\frac{\mathrm{1}}{{n}}} ={e}^{{i}\pi\left(\frac{\mathrm{2}{k}+\mathrm{1}}{{n}^{\mathrm{2}} }\right)} \:\neq−\mathrm{1}\:{so}\:{you}\:{have} \\ $$$${commited}\:{a}\:{error}... \\ $$

Commented by MJS last updated on 05/Jun/19

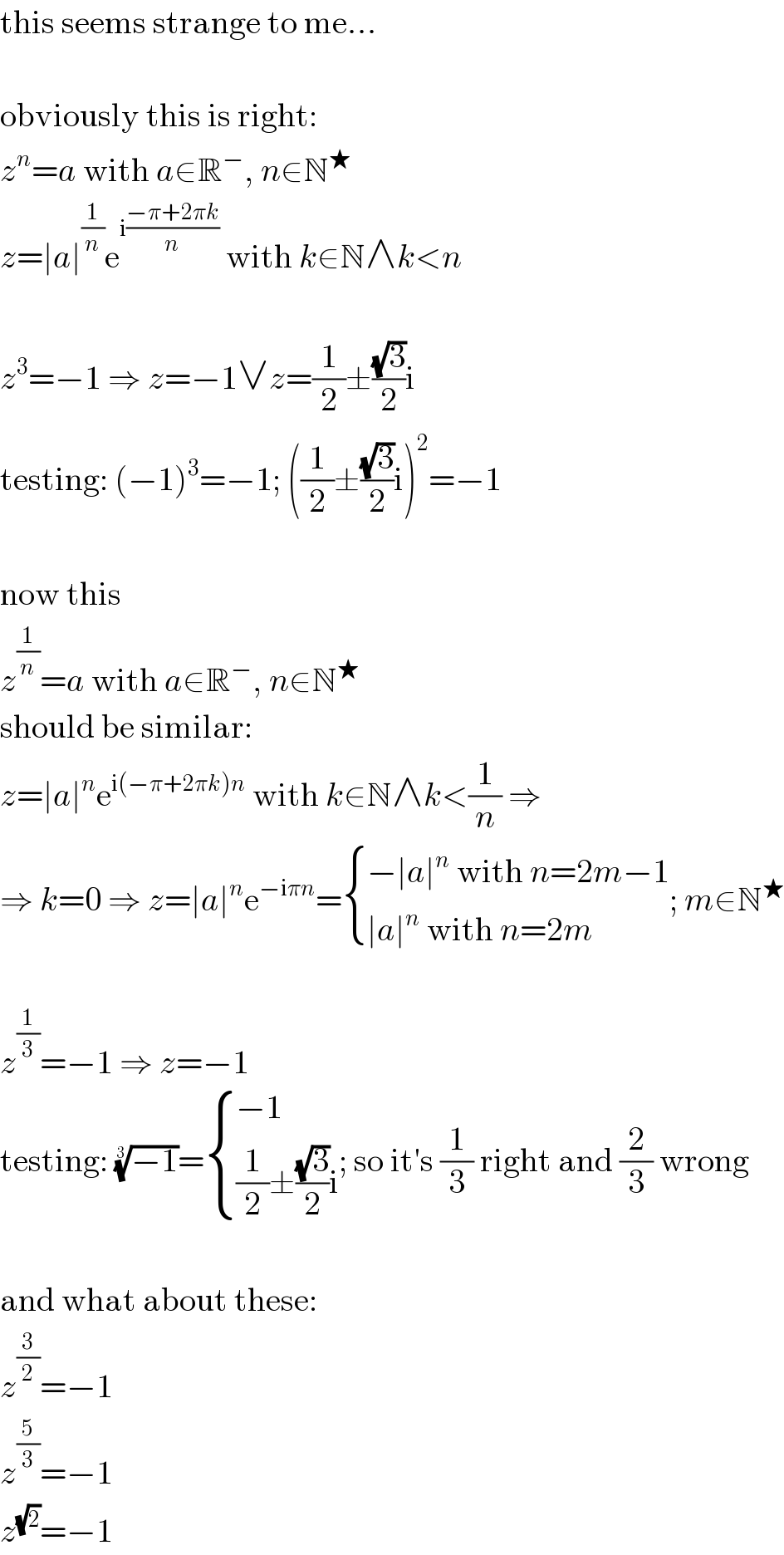
this seems strange to me... obviously this is right: z^n =a with a∈R^− , n∈N^★ z=∣a∣^(1/n) e^(i((−π+2πk)/n)) with k∈N∧k<n z^3 =−1 ⇒ z=−1∨z=(1/2)±((√3)/2)i testing: (−1)^3 =−1; ((1/2)±((√3)/2)i)^2 =−1 now this z^(1/n) =a with a∈R^− , n∈N^★ should be similar: z=∣a∣^n e^(i(−π+2πk)n) with k∈N∧k<(1/n) ⇒ ⇒ k=0 ⇒ z=∣a∣^n e^(−iπn) = { ((−∣a∣^n with n=2m−1)),((∣a∣^n with n=2m)) :}; m∈N^★ z^(1/3) =−1 ⇒ z=−1 testing: ((−1))^(1/3) = { ((−1)),(((1/2)±((√3)/2)i)) :}; so it′s (1/3) right and (2/3) wrong and what about these: z^(3/2) =−1 z^(5/3) =−1 z^(√2) =−1

$$\mathrm{this}\:\mathrm{seems}\:\mathrm{strange}\:\mathrm{to}\:\mathrm{me}... \\ $$$$ \\ $$$$\mathrm{obviously}\:\mathrm{this}\:\mathrm{is}\:\mathrm{right}: \\ $$$${z}^{{n}} ={a}\:\mathrm{with}\:{a}\in\mathbb{R}^{−} ,\:{n}\in\mathbb{N}^{\bigstar} \\ $$$${z}=\mid{a}\mid^{\frac{\mathrm{1}}{{n}}} \mathrm{e}^{\mathrm{i}\frac{−\pi+\mathrm{2}\pi{k}}{{n}}} \:\mathrm{with}\:{k}\in\mathbb{N}\wedge{k}<{n} \\ $$$$ \\ $$$${z}^{\mathrm{3}} =−\mathrm{1}\:\Rightarrow\:{z}=−\mathrm{1}\vee{z}=\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$$\mathrm{testing}:\:\left(−\mathrm{1}\right)^{\mathrm{3}} =−\mathrm{1};\:\left(\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)^{\mathrm{2}} =−\mathrm{1} \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{this} \\ $$$${z}^{\frac{\mathrm{1}}{{n}}} ={a}\:\mathrm{with}\:{a}\in\mathbb{R}^{−} ,\:{n}\in\mathbb{N}^{\bigstar} \\ $$$$\mathrm{should}\:\mathrm{be}\:\mathrm{similar}: \\ $$$${z}=\mid{a}\mid^{{n}} \mathrm{e}^{\mathrm{i}\left(−\pi+\mathrm{2}\pi{k}\right){n}} \:\mathrm{with}\:{k}\in\mathbb{N}\wedge{k}<\frac{\mathrm{1}}{{n}}\:\Rightarrow \\ $$$$\Rightarrow\:{k}=\mathrm{0}\:\Rightarrow\:{z}=\mid{a}\mid^{{n}} \mathrm{e}^{−\mathrm{i}\pi{n}} =\begin{cases}{−\mid{a}\mid^{{n}} \:\mathrm{with}\:{n}=\mathrm{2}{m}−\mathrm{1}}\\{\mid{a}\mid^{{n}} \:\mathrm{with}\:{n}=\mathrm{2}{m}}\end{cases};\:{m}\in\mathbb{N}^{\bigstar} \\ $$$$ \\ $$$${z}^{\frac{\mathrm{1}}{\mathrm{3}}} =−\mathrm{1}\:\Rightarrow\:{z}=−\mathrm{1} \\ $$$$\mathrm{testing}:\:\sqrt[{\mathrm{3}}]{−\mathrm{1}}=\begin{cases}{−\mathrm{1}}\\{\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}}\end{cases};\:\mathrm{so}\:\mathrm{it}'\mathrm{s}\:\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{right}\:\mathrm{and}\:\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{wrong} \\ $$$$ \\ $$$$\mathrm{and}\:\mathrm{what}\:\mathrm{about}\:\mathrm{these}: \\ $$$${z}^{\frac{\mathrm{3}}{\mathrm{2}}} =−\mathrm{1} \\ $$$${z}^{\frac{\mathrm{5}}{\mathrm{3}}} =−\mathrm{1} \\ $$$${z}^{\sqrt{\mathrm{2}}} =−\mathrm{1} \\ $$

Commented by Mr X pcx last updated on 05/Jun/19

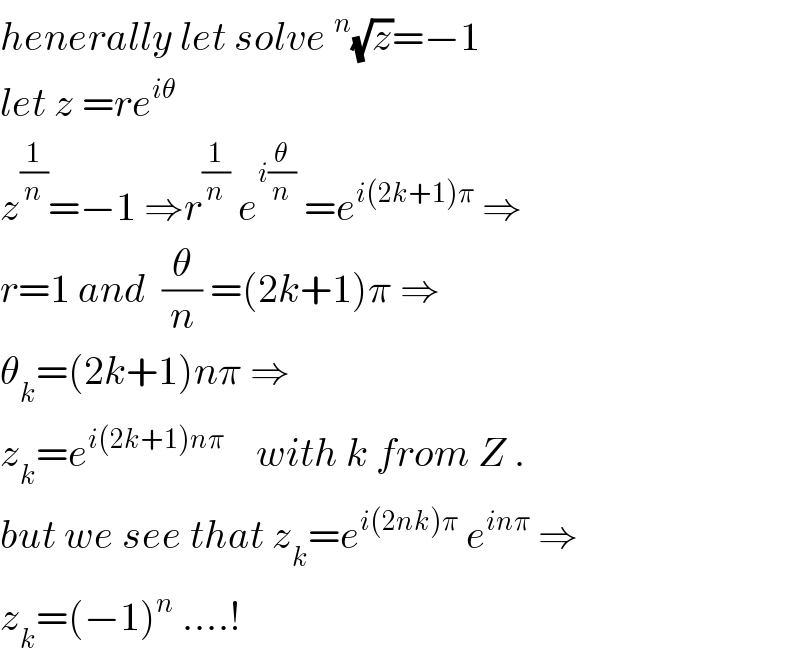
henerally let solve^n (√z)=−1 let z =re^(iθ) z^(1/n) =−1 ⇒r^(1/n) e^(i(θ/n)) =e^(i(2k+1)π) ⇒ r=1 and (θ/n) =(2k+1)π ⇒ θ_k =(2k+1)nπ ⇒ z_k =e^(i(2k+1)nπ) with k from Z . but we see that z_k =e^(i(2nk)π) e^(inπ) ⇒ z_k =(−1)^n ....!

$${henerally}\:{let}\:{solve}\:^{{n}} \sqrt{{z}}=−\mathrm{1} \\ $$$${let}\:{z}\:={re}^{{i}\theta} \:\: \\ $$$${z}^{\frac{\mathrm{1}}{{n}}} =−\mathrm{1}\:\Rightarrow{r}^{\frac{\mathrm{1}}{{n}}} \:{e}^{{i}\frac{\theta}{{n}}} \:={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\Rightarrow \\ $$$${r}=\mathrm{1}\:{and}\:\:\frac{\theta}{{n}}\:=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\:\Rightarrow \\ $$$$\theta_{{k}} =\left(\mathrm{2}{k}+\mathrm{1}\right){n}\pi\:\Rightarrow \\ $$$${z}_{{k}} ={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right){n}\pi} \:\:\:\:{with}\:{k}\:{from}\:{Z}\:. \\ $$$${but}\:{we}\:{see}\:{that}\:{z}_{{k}} ={e}^{{i}\left(\mathrm{2}{nk}\right)\pi} \:{e}^{{in}\pi} \:\Rightarrow \\ $$$${z}_{{k}} =\left(−\mathrm{1}\right)^{{n}} \:....! \\ $$

Commented by Mr X pcx last updated on 05/Jun/19

generally....

$${generally}.... \\ $$

Commented by MJS last updated on 05/Jun/19

I have serious doubts. it seems a matter of definition. if we′re not careful we might end up with (√2)+(√2)=0, not to mention what might happen here: ((−1))^(1/3) +((−1))^(1/3) +((−1))^(1/3) =???

$$\mathrm{I}\:\mathrm{have}\:\mathrm{serious}\:\mathrm{doubts}.\:\mathrm{it}\:\mathrm{seems}\:\mathrm{a}\:\mathrm{matter}\:\mathrm{of} \\ $$$$\mathrm{definition}.\:\mathrm{if}\:\mathrm{we}'\mathrm{re}\:\mathrm{not}\:\mathrm{careful}\:\mathrm{we}\:\mathrm{might}\:\mathrm{end} \\ $$$$\mathrm{up}\:\mathrm{with}\:\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}}=\mathrm{0},\:\mathrm{not}\:\mathrm{to}\:\mathrm{mention}\:\mathrm{what}\:\mathrm{might} \\ $$$$\mathrm{happen}\:\mathrm{here}:\:\sqrt[{\mathrm{3}}]{−\mathrm{1}}+\sqrt[{\mathrm{3}}]{−\mathrm{1}}+\sqrt[{\mathrm{3}}]{−\mathrm{1}}=??? \\ $$

Commented by Smail last updated on 05/Jun/19

I am deleting my answer right now.

$${I}\:{am}\:{deleting}\:{my}\:{answer}\:{right}\:{now}. \\ $$

Answered by MJS last updated on 05/Jun/19

Commented by MJS last updated on 05/Jun/19

if this is right (I believe it is) ⇒ there′s no n∈Z for some cases ⇒ these cases have no solution z^(1/k) =−1 with z∈C∧k∈N^★ ⇒ (1/2)−(1/(2k))≤n<(1/2)+(1/(2k)) this only has a solution for k=1 ⇒ 0≤n<1 ⇒ n=0

$$\mathrm{if}\:\mathrm{this}\:\mathrm{is}\:\mathrm{right}\:\left(\mathrm{I}\:\mathrm{believe}\:\mathrm{it}\:\mathrm{is}\right)\:\Rightarrow\:\mathrm{there}'\mathrm{s}\:\mathrm{no} \\ $$$${n}\in\mathbb{Z}\:\mathrm{for}\:\mathrm{some}\:\mathrm{cases}\:\Rightarrow\:\mathrm{these}\:\mathrm{cases}\:\mathrm{have}\:\mathrm{no} \\ $$$$\mathrm{solution} \\ $$$${z}^{\frac{\mathrm{1}}{{k}}} =−\mathrm{1}\:\mathrm{with}\:{z}\in\mathbb{C}\wedge{k}\in\mathbb{N}^{\bigstar} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}{k}}\leqslant{n}<\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}{k}} \\ $$$$\mathrm{this}\:\mathrm{only}\:\mathrm{has}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{for}\:{k}=\mathrm{1}\:\Rightarrow\:\mathrm{0}\leqslant{n}<\mathrm{1}\:\Rightarrow\:{n}=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com