
Question Number 61601 by Mr X pcx last updated on 05/Jun/19
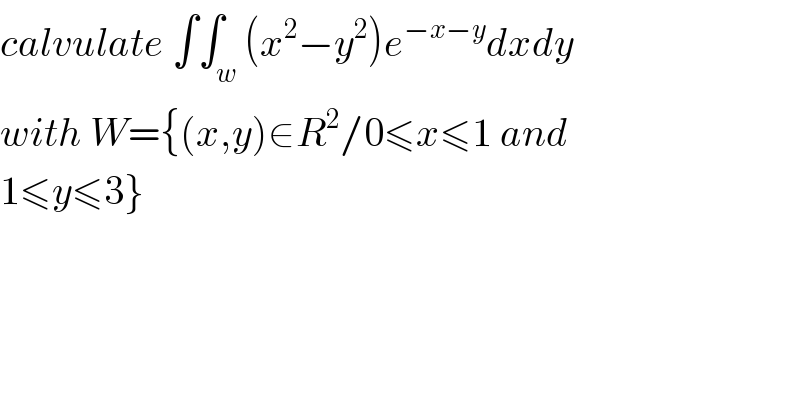
$${calvulate}\:\int\int_{{w}} \left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right){e}^{−{x}−{y}} {dxdy} \\ $$$${with}\:{W}=\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} /\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:{and}\right. \\ $$$$\left.\mathrm{1}\leqslant{y}\leqslant\mathrm{3}\right\} \\ $$
Commented by maxmathsup by imad last updated on 05/Jun/19
![let consider the diffeomorphism (u,v)→ϕ(u,v)=(x ,y) with x−y =u and x+y =v ⇒x =((u+v)/2) and y =((v−u)/2) ⇒ϕ(u,v)=(ϕ_1 ,ϕ_2 ) ϕ_1 (u,v) =(1/2) u +(1/2)v and ϕ_2 (v)=−(1/2) u +(1/2)v 0≤x≤1 and −3≤−y≤ −1 ⇒−3 ≤x−y ≤0 ⇒−3≤u≤0 0≤x≤1 and 1≤y≤3 ⇒ 1≤x+y≤4 ⇒ 1 ≤v≤4 M_j (ϕ) = ((((∂ϕ_1 /∂u) (∂ϕ_1 /∂v))),(((∂ϕ_2 /∂u) (∂ϕ_2 /∂v))) ) = ((((1/2) (1/2))),((−(1/2) (1/2))) ) det M_j =(1/2) ⇒ ∫∫_w (x^2 −y^2 )e^(−x−y) dxdy = ∫∫_(−3≤u≤0 and 1≤v≤4) u.v e^(−v) (1/2) du dv =(1/2) ∫_1 ^4 (∫_(−3) ^0 u du)v e^(−v) dv =(1/2)[(u^2 /2)]_(−3) ^0 ∫_1 ^4 v e^(−v) dv =−(9/4) ∫_1 ^4 v e^(−v) dv by parts ∫_1 ^4 v e^(−v) dv =[−v e^(−v) ]_1 ^4 −∫_1 ^4 −e^(−v) dv = e^(−1) −4 e^(−4) +[−e^(−v) ]_1 ^4 =e^(−1) −4 e^(−4) +e^(−1) −e^(−4) =2e^(−1) −5 e^(−4) ⇒ ∫∫_w (x^2 −y^2 )e^(−x−y) dxdy =−(9/4)(2e^(−1) −5 e^(−4) ) =−(9/2) e^(−1) +((45)/4) e^(−4) =−(9/(2e)) +((45)/(4e^4 )) .](Q61639.png)
$${let}\:{consider}\:{the}\:{diffeomorphism}\:\left({u},{v}\right)\rightarrow\varphi\left({u},{v}\right)=\left({x}\:,{y}\right)\:\:{with}\: \\ $$$${x}−{y}\:={u}\:\:{and}\:{x}+{y}\:={v}\:\Rightarrow{x}\:=\frac{{u}+{v}}{\mathrm{2}}\:\:{and}\:{y}\:=\frac{{v}−{u}}{\mathrm{2}}\:\Rightarrow\varphi\left({u},{v}\right)=\left(\varphi_{\mathrm{1}} ,\varphi_{\mathrm{2}} \right) \\ $$$$\varphi_{\mathrm{1}} \left({u},{v}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:{u}\:+\frac{\mathrm{1}}{\mathrm{2}}{v}\:\:{and}\:\varphi_{\mathrm{2}} \left({v}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\:{u}\:+\frac{\mathrm{1}}{\mathrm{2}}{v} \\ $$$$\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:{and}\:\:\:−\mathrm{3}\leqslant−{y}\leqslant\:−\mathrm{1}\:\Rightarrow−\mathrm{3}\:\leqslant{x}−{y}\:\leqslant\mathrm{0}\:\Rightarrow−\mathrm{3}\leqslant{u}\leqslant\mathrm{0} \\ $$$$\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:{and}\:\mathrm{1}\leqslant{y}\leqslant\mathrm{3}\:\Rightarrow\:\mathrm{1}\leqslant{x}+{y}\leqslant\mathrm{4}\:\Rightarrow\:\mathrm{1}\:\leqslant{v}\leqslant\mathrm{4} \\ $$$${M}_{{j}} \left(\varphi\right)\:=\:\begin{pmatrix}{\frac{\partial\varphi_{\mathrm{1}} }{\partial{u}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\partial\varphi_{\mathrm{1}} }{\partial{v}}}\\{\frac{\partial\varphi_{\mathrm{2}} }{\partial{u}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\partial\varphi_{\mathrm{2}} }{\partial{v}}}\end{pmatrix}\:\:\:\:\:\:=\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}}\\{−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}}\end{pmatrix} \\ $$$${det}\:{M}_{{j}} =\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$$\int\int_{{w}} \left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right){e}^{−{x}−{y}} {dxdy}\:=\:\int\int_{−\mathrm{3}\leqslant{u}\leqslant\mathrm{0}\:{and}\:\mathrm{1}\leqslant{v}\leqslant\mathrm{4}} \:\:\:\:{u}.{v}\:{e}^{−{v}} \:\frac{\mathrm{1}}{\mathrm{2}}\:{du}\:{dv} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{4}} \:\:\left(\int_{−\mathrm{3}} ^{\mathrm{0}} \:\:{u}\:{du}\right){v}\:{e}^{−{v}} \:{dv}\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\right]_{−\mathrm{3}} ^{\mathrm{0}} \:\int_{\mathrm{1}} ^{\mathrm{4}} \:{v}\:{e}^{−{v}} \:{dv} \\ $$$$=−\frac{\mathrm{9}}{\mathrm{4}}\:\int_{\mathrm{1}} ^{\mathrm{4}} \:{v}\:{e}^{−{v}} \:{dv}\:\:\:\:\:{by}\:{parts}\: \\ $$$$\int_{\mathrm{1}} ^{\mathrm{4}} \:{v}\:{e}^{−{v}} \:{dv}\:=\left[−{v}\:{e}^{−{v}} \right]_{\mathrm{1}} ^{\mathrm{4}} \:−\int_{\mathrm{1}} ^{\mathrm{4}} \:−{e}^{−{v}} \:{dv}\:=\:{e}^{−\mathrm{1}} −\mathrm{4}\:{e}^{−\mathrm{4}} \:+\left[−{e}^{−{v}} \right]_{\mathrm{1}} ^{\mathrm{4}} \\ $$$$={e}^{−\mathrm{1}} −\mathrm{4}\:{e}^{−\mathrm{4}} \:+{e}^{−\mathrm{1}} −{e}^{−\mathrm{4}} \:=\mathrm{2}{e}^{−\mathrm{1}} \:−\mathrm{5}\:{e}^{−\mathrm{4}} \:\Rightarrow \\ $$$$\int\int_{{w}} \left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right){e}^{−{x}−{y}} {dxdy}\:=−\frac{\mathrm{9}}{\mathrm{4}}\left(\mathrm{2}{e}^{−\mathrm{1}} −\mathrm{5}\:{e}^{−\mathrm{4}} \right)\:=−\frac{\mathrm{9}}{\mathrm{2}}\:{e}^{−\mathrm{1}} \:+\frac{\mathrm{45}}{\mathrm{4}}\:{e}^{−\mathrm{4}} \\ $$$$=−\frac{\mathrm{9}}{\mathrm{2}{e}}\:+\frac{\mathrm{45}}{\mathrm{4}{e}^{\mathrm{4}} }\:. \\ $$$$ \\ $$
Answered by perlman last updated on 05/Jun/19
![u=x+y.v=x−y x=(u+v)/2 y=((u−v)/2) 0 ≤x≤1 1 ≤y≤3 ==> 1≤x+y≤4........ 1≤u≤4 ==> −3≤x−y≤0........−3≤v≤0 dxdy= [(((∂x/∂u) (∂x/∂v))),(((∂y/∂u) (∂y/∂v))) ]dvdu= determinant ((((1/2) (1/2))),(((1/2) −(1/2)))) dudv=(1/2)dudv (x^2 −y^2 )e^(−(x+y)) dxdy=(x−y)(x+y)e^(−(x+y)) =uve^(−u) ∫∫_w (x^2 −y^2 )e^(−x−y) dxdy=∫_1 ^4 (∫_(−3) ^0 (uv)e^(−u) dv)du=∫_1 ^4 [((uv^2 )/2)e^(−(u)) ]_(−3) ^0 du=∫_1 ^4 9ue^(−u) /2du =(9/2)[−ue^(−u) ]_1 ^4 +(9/2)∫e^(−u) du=((−36e^(−4) )/2)+((9e^(−1) )/2)+(9/2)[−e^(−u) ]_1 ^4 =9e^(−1) −((45)/2)e^(−4)](Q61638.png)
$${u}={x}+{y}.{v}={x}−{y} \\ $$$${x}=\left({u}+{v}\right)/\mathrm{2} \\ $$$${y}=\frac{{u}−{v}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\mathrm{0}\:\leqslant{x}\leqslant\mathrm{1}\:\:\:\:\:\mathrm{1}\:\leqslant{y}\leqslant\mathrm{3} \\ $$$$==>\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\leqslant{x}+{y}\leqslant\mathrm{4}........\:\:\:\:\:\mathrm{1}\leqslant{u}\leqslant\mathrm{4} \\ $$$$==>\:\:\:\:\:\:\:\:−\mathrm{3}\leqslant{x}−{y}\leqslant\mathrm{0}........−\mathrm{3}\leqslant{v}\leqslant\mathrm{0} \\ $$$${dxdy}=\begin{bmatrix}{\frac{\partial{x}}{\partial{u}}\:\:\:\:\:\:\:\:\frac{\partial{x}}{\partial{v}}}\\{\frac{\partial{y}}{\partial{u}}\:\:\:\:\:\:\:\frac{\partial{y}}{\partial{v}}}\end{bmatrix}{dvdu}=\begin{vmatrix}{\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}}\\{\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}}\end{vmatrix}\:{dudv}=\frac{\mathrm{1}}{\mathrm{2}}{dudv} \\ $$$$\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right){e}^{−\left({x}+{y}\right)} {dxdy}=\left({x}−{y}\right)\left({x}+{y}\right){e}^{−\left({x}+{y}\right)} ={uve}^{−{u}} \\ $$$$\int\int_{{w}} \left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right){e}^{−{x}−{y}} {dxdy}=\int_{\mathrm{1}} ^{\mathrm{4}} \left(\int_{−\mathrm{3}} ^{\mathrm{0}} \left({uv}\right){e}^{−{u}} {dv}\right){du}=\int_{\mathrm{1}} ^{\mathrm{4}} \left[\frac{{uv}^{\mathrm{2}} }{\mathrm{2}}{e}^{−\left({u}\right)} \right]_{−\mathrm{3}} ^{\mathrm{0}} {du}=\int_{\mathrm{1}} ^{\mathrm{4}} \mathrm{9}{ue}^{−{u}} /\mathrm{2}{du} \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\left[−{ue}^{−{u}} \right]_{\mathrm{1}} ^{\mathrm{4}} +\frac{\mathrm{9}}{\mathrm{2}}\int{e}^{−{u}} {du}=\frac{−\mathrm{36}{e}^{−\mathrm{4}} }{\mathrm{2}}+\frac{\mathrm{9}{e}^{−\mathrm{1}} }{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{2}}\left[−{e}^{−{u}} \right]_{\mathrm{1}} ^{\mathrm{4}} =\mathrm{9}{e}^{−\mathrm{1}} −\frac{\mathrm{45}}{\mathrm{2}}{e}^{−\mathrm{4}} \\ $$$$ \\ $$
