
Question and Answers Forum
Question Number 61648 by maxmathsup by imad last updated on 05/Jun/19
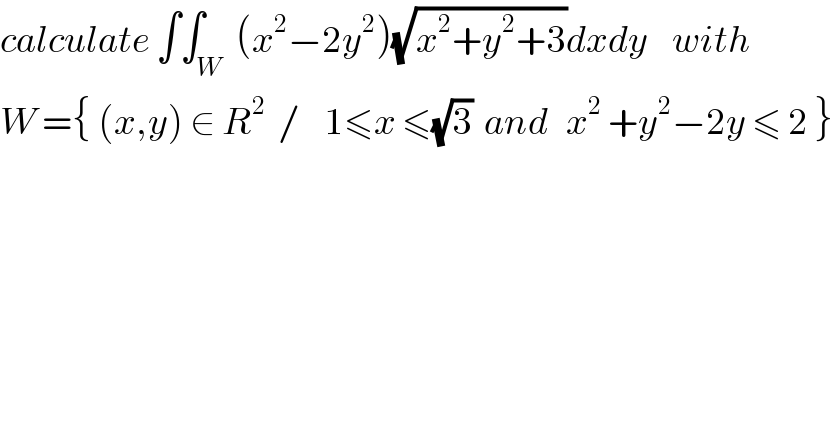
Commented by maxmathsup by imad last updated on 06/Jun/19
![we have x^2 +y^2 −2y ≤2 ⇒x^2 +y^2 −2y +1−1 ≤2 ⇒x^2 +(y−1)^2 ≤3 let use the diffeomorphism x=rcosθ and y−1 =rsinθ we have 1≤x^2 ≤3 ⇒1≤x^2 +(y−1)^2 ≤6 ⇒1≤r^2 ≤6 ⇒1≤r≤(√6) ∫∫_W (x^2 −2y^2 )(√(x^2 +y^2 +3))dxdy =∫∫_(1≤r≤(√6) and −(π/2)≤θ≤(π/2)) (r^2 cos^2 θ−2r^2 sin^2 θ)(√(r^2 +3))rdrdθ =∫_1 ^(√6) r^3 (√(3+r^2 ))dr ∫_(−(π/2)) ^(π/2) (cos^2 θ −2sin^2 θ)dθ ∫_(−(π/2)) ^(π/2) (cos^2 θ −2sin^2 θ)dθ =∫_(−(π/2)) ^(π/2) (((1+cos(2θ))/2) −(1−cos(2θ))dθ =(1/2) ∫_(−((.π)/2)) ^(π/2) (1+cos(2θ)−2 +2cos(2θ))dθ =(1/4) ∫_0 ^(π/2) {3cosθ −1}dθ = (3/4)[sinθ]_0 ^(π/2) −(π/8) =(3/4) −(π/8) . chang.(√(3+r^2 ))=t give 3+r^2 =t^2 ⇒rdr =tdt ∫_1 ^(√6) r^3 (√(3+r^2 ))dr = ∫_2 ^3 (t^2 −3)t dt = ∫_2 ^3 (t^3 −3t)dt =[(1/4)t^4 −(3/2)t^2 ]_2 ^3 =(3^4 /4) −(3^3 /2) −(2^4 /2) +(3/2).2^2 =((81)/4) −((27)/2) −8 +6 =((81−54)/4) −2 =((81−62)/4) =((18)/4) =(9/2) ⇒ ⇒ I = (9/2)((3/4)−(π/8)) =((27)/8) −((9π)/(16)) .](Q61690.png)
| ||
Question and Answers Forum | ||
Question Number 61648 by maxmathsup by imad last updated on 05/Jun/19 | ||
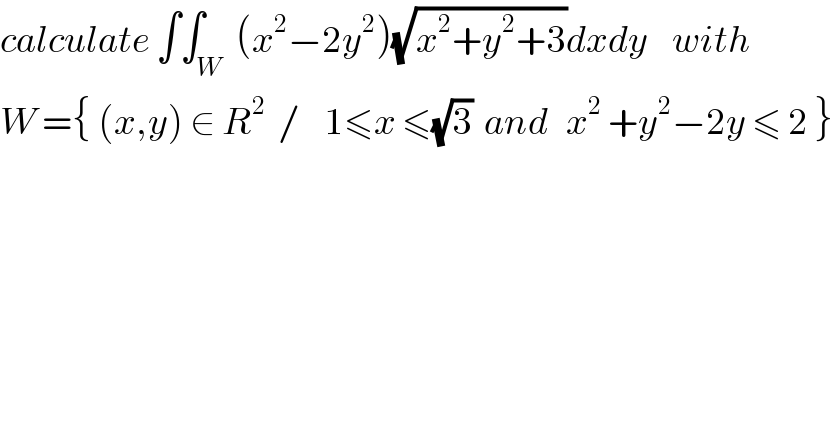 | ||
Commented by maxmathsup by imad last updated on 06/Jun/19 | ||
![we have x^2 +y^2 −2y ≤2 ⇒x^2 +y^2 −2y +1−1 ≤2 ⇒x^2 +(y−1)^2 ≤3 let use the diffeomorphism x=rcosθ and y−1 =rsinθ we have 1≤x^2 ≤3 ⇒1≤x^2 +(y−1)^2 ≤6 ⇒1≤r^2 ≤6 ⇒1≤r≤(√6) ∫∫_W (x^2 −2y^2 )(√(x^2 +y^2 +3))dxdy =∫∫_(1≤r≤(√6) and −(π/2)≤θ≤(π/2)) (r^2 cos^2 θ−2r^2 sin^2 θ)(√(r^2 +3))rdrdθ =∫_1 ^(√6) r^3 (√(3+r^2 ))dr ∫_(−(π/2)) ^(π/2) (cos^2 θ −2sin^2 θ)dθ ∫_(−(π/2)) ^(π/2) (cos^2 θ −2sin^2 θ)dθ =∫_(−(π/2)) ^(π/2) (((1+cos(2θ))/2) −(1−cos(2θ))dθ =(1/2) ∫_(−((.π)/2)) ^(π/2) (1+cos(2θ)−2 +2cos(2θ))dθ =(1/4) ∫_0 ^(π/2) {3cosθ −1}dθ = (3/4)[sinθ]_0 ^(π/2) −(π/8) =(3/4) −(π/8) . chang.(√(3+r^2 ))=t give 3+r^2 =t^2 ⇒rdr =tdt ∫_1 ^(√6) r^3 (√(3+r^2 ))dr = ∫_2 ^3 (t^2 −3)t dt = ∫_2 ^3 (t^3 −3t)dt =[(1/4)t^4 −(3/2)t^2 ]_2 ^3 =(3^4 /4) −(3^3 /2) −(2^4 /2) +(3/2).2^2 =((81)/4) −((27)/2) −8 +6 =((81−54)/4) −2 =((81−62)/4) =((18)/4) =(9/2) ⇒ ⇒ I = (9/2)((3/4)−(π/8)) =((27)/8) −((9π)/(16)) .](Q61690.png) | ||