Question Number 61651 by maxmathsup by imad last updated on 05/Jun/19
![let p(x) =(x+i(√3))^n +(x−i(√3))^n with x real 1) simlify p(x) 2) find the roots of P(x) 3)decompose inside C[x] p(x) 4) calculate ∫_0 ^1 p(x)dx](Q61651.png)
$${let}\:{p}\left({x}\right)\:=\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}} +\left({x}−{i}\sqrt{\mathrm{3}}\right)^{{n}} \:\:\:\:{with}\:{x}\:{real} \\ $$$$\left.\mathrm{1}\right)\:{simlify}\:{p}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{roots}\:{of}\:{P}\left({x}\right) \\ $$$$\left.\mathrm{3}\right){decompose}\:{inside}\:{C}\left[{x}\right]\:\:{p}\left({x}\right) \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} {p}\left({x}\right){dx}\: \\ $$
Commented by maxmathsup by imad last updated on 06/Jun/19
![1) we have P(x) =Σ_(k=0) ^n C_n ^k (i(√3))^k x^(n−k) +Σ_(k=0) ^n C_n ^k (−i(√3))^k x^(n−k) =Σ_(k=0) ^n C_n ^k { i^k +(−i)^k )3^(k/2) x^(n−k) =Σ_(k=2p) (...) +Σ_(k=2p+1) (...) =2Σ_(p=0) ^([(n/2)]) C_n ^(2p) (−1)^p 3^p x^(n−2p) = 2 Σ_(p=0) ^([(n/2)]) (−3)^p C_n ^(2p) x^(n−2p) another way with arctan we have P(x) = 2 Re((x+i(√3))^n ) but ∣x+i(√3)∣ =(√(x^2 +3)) ⇒ x+i(√3)=(√(x^2 +3))((x/(√(x^2 +3))) +i ((√3)/(√(x^(2 ) +3)))) =r e^(iθ) ⇒r =(√(x^2 +3)) and tanθ =((√3)/x) ( we suppose x≠0) ⇒ θ arctan(((√3)/x)) ⇒x+i(√3)=(√(x^2 +3)) e^(iarctan(((√3)/x))) ⇒ (x+i(√3))^n =(x^2 +3)^(n/2) e^(in arctan(((√3)/x))) ⇒P(x) =2(x^2 +3)^(n/2) cos(narctan(((√3)/x)))](Q61702.png)
$$\left.\mathrm{1}\right)\:\:{we}\:{have}\:{P}\left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \left({i}\sqrt{\mathrm{3}}\right)^{{k}} \:{x}^{{n}−{k}} \:+\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \left(−{i}\sqrt{\mathrm{3}}\right)^{{k}} \:{x}^{{n}−{k}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \left\{\:{i}^{{k}} \:+\left(−{i}\right)^{{k}} \right)\mathrm{3}^{\frac{{k}}{\mathrm{2}}} \:{x}^{{n}−{k}} \:=\sum_{{k}=\mathrm{2}{p}} \left(...\right)\:+\sum_{{k}=\mathrm{2}{p}+\mathrm{1}} \left(...\right) \\ $$$$=\mathrm{2}\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\:{C}_{{n}} ^{\mathrm{2}{p}} \:\:\left(−\mathrm{1}\right)^{{p}} \:\mathrm{3}^{{p}} \:{x}^{{n}−\mathrm{2}{p}} \:=\:\mathrm{2}\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \left(−\mathrm{3}\right)^{{p}} \:{C}_{{n}} ^{\mathrm{2}{p}} \:{x}^{{n}−\mathrm{2}{p}} \\ $$$${another}\:{way}\:{with}\:{arctan} \\ $$$${we}\:{have}\:{P}\left({x}\right)\:=\:\mathrm{2}\:{Re}\left(\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}} \right)\:\:\:{but}\:\:\:\:\mid{x}+{i}\sqrt{\mathrm{3}}\mid\:=\sqrt{{x}^{\mathrm{2}} \:+\mathrm{3}}\:\Rightarrow \\ $$$${x}+{i}\sqrt{\mathrm{3}}=\sqrt{{x}^{\mathrm{2}} \:+\mathrm{3}}\left(\frac{{x}}{\sqrt{{x}^{\mathrm{2}} \:+\mathrm{3}}}\:+{i}\:\frac{\sqrt{\mathrm{3}}}{\sqrt{{x}^{\mathrm{2}\:} +\mathrm{3}}}\right)\:={r}\:{e}^{{i}\theta} \:\Rightarrow{r}\:=\sqrt{{x}^{\mathrm{2}} \:+\mathrm{3}}\:\:{and}\:\:{tan}\theta\:=\frac{\sqrt{\mathrm{3}}}{{x}} \\ $$$$\left(\:\:\:{we}\:{suppose}\:{x}\neq\mathrm{0}\right)\:\Rightarrow\:\theta\:{arctan}\left(\frac{\sqrt{\mathrm{3}}}{{x}}\right)\:\Rightarrow{x}+{i}\sqrt{\mathrm{3}}=\sqrt{{x}^{\mathrm{2}} \:+\mathrm{3}}\:{e}^{{iarctan}\left(\frac{\sqrt{\mathrm{3}}}{{x}}\right)} \:\Rightarrow \\ $$$$\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}} \:=\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\frac{{n}}{\mathrm{2}}} \:\:{e}^{{in}\:{arctan}\left(\frac{\sqrt{\mathrm{3}}}{{x}}\right)} \:\Rightarrow{P}\left({x}\right)\:=\mathrm{2}\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\frac{{n}}{\mathrm{2}}} \:{cos}\left({narctan}\left(\frac{\sqrt{\mathrm{3}}}{{x}}\right)\right) \\ $$
Commented by maxmathsup by imad last updated on 06/Jun/19
![2) P(x)=0 ⇔ (x−i(√3))^n =−(x+i(√3))^n ⇔(((x−i(√3))/(x+i(√3))))^n =−1 ⇔ Z^n =−1 with Z =((x−i(√3))/(x+i(√3))) ⇒Zx+i(√3)Z =x−i(√3) ⇒(Z−1)x =−i(√3)Z −i(√3) ⇒ (Z−1)x =−i(√3)(Z+1) ⇒x =i(√3)((1+Z)/(1−Z)) Z^n =−1 ⇒ Z^n =e^(i(2k+1)π) ⇒Z_k =e^(i(((2k+1)π)/n)) and k∈[[0,n−1]] ⇒the roots of P(x) are x_k =i(√3) ((1+e^((i(2k+1)π)/n) )/(1−e^((i(2k+1)π)/n) )) let skmplify x_k x_k =i(√3)((1+cos((2k+1)(π/n))+2i sin((2k+1)(π/(2n)))cos((2k+1)(π/(2n))))/(1−cos((2k+1)(π/n))−2i sin(2k+1)(π/(2n)))cos((2k+1)(π/(2n))))) =i(√3)((2cos^2 ((2k+1)(π/(2n))) +2i sin((2k+1)(π/(2n)))cos((2k+1)(π/(2n))))/(2sin^2 (l2k+1)(π/(2n))−2i sin(2k+1)(π/(2n))) cos(2k+1)(π/(2n)))) =i(√3)((cos(2k+1)(π/(2n))(e^(i(2k+1)(π/(2n))) ))/(−isin(2k+1)(π/(2n))( e^(i(2k+1)(π/(2n))) ))) =−(√3)cotan((2k+1)(π/(2n))) k∈[[0,n−1]] ×](Q61704.png)
$$\left.\mathrm{2}\right)\:{P}\left({x}\right)=\mathrm{0}\:\Leftrightarrow\:\left({x}−{i}\sqrt{\mathrm{3}}\right)^{{n}} \:=−\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}} \:\Leftrightarrow\left(\frac{{x}−{i}\sqrt{\mathrm{3}}}{{x}+{i}\sqrt{\mathrm{3}}}\right)^{{n}} \:=−\mathrm{1}\:\Leftrightarrow\:{Z}^{{n}} \:=−\mathrm{1}\:{with} \\ $$$${Z}\:=\frac{{x}−{i}\sqrt{\mathrm{3}}}{{x}+{i}\sqrt{\mathrm{3}}}\:\Rightarrow{Zx}+{i}\sqrt{\mathrm{3}}{Z}\:={x}−{i}\sqrt{\mathrm{3}}\:\Rightarrow\left({Z}−\mathrm{1}\right){x}\:=−{i}\sqrt{\mathrm{3}}{Z}\:−{i}\sqrt{\mathrm{3}}\:\Rightarrow \\ $$$$\left({Z}−\mathrm{1}\right){x}\:=−{i}\sqrt{\mathrm{3}}\left({Z}+\mathrm{1}\right)\:\Rightarrow{x}\:={i}\sqrt{\mathrm{3}}\frac{\mathrm{1}+{Z}}{\mathrm{1}−{Z}} \\ $$$${Z}^{{n}} \:=−\mathrm{1}\:\Rightarrow\:{Z}^{{n}} \:={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\Rightarrow{Z}_{{k}} ={e}^{{i}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}} \:\:\:{and}\:\:{k}\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right]\:\Rightarrow{the}\:{roots}\:{of}\:{P}\left({x}\right) \\ $$$${are}\:{x}_{{k}} ={i}\sqrt{\mathrm{3}}\:\:\frac{\mathrm{1}+{e}^{\frac{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}} }{\mathrm{1}−{e}^{\frac{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}} }\:\:{let}\:{skmplify}\:\:{x}_{{k}} \\ $$$${x}_{{k}} ={i}\sqrt{\mathrm{3}}\frac{\mathrm{1}+{cos}\left(\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{{n}}\right)+\mathrm{2}{i}\:{sin}\left(\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}\right){cos}\left(\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}\right)}{\left.\mathrm{1}−{cos}\left(\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{{n}}\right)−\mathrm{2}{i}\:{sin}\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}\right){cos}\left(\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}\right)} \\ $$$$={i}\sqrt{\mathrm{3}}\frac{\mathrm{2}{cos}^{\mathrm{2}} \left(\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}\right)\:+\mathrm{2}{i}\:{sin}\left(\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}\right){cos}\left(\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}\right)}{\left.\mathrm{2}{sin}^{\mathrm{2}} \left({l}\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}−\mathrm{2}{i}\:{sin}\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}\right)\:{cos}\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}} \\ $$$$={i}\sqrt{\mathrm{3}}\frac{{cos}\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}\left({e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}} \right)}{−{isin}\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}\left(\:{e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}} \right)}\:=−\sqrt{\mathrm{3}}{cotan}\left(\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}\right)\:\:\:{k}\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right] \\ $$$$× \\ $$
Commented by maxmathsup by imad last updated on 06/Jun/19
$$\left.\mathrm{3}\right)\:{P}\left({x}\right)\:=\lambda\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−{Z}_{{k}} \right)\:=\lambda\:\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}+\sqrt{\mathrm{3}}{cotan}\left(\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}{n}}\right)\right) \\ $$$$\lambda\:{is}\:{thedominent}\:{coefficient}\:\:{of}\:{P}\left({x}\right). \\ $$
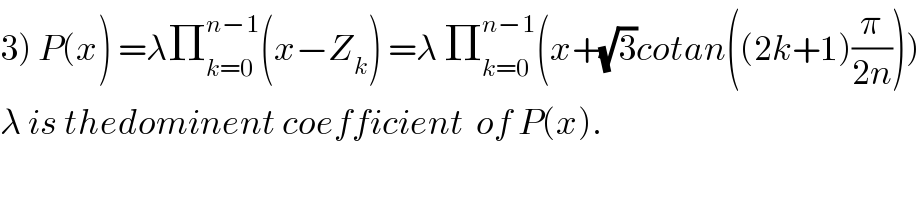
Commented by maxmathsup by imad last updated on 06/Jun/19
![4) we have P(x) =2 Σ_(p=0) ^([(n/2)]) (−3)^p C_n ^(2p) x^(n−2p) ⇒ ∫_0 ^1 P(x)dx =2 Σ_(p=0) ^([(n/2)]) (−3)^p C_n ^(2p) [(1/(n−2p +1))x^(n−2p+1) ]_0 ^1 = 2 Σ_(p=0) ^([(n/2)]) (((−3)^p C_n ^(2p) )/(n−2p+1)) .](Q61712.png)
$$\left.\mathrm{4}\right)\:{we}\:{have}\:{P}\left({x}\right)\:=\mathrm{2}\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \left(−\mathrm{3}\right)^{{p}} \:{C}_{{n}} ^{\mathrm{2}{p}} \:{x}^{{n}−\mathrm{2}{p}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{P}\left({x}\right){dx}\:=\mathrm{2}\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \left(−\mathrm{3}\right)^{{p}} \:{C}_{{n}} ^{\mathrm{2}{p}} \:\:\:\left[\frac{\mathrm{1}}{{n}−\mathrm{2}{p}\:+\mathrm{1}}{x}^{{n}−\mathrm{2}{p}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\:\mathrm{2}\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\:\:\frac{\left(−\mathrm{3}\right)^{{p}} \:{C}_{{n}} ^{\mathrm{2}{p}} }{{n}−\mathrm{2}{p}+\mathrm{1}}\:. \\ $$