
Question and Answers Forum
Question Number 61660 by maxmathsup by imad last updated on 05/Jun/19
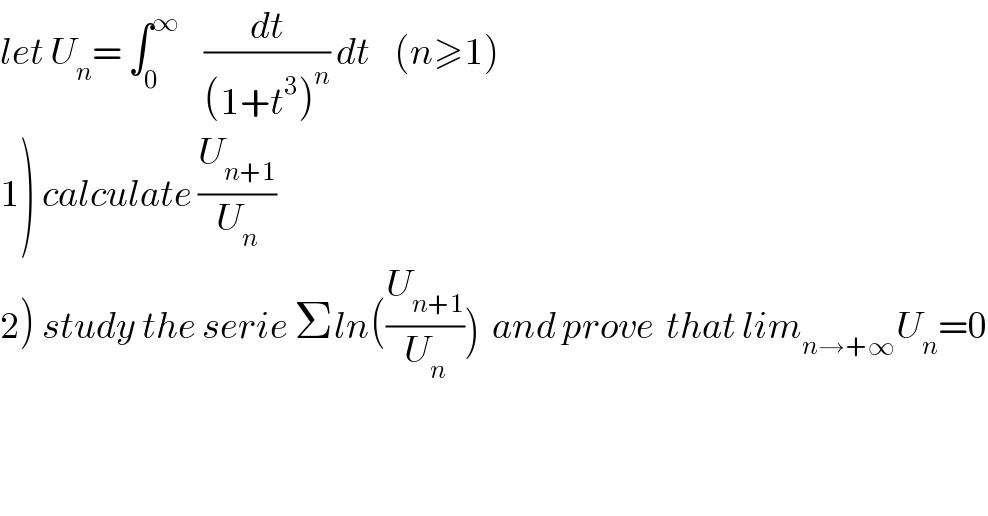
Commented by prof Abdo imad last updated on 07/Jun/19
![1) we have U_n =∫_0 ^∞ ((1+t^3 )/((1+t^3 )^(n+1) )) dt =∫_0 ^∞ (dt/((1+t^3 )^(n+1) )) +∫_0 ^∞ (t^3 /((1+t^3 )^(n+1) )) dt ∫_0 ^∞ (dt/((1+t^3 )^(n+1) )) =U_(n+1) ∫_0 ^∞ (t^3 /((1+t^3 )^(n+1) )) dt = (1/3)∫_0 ^∞ t (3t^2 )(1+t^3 )^(−n−1) dt by parts u =t and v^, =(3t^2 )(1+t^3 )^(−n−1) ⇒ ∫_0 ^∞ (t^3 /((1+t^3 )^(n+1) )) dt = (1/3){ [−(t/n)(1+t^3 )^(−n) ]_0 ^∞ +∫_0 ^∞ (1/n)(1+t^3 )^(−n) dt} =(1/(3n)) ∫_0 ^∞ (dt/((1+t^3 )^n )) =(1/(3n)) U_n ⇒ U_n = U_(n+1) +(1/(3n)) U_n ⇒(1−(1/(3n)))U_n =U_(n+1) ⇒ (((3n−1)/(3n)))U_n =U_(n+1) ⇒(U_(n+1) /U_n ) = 1−(1/(3n))](Q61723.png)
| ||
Question and Answers Forum | ||
Question Number 61660 by maxmathsup by imad last updated on 05/Jun/19 | ||
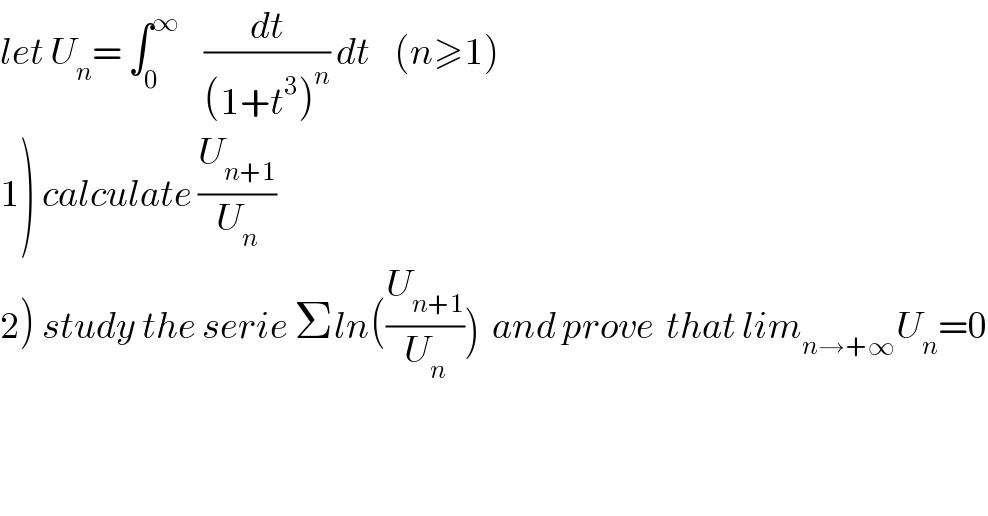 | ||
Commented by prof Abdo imad last updated on 07/Jun/19 | ||
![1) we have U_n =∫_0 ^∞ ((1+t^3 )/((1+t^3 )^(n+1) )) dt =∫_0 ^∞ (dt/((1+t^3 )^(n+1) )) +∫_0 ^∞ (t^3 /((1+t^3 )^(n+1) )) dt ∫_0 ^∞ (dt/((1+t^3 )^(n+1) )) =U_(n+1) ∫_0 ^∞ (t^3 /((1+t^3 )^(n+1) )) dt = (1/3)∫_0 ^∞ t (3t^2 )(1+t^3 )^(−n−1) dt by parts u =t and v^, =(3t^2 )(1+t^3 )^(−n−1) ⇒ ∫_0 ^∞ (t^3 /((1+t^3 )^(n+1) )) dt = (1/3){ [−(t/n)(1+t^3 )^(−n) ]_0 ^∞ +∫_0 ^∞ (1/n)(1+t^3 )^(−n) dt} =(1/(3n)) ∫_0 ^∞ (dt/((1+t^3 )^n )) =(1/(3n)) U_n ⇒ U_n = U_(n+1) +(1/(3n)) U_n ⇒(1−(1/(3n)))U_n =U_(n+1) ⇒ (((3n−1)/(3n)))U_n =U_(n+1) ⇒(U_(n+1) /U_n ) = 1−(1/(3n))](Q61723.png) | ||