
Question and Answers Forum
Question Number 61662 by maxmathsup by imad last updated on 06/Jun/19
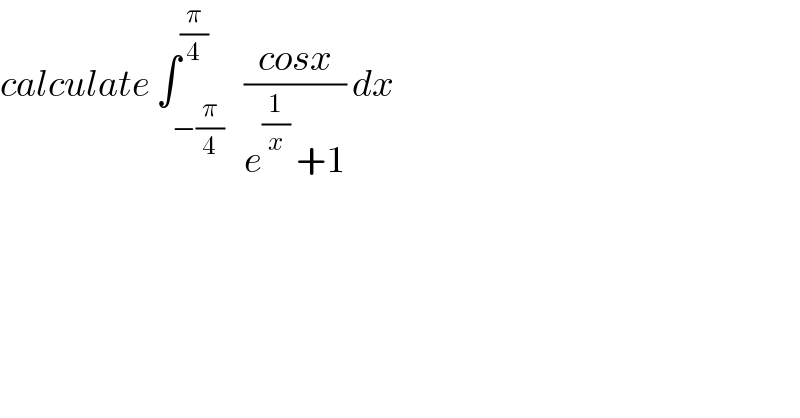
Commented by maxmathsup by imad last updated on 07/Jun/19
![let f(x) =((cosx)/(e^(1/x) +1)) we have the decomposition f(x)=((f(x)+f(−x))/2)(even) +((f(x)−f(−x))/2) (odd) ⇒ I =∫_(−(π/4)) ^(π/4) ((f(x)+f(−x))/2)dx + ∫_(−(π/4)) ^(π/4) ((f(x)−f(−x))/2)dx =H +K K =0 ⇒ I = ∫_0 ^(π/4) {((cos(x))/(e^(1/x) +1)) +((cosx)/(e^(−(1/x)) +1))}dx=∫_0 ^(π/4) {((e^(−(1/x)) +1 +e^(1/x) +1)/(1 +e^(1/x) +e^(−(1/x)) +1))}cosxdx = ∫_0 ^(π/4) cos(x)dx =[sinx]_0 ^(π/4) =((√2)/2) ⇒ I =((√2)/2) .](Q61732.png)
| ||
Question and Answers Forum | ||
Question Number 61662 by maxmathsup by imad last updated on 06/Jun/19 | ||
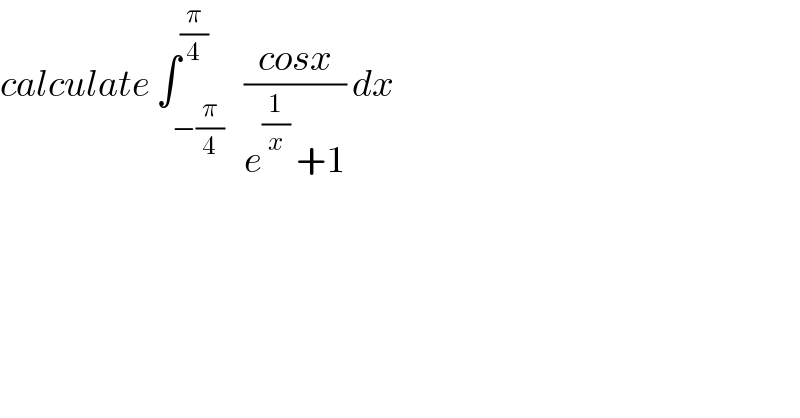 | ||
Commented by maxmathsup by imad last updated on 07/Jun/19 | ||
![let f(x) =((cosx)/(e^(1/x) +1)) we have the decomposition f(x)=((f(x)+f(−x))/2)(even) +((f(x)−f(−x))/2) (odd) ⇒ I =∫_(−(π/4)) ^(π/4) ((f(x)+f(−x))/2)dx + ∫_(−(π/4)) ^(π/4) ((f(x)−f(−x))/2)dx =H +K K =0 ⇒ I = ∫_0 ^(π/4) {((cos(x))/(e^(1/x) +1)) +((cosx)/(e^(−(1/x)) +1))}dx=∫_0 ^(π/4) {((e^(−(1/x)) +1 +e^(1/x) +1)/(1 +e^(1/x) +e^(−(1/x)) +1))}cosxdx = ∫_0 ^(π/4) cos(x)dx =[sinx]_0 ^(π/4) =((√2)/2) ⇒ I =((√2)/2) .](Q61732.png) | ||