
Question Number 61755 by arcana last updated on 08/Jun/19
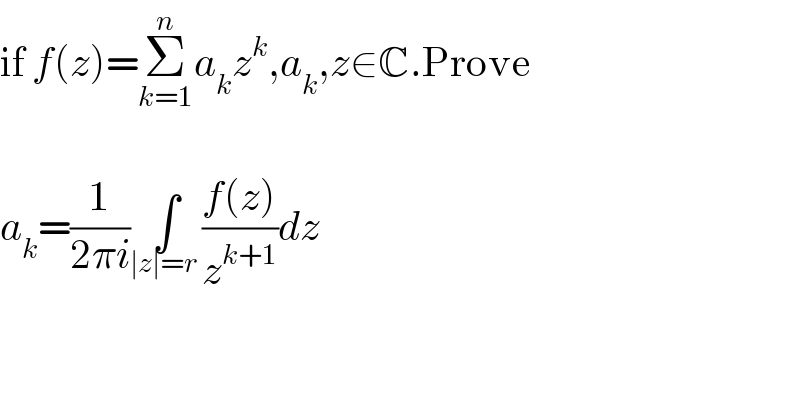
$$\mathrm{if}\:{f}\left({z}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k}} {z}^{{k}} ,{a}_{{k}} ,{z}\in\mathbb{C}.\mathrm{Prove} \\ $$$$ \\ $$$${a}_{{k}} =\frac{\mathrm{1}}{\mathrm{2}\pi{i}}\underset{\mid{z}\mid={r}\:} {\int}\frac{{f}\left({z}\right)}{{z}^{{k}+\mathrm{1}} }{dz} \\ $$$$ \\ $$
Commented by arcana last updated on 08/Jun/19
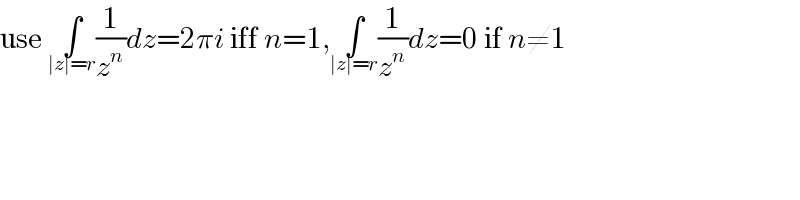
$$\mathrm{use}\:\underset{\mid{z}\mid={r}} {\int}\frac{\mathrm{1}}{{z}^{{n}} }{dz}=\mathrm{2}\pi{i}\:\mathrm{iff}\:{n}=\mathrm{1},\underset{\mid{z}\mid={r}} {\int}\frac{\mathrm{1}}{{z}^{{n}} }{dz}=\mathrm{0}\:\mathrm{if}\:{n}\neq\mathrm{1} \\ $$
Commented by arcana last updated on 09/Jun/19
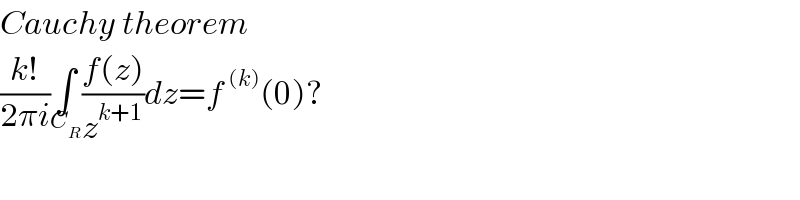
$${Cauchy}\:{theorem} \\ $$$$\frac{{k}!}{\mathrm{2}\pi{i}}\underset{{C}_{{R}} } {\int}\frac{{f}\left({z}\right)}{{z}^{{k}+\mathrm{1}} }{dz}={f}^{\:\left({k}\right)} \left(\mathrm{0}\right)? \\ $$
Answered by perlman last updated on 09/Jun/19
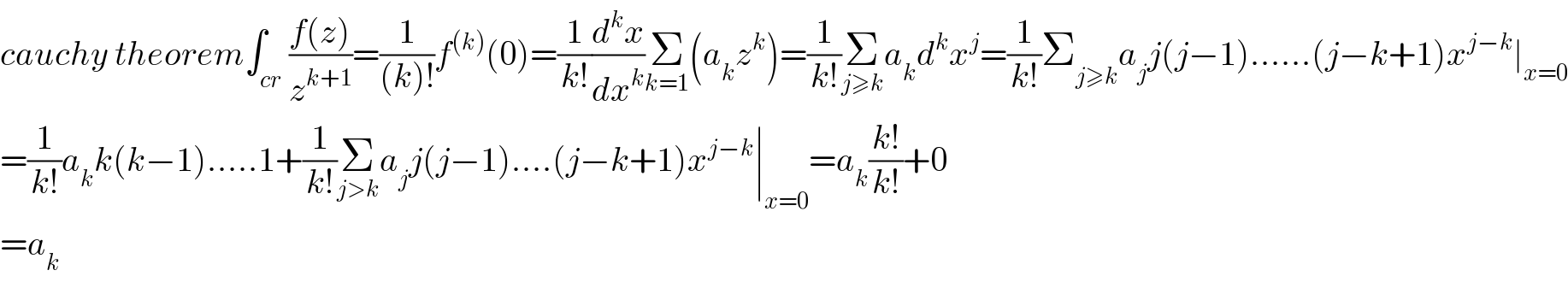
$${cauchy}\:{theorem}\int_{{cr}} \frac{{f}\left({z}\right)}{{z}^{{k}+\mathrm{1}} }=\frac{\mathrm{1}}{\left({k}\right)!}{f}^{\left({k}\right)} \left(\mathrm{0}\right)=\frac{\mathrm{1}}{{k}!}\frac{{d}^{{k}} {x}}{{dx}^{{k}} }\underset{{k}=\mathrm{1}} {\sum}\left({a}_{{k}} {z}^{{k}} \right)=\frac{\mathrm{1}}{{k}!}\underset{{j}\geqslant{k}} {\sum}{a}_{{k}} {d}^{{k}} {x}^{{j}} =\frac{\mathrm{1}}{{k}!}\sum_{{j}\geqslant{k}} {a}_{{j}} {j}\left({j}−\mathrm{1}\right)......\left({j}−{k}+\mathrm{1}\right){x}^{{j}−{k}} \mid_{{x}=\mathrm{0}} \\ $$$$=\frac{\mathrm{1}}{{k}!}{a}_{{k}} {k}\left({k}−\mathrm{1}\right).....\mathrm{1}+\frac{\mathrm{1}}{{k}!}\underset{{j}>{k}} {\sum}{a}_{{j}} {j}\left({j}−\mathrm{1}\right)....\left({j}−{k}+\mathrm{1}\right){x}^{{j}−{k}} \mid_{{x}=\mathrm{0}} ={a}_{{k}} \frac{{k}!}{{k}!}+\mathrm{0} \\ $$$$={a}_{{k}} \\ $$
