Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 61762 by mr W last updated on 08/Jun/19

Commented by mr W last updated on 08/Jun/19

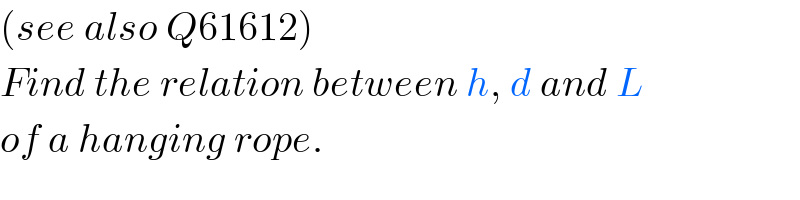
(see also Q61612) Find the relation between h, d and L of a hanging rope.

$$\left({see}\:{also}\:{Q}\mathrm{61612}\right) \\ $$$${Find}\:{the}\:{relation}\:{between}\:{h},\:{d}\:{and}\:{L} \\ $$$${of}\:{a}\:{hanging}\:{rope}. \\ $$

Answered by mr W last updated on 09/Jun/19

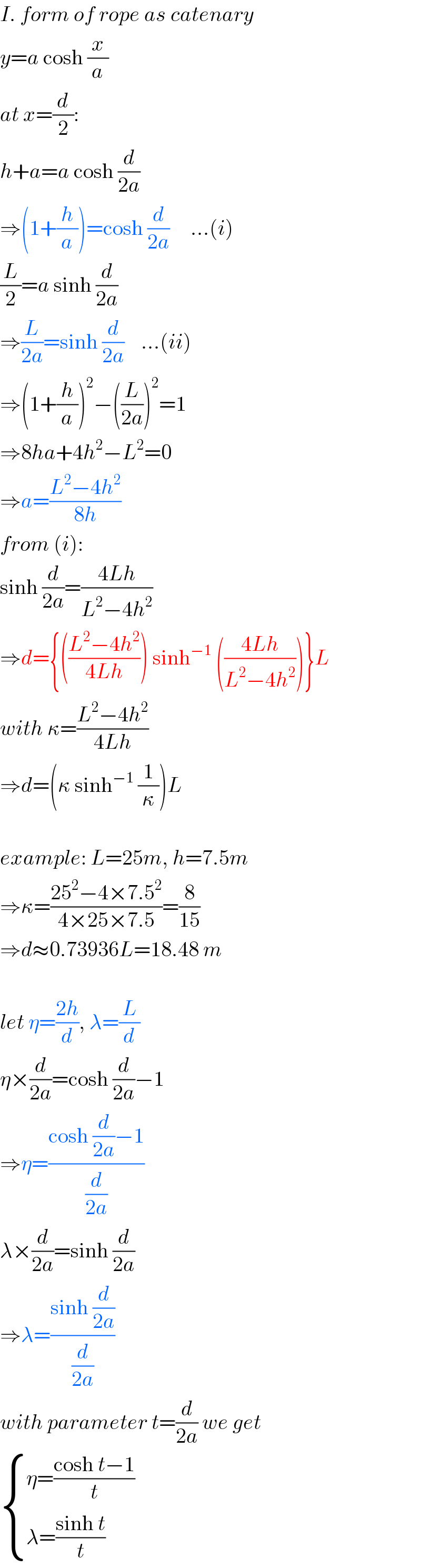
I. form of rope as catenary y=a cosh (x/a) at x=(d/2): h+a=a cosh (d/(2a)) ⇒(1+(h/a))=cosh (d/(2a)) ...(i) (L/2)=a sinh (d/(2a)) ⇒(L/(2a))=sinh (d/(2a)) ...(ii) ⇒(1+(h/a))^2 −((L/(2a)))^2 =1 ⇒8ha+4h^2 −L^2 =0 ⇒a=((L^2 −4h^2 )/(8h)) from (i): sinh (d/(2a))=((4Lh)/(L^2 −4h^2 )) ⇒d={(((L^2 −4h^2 )/(4Lh))) sinh^(−1) (((4Lh)/(L^2 −4h^2 )))}L with κ=((L^2 −4h^2 )/(4Lh)) ⇒d=(κ sinh^(−1) (1/κ))L example: L=25m, h=7.5m ⇒κ=((25^2 −4×7.5^2 )/(4×25×7.5))=(8/(15)) ⇒d≈0.73936L=18.48 m let η=((2h)/d), λ=(L/d) η×(d/(2a))=cosh (d/(2a))−1 ⇒η=((cosh (d/(2a))−1)/(d/(2a))) λ×(d/(2a))=sinh (d/(2a)) ⇒λ=((sinh (d/(2a)))/(d/(2a))) with parameter t=(d/(2a)) we get { ((η=((cosh t−1)/t))),((λ=((sinh t)/t))) :}

$${I}.\:{form}\:{of}\:{rope}\:{as}\:{catenary} \\ $$$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}} \\ $$$${at}\:{x}=\frac{{d}}{\mathrm{2}}: \\ $$$${h}+{a}={a}\:\mathrm{cosh}\:\frac{{d}}{\mathrm{2}{a}} \\ $$$$\Rightarrow\left(\mathrm{1}+\frac{{h}}{{a}}\right)=\mathrm{cosh}\:\frac{{d}}{\mathrm{2}{a}}\:\:\:\:\:...\left({i}\right) \\ $$$$\frac{{L}}{\mathrm{2}}={a}\:\mathrm{sinh}\:\frac{{d}}{\mathrm{2}{a}} \\ $$$$\Rightarrow\frac{{L}}{\mathrm{2}{a}}=\mathrm{sinh}\:\frac{{d}}{\mathrm{2}{a}}\:\:\:\:...\left({ii}\right) \\ $$$$\Rightarrow\left(\mathrm{1}+\frac{{h}}{{a}}\right)^{\mathrm{2}} −\left(\frac{{L}}{\mathrm{2}{a}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\mathrm{8}{ha}+\mathrm{4}{h}^{\mathrm{2}} −{L}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{a}=\frac{{L}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} }{\mathrm{8}{h}} \\ $$$${from}\:\left({i}\right): \\ $$$$\mathrm{sinh}\:\frac{{d}}{\mathrm{2}{a}}=\frac{\mathrm{4}{Lh}}{{L}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} } \\ $$$$\Rightarrow{d}=\left\{\left(\frac{{L}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} }{\mathrm{4}{Lh}}\right)\:\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{\mathrm{4}{Lh}}{{L}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} }\right)\right\}{L} \\ $$$${with}\:\kappa=\frac{{L}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} }{\mathrm{4}{Lh}} \\ $$$$\Rightarrow{d}=\left(\kappa\:\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\kappa}\right){L} \\ $$$$ \\ $$$${example}:\:{L}=\mathrm{25}{m},\:{h}=\mathrm{7}.\mathrm{5}{m} \\ $$$$\Rightarrow\kappa=\frac{\mathrm{25}^{\mathrm{2}} −\mathrm{4}×\mathrm{7}.\mathrm{5}^{\mathrm{2}} }{\mathrm{4}×\mathrm{25}×\mathrm{7}.\mathrm{5}}=\frac{\mathrm{8}}{\mathrm{15}} \\ $$$$\Rightarrow{d}\approx\mathrm{0}.\mathrm{73936}{L}=\mathrm{18}.\mathrm{48}\:{m} \\ $$$$ \\ $$$${let}\:\eta=\frac{\mathrm{2}{h}}{{d}},\:\lambda=\frac{{L}}{{d}} \\ $$$$\eta×\frac{{d}}{\mathrm{2}{a}}=\mathrm{cosh}\:\frac{{d}}{\mathrm{2}{a}}−\mathrm{1} \\ $$$$\Rightarrow\eta=\frac{\mathrm{cosh}\:\frac{{d}}{\mathrm{2}{a}}−\mathrm{1}}{\frac{{d}}{\mathrm{2}{a}}} \\ $$$$\lambda×\frac{{d}}{\mathrm{2}{a}}=\mathrm{sinh}\:\frac{{d}}{\mathrm{2}{a}} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{sinh}\:\frac{{d}}{\mathrm{2}{a}}}{\frac{{d}}{\mathrm{2}{a}}} \\ $$$${with}\:{parameter}\:{t}=\frac{{d}}{\mathrm{2}{a}}\:{we}\:{get}\: \\ $$$$\begin{cases}{\eta=\frac{\mathrm{cosh}\:{t}−\mathrm{1}}{{t}}}\\{\lambda=\frac{\mathrm{sinh}\:{t}}{{t}}}\end{cases} \\ $$

Commented by Tawa1 last updated on 09/Jun/19

wow, God bless you sir

$$\mathrm{wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 08/Jun/19

II. form of rope as parabola y=h(((2x)/d))^2 y′=((8hx)/d^2 ) (L/2)=∫_0 ^(d/2) (√(1+y′^2 )) dx=∫_0 ^(d/2) (√(1+(((8hx)/d^2 ))^2 )) dx L=(d^2 /(4h))∫_0 ^(d/2) (√(1+(((8hx)/d^2 ))^2 )) d(((8hx)/d^2 )) L=(d^2 /(4h))∫_0 ^((4h)/d) (√(1+t^2 )) dt L=2h((d/(4h)))^2 [t(√(1+t^2 ))+ln (t+(√(1+t^2 )))]_0 ^((4h)/d) with μ=((4h)/d) ⇒L=((2h)/μ^2 )[μ(√(1+μ^2 ))+ln (μ+(√(1+μ^2 )))] ⇒(L/(2h))=(1/μ^2 )[μ(√(1+μ^2 ))+ln (μ+(√(1+μ^2 )))] example: L=25m, h=7.5m (1/μ^2 )[μ(√(1+μ^2 ))+ln (μ+(√(1+μ^2 )))]=(5/3) ⇒μ=1.6008 ⇒d=((4h)/μ)=18.74m let η=((2h)/d), λ=(L/d) ⇒λ=(1/(4η))[2η(√(1+4η^2 ))+ln (2η+(√(1+4η^2 )))]

$${II}.\:{form}\:{of}\:{rope}\:{as}\:{parabola} \\ $$$${y}={h}\left(\frac{\mathrm{2}{x}}{{d}}\right)^{\mathrm{2}} \\ $$$${y}'=\frac{\mathrm{8}{hx}}{{d}^{\mathrm{2}} } \\ $$$$\frac{{L}}{\mathrm{2}}=\int_{\mathrm{0}} ^{\frac{{d}}{\mathrm{2}}} \sqrt{\mathrm{1}+{y}'^{\mathrm{2}} }\:{dx}=\int_{\mathrm{0}} ^{\frac{{d}}{\mathrm{2}}} \sqrt{\mathrm{1}+\left(\frac{\mathrm{8}{hx}}{{d}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:{dx} \\ $$$${L}=\frac{{d}^{\mathrm{2}} }{\mathrm{4}{h}}\int_{\mathrm{0}} ^{\frac{{d}}{\mathrm{2}}} \sqrt{\mathrm{1}+\left(\frac{\mathrm{8}{hx}}{{d}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:{d}\left(\frac{\mathrm{8}{hx}}{{d}^{\mathrm{2}} }\right) \\ $$$${L}=\frac{{d}^{\mathrm{2}} }{\mathrm{4}{h}}\int_{\mathrm{0}} ^{\frac{\mathrm{4}{h}}{{d}}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$${L}=\mathrm{2}{h}\left(\frac{{d}}{\mathrm{4}{h}}\right)^{\mathrm{2}} \left[{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{ln}\:\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{4}{h}}{{d}}} \\ $$$${with}\:\mu=\frac{\mathrm{4}{h}}{{d}} \\ $$$$\Rightarrow{L}=\frac{\mathrm{2}{h}}{\mu^{\mathrm{2}} }\left[\mu\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }+\mathrm{ln}\:\left(\mu+\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\right)\right] \\ $$$$\Rightarrow\frac{{L}}{\mathrm{2}{h}}=\frac{\mathrm{1}}{\mu^{\mathrm{2}} }\left[\mu\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }+\mathrm{ln}\:\left(\mu+\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\right)\right] \\ $$$$ \\ $$$${example}:\:{L}=\mathrm{25}{m},\:{h}=\mathrm{7}.\mathrm{5}{m} \\ $$$$\frac{\mathrm{1}}{\mu^{\mathrm{2}} }\left[\mu\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }+\mathrm{ln}\:\left(\mu+\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\right)\right]=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\Rightarrow\mu=\mathrm{1}.\mathrm{6008} \\ $$$$\Rightarrow{d}=\frac{\mathrm{4}{h}}{\mu}=\mathrm{18}.\mathrm{74}{m} \\ $$$$ \\ $$$${let}\:\eta=\frac{\mathrm{2}{h}}{{d}},\:\lambda=\frac{{L}}{{d}} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{1}}{\mathrm{4}\eta}\left[\mathrm{2}\eta\sqrt{\mathrm{1}+\mathrm{4}\eta^{\mathrm{2}} }+\mathrm{ln}\:\left(\mathrm{2}\eta+\sqrt{\mathrm{1}+\mathrm{4}\eta^{\mathrm{2}} }\right)\right] \\ $$

Commented by mr W last updated on 08/Jun/19

Commented by mr W last updated on 08/Jun/19

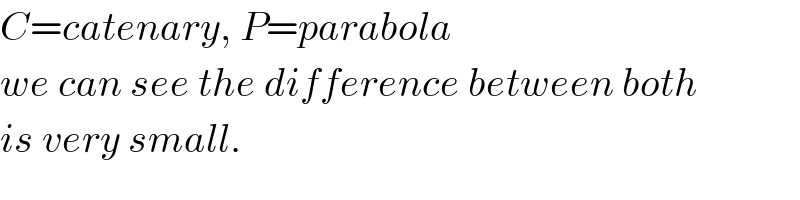
C=catenary, P=parabola we can see the difference between both is very small.

$${C}={catenary},\:{P}={parabola} \\ $$$${we}\:{can}\:{see}\:{the}\:{difference}\:{between}\:{both} \\ $$$${is}\:{very}\:{small}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com