
Question and Answers Forum
Question Number 61840 by psyche last updated on 10/Jun/19

Answered by arcana last updated on 10/Jun/19
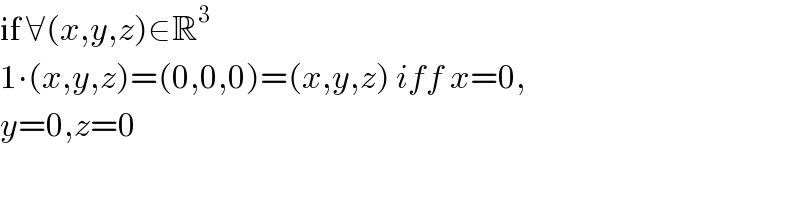
Commented by psyche last updated on 10/Jun/19
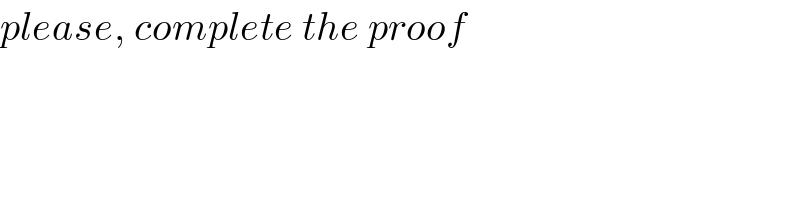
Commented by arcana last updated on 10/Jun/19
![axiom 1,2,3,4 define (R^3 ,“+”) is a structure of group with sum usual in R^3 we need a field K because define ∙ operation. elements in K are scalars, elements inR^3 are vectors if R=K (field) ∙:R×R^3 →R^3 (α,a)→α∙a axiom5 α,β∈R,(x,y,z)∈R^3 α+β∈R ⇒(α+β)∙(x,y,z)=(0,0,0) def. “∙” β∙(x,y,z)=(0,0,0) ; β∙(x,y,z)=(0,0,0) ⇒(α+β)∙(x,y,z)=α∙(x,y,z)+β∙(x,y,z) axiom 6 α∈R,(x,y,z),(x′,y′,z′)∈R^3 α∙[(x,y,z)+(x′,y′,z′)]=α∙(x+x′,y+y′,z+z′) (x+x′,y+y′,z+z′)∈R^3 ⇒α∙(x+x′,y+y′,z+z′)=(0,0,0) α∙[(x,y,z)+(x′,y′,z′)]α∙(x,y,z)=(0,0,0) ; α∙(x′,y′,z′)=(0,0,0) ⇒α∙[(x,y,z)+(x′,y′,z′)]=α∙(x,y,z)+α∙(x′,y′,z′) axiom 7 α,β∈R,(x,y,z)∈R^3 .αβ∈R (αβ)∙(x,y,z)=(0,0,0) β∙(x,y,z)=(0,0,0) ⇒α∙[β∙(x,y,z)]=α∙(0,0,0)=(0,0,0) ⇒(αβ)∙(x,y,z)=α∙[β∙(x,y,z)]](Q61851.png)
| ||
Question and Answers Forum | ||
Question Number 61840 by psyche last updated on 10/Jun/19 | ||
 | ||
Answered by arcana last updated on 10/Jun/19 | ||
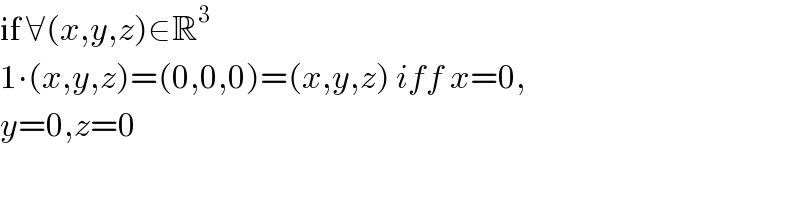 | ||
| ||
Commented by psyche last updated on 10/Jun/19 | ||
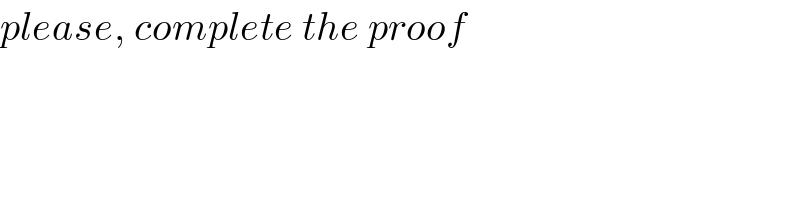 | ||
Commented by arcana last updated on 10/Jun/19 | ||
![axiom 1,2,3,4 define (R^3 ,“+”) is a structure of group with sum usual in R^3 we need a field K because define ∙ operation. elements in K are scalars, elements inR^3 are vectors if R=K (field) ∙:R×R^3 →R^3 (α,a)→α∙a axiom5 α,β∈R,(x,y,z)∈R^3 α+β∈R ⇒(α+β)∙(x,y,z)=(0,0,0) def. “∙” β∙(x,y,z)=(0,0,0) ; β∙(x,y,z)=(0,0,0) ⇒(α+β)∙(x,y,z)=α∙(x,y,z)+β∙(x,y,z) axiom 6 α∈R,(x,y,z),(x′,y′,z′)∈R^3 α∙[(x,y,z)+(x′,y′,z′)]=α∙(x+x′,y+y′,z+z′) (x+x′,y+y′,z+z′)∈R^3 ⇒α∙(x+x′,y+y′,z+z′)=(0,0,0) α∙[(x,y,z)+(x′,y′,z′)]α∙(x,y,z)=(0,0,0) ; α∙(x′,y′,z′)=(0,0,0) ⇒α∙[(x,y,z)+(x′,y′,z′)]=α∙(x,y,z)+α∙(x′,y′,z′) axiom 7 α,β∈R,(x,y,z)∈R^3 .αβ∈R (αβ)∙(x,y,z)=(0,0,0) β∙(x,y,z)=(0,0,0) ⇒α∙[β∙(x,y,z)]=α∙(0,0,0)=(0,0,0) ⇒(αβ)∙(x,y,z)=α∙[β∙(x,y,z)]](Q61851.png) | ||