
Question and Answers Forum
Question Number 61850 by mr W last updated on 10/Jun/19
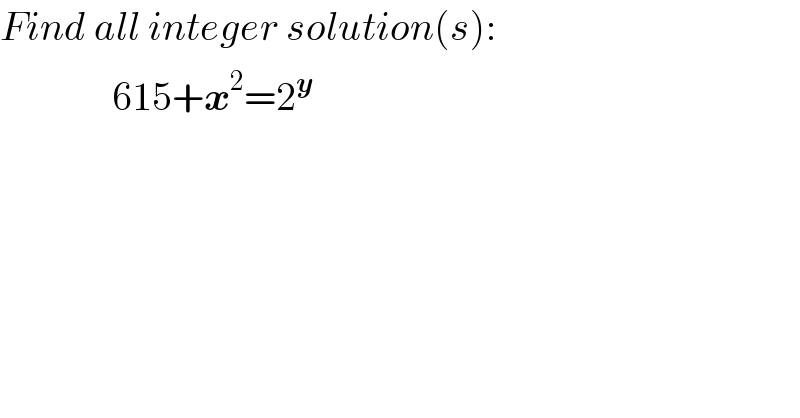
Commented by Rasheed.Sindhi last updated on 10/Jun/19
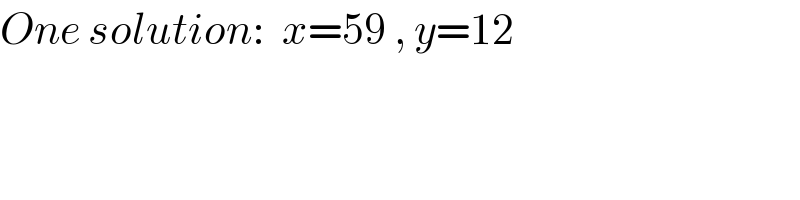
Commented by Rasheed.Sindhi last updated on 11/Jun/19

Commented by mr W last updated on 10/Jun/19

Commented by Rasheed.Sindhi last updated on 11/Jun/19

Commented by Rasheed.Sindhi last updated on 12/Jun/19
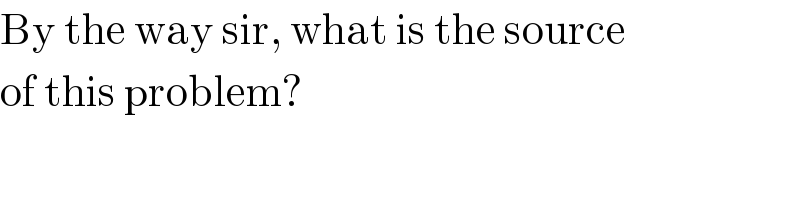
Commented by mr W last updated on 12/Jun/19

Commented by Rasheed.Sindhi last updated on 12/Jun/19
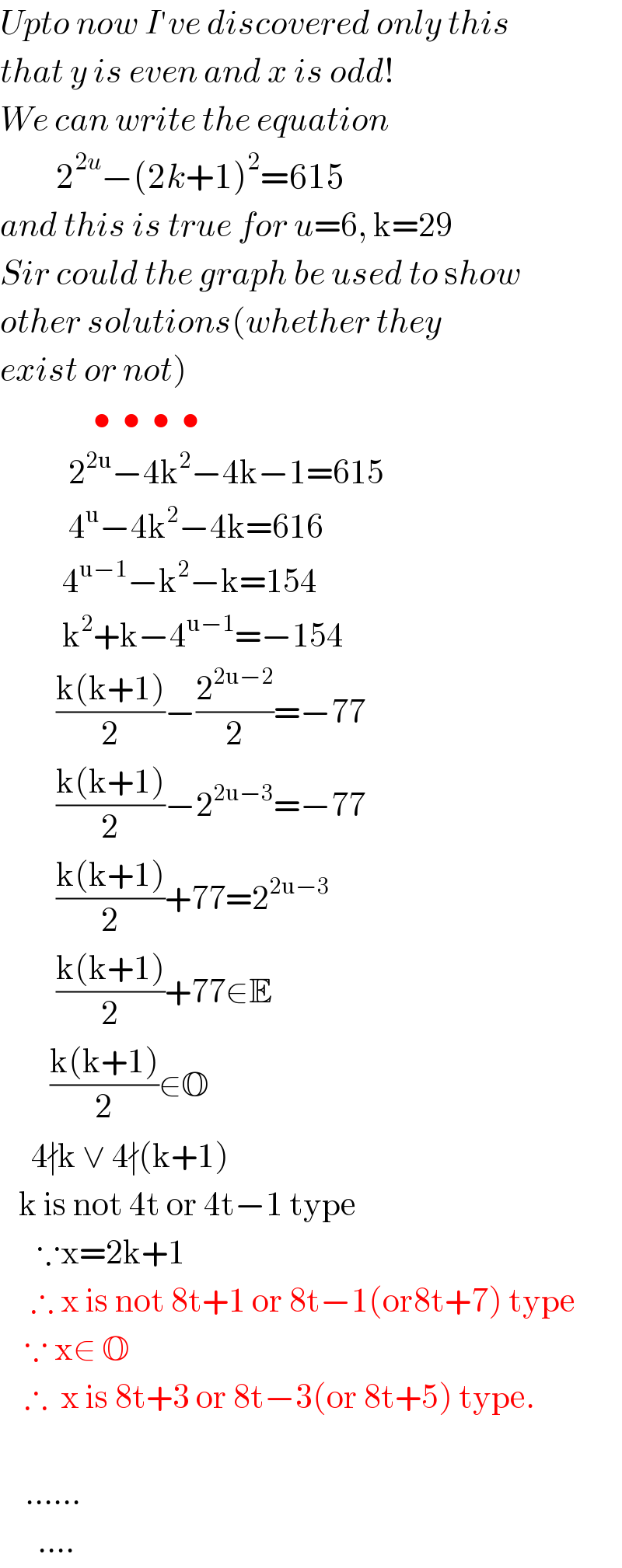
Commented by mr W last updated on 12/Jun/19

Answered by Rasheed.Sindhi last updated on 13/Jun/19
![^(•1) 615+x^2 =2^y ⇒2^y ≥615⇒2^y ≥1024⇒y≥10 ^(•2) 615+x^2 ∈E ⇒x^2 ∈O⇒x∈O ^(•3) 2^y −615=x^2 ⇒2^y −615 is perfect square. ^(•4) 2^y −x^2 =615=3×5×41 ⇒ { ((2^y ≡x^2 (mod 3))),((2^y ≡x^2 (mod 5))),((2^y ≡x^2 (mod 41))) :} ^(•4.1) 2^y ≡x^2 (mod 5) ⇒2^y (mod 5)=x^2 (mod 5) 2^y (mod 5): { ((^( 2^y ) ),2^0 ,2^1 ,2^2 ,2^3 ,2^4 ,2^5 ,2^6 ,(...)),(^(2^y (md 5)) ,1,2,4,3,1,2,4,(...)) :} 2^(4t) ≡1(mod 5)................(ia) 2^(4t+1) ≡2(mod 5)............(iia) 2^(4t+2) ≡4(mod 5)............(iiia) 2^(4t+3) ≡3 (mod 5)............(iva) (Where t∈W) x^2 (mod 5): (x∈O) { (^( x^2 ) ,1^2 ,3^2 ,5^2 ,7^2 ,9^2 ,(11^2 ),(13^2 ),(15^2 ),(...)),(^(x^2 (md 5)) ,1,4,0,4,1,( 1),( 4),( 0),(...)) :} (10k+1)^2 ≡1(mod 5) (10k+3)^2 ≡4(mod 5) (10k+5)^2 ≡0(mod 5) (10k+7)^2 ≡4(mod 5) (10k+9)^2 ≡1(mod 5) 2^(4t) ≡1(mod 5)→ { (((10k+1)^2 ≡1(mod 5))),(((10k+9)^2 ≡1(mod 5))) :} 2^(4t+2) ≡4(mod 5)→ { (((10k+3)^2 ≡4(mod 5))),(((10k+7)^2 ≡4(mod 5))) :} {: (( 2^(4t+1) ≡2(mod 5))),(( 2^(4t+3) ≡3 (mod 5))) } →No x • y is either 4t or 4t+2 type (y∈E) y→4t type, x→10k+1 or 10k+9 type y→4t+2 type, x→10k+3 or 10k+7 type 2^(4t) −(10k+1)^(2 ) =615 ∨ 2^(4t) −(10k+9)^2 =615; t≥3 ,k≥0 _(x=1,11,21,31.... or 9,19,29,39,49,59,69,...)^(y=12,16,20,...) [ y=12 & x=59 satisfy the equation.] 2^(4t+2) −(10k+3)^(2 ) =615 ∨ 2^(4t+2) −(10k+7)^2 =615; t≥2 ,k≥0 _(x=3,13,23,33,.... or 7,17,27,37,...)^(y=10,14,18,22,....) ...... Continue](Q61900.png)
Commented by Rasheed.Sindhi last updated on 11/Jun/19

