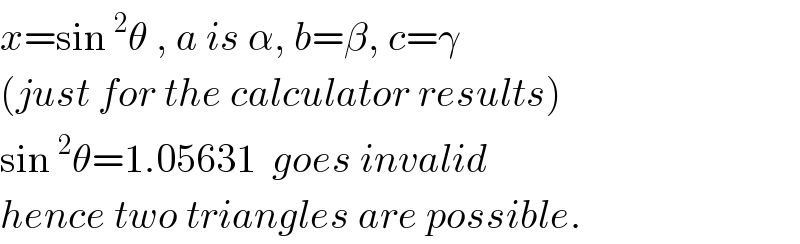Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 61861 by mr W last updated on 10/Jun/19

Commented by mr W last updated on 10/Jun/19

H is the orthocenter of triangle ABC. Its distance to the vertexes is α, β, γ respectively. Find the side lengthes a, b, c of the triangle.

$${H}\:{is}\:{the}\:{orthocenter}\:{of}\:{triangle}\:{ABC}. \\ $$$${Its}\:{distance}\:{to}\:{the}\:{vertexes}\:{is}\:\alpha,\:\beta,\:\gamma \\ $$$${respectively}. \\ $$$${Find}\:{the}\:{side}\:{lengthes}\:{a},\:{b},\:{c}\:{of}\:{the} \\ $$$${triangle}. \\ $$

Commented by MJS last updated on 11/Jun/19

there should be 2 triangles (at least if the triangle is not rectangular). H might be outside the triangle...

$$\mathrm{there}\:\mathrm{should}\:\mathrm{be}\:\mathrm{2}\:\mathrm{triangles}\:\left(\mathrm{at}\:\mathrm{least}\:\mathrm{if}\:\mathrm{the}\right. \\ $$$$\left.\mathrm{triangle}\:\mathrm{is}\:\mathrm{not}\:\mathrm{rectangular}\right).\:{H}\:\mathrm{might}\:\mathrm{be} \\ $$$$\mathrm{outside}\:\mathrm{the}\:\mathrm{triangle}... \\ $$

Commented by MJS last updated on 11/Jun/19

the distances are (1) α=((a(−a^2 +b^2 +c^2 ))/δ) (2) β=((b(a^2 −b^2 +c^2 ))/δ) (3) γ=((c(a^2 +b^2 −c^2 ))/δ) [with δ=(√((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))] we can solve this for given α, β, γ for α=5, β=6, γ=7 I get ((a),(b),(c) ) = (((5.142053)),((3.929466)),((1.562276)) ) ∨ ((a),(b),(c) ) = (((10.94952)),((10.43514)),((9.792451)) ) the 3^(rd) solution is not valid because a, b, c ∉R

$$\mathrm{the}\:\mathrm{distances}\:\mathrm{are} \\ $$$$\left(\mathrm{1}\right)\:\alpha=\frac{{a}\left(−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)}{\delta} \\ $$$$\left(\mathrm{2}\right)\:\beta=\frac{{b}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)}{\delta} \\ $$$$\left(\mathrm{3}\right)\:\gamma=\frac{{c}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)}{\delta} \\ $$$$\:\:\:\:\:\left[\mathrm{with}\:\delta=\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}\right] \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{for}\:\mathrm{given}\:\alpha,\:\beta,\:\gamma \\ $$$$\mathrm{for}\:\alpha=\mathrm{5},\:\beta=\mathrm{6},\:\gamma=\mathrm{7}\:\mathrm{I}\:\mathrm{get} \\ $$$$\begin{pmatrix}{{a}}\\{{b}}\\{{c}}\end{pmatrix}\:=\begin{pmatrix}{\mathrm{5}.\mathrm{142053}}\\{\mathrm{3}.\mathrm{929466}}\\{\mathrm{1}.\mathrm{562276}}\end{pmatrix}\:\vee\:\begin{pmatrix}{{a}}\\{{b}}\\{{c}}\end{pmatrix}\:=\begin{pmatrix}{\mathrm{10}.\mathrm{94952}}\\{\mathrm{10}.\mathrm{43514}}\\{\mathrm{9}.\mathrm{792451}}\end{pmatrix} \\ $$$$\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{solution}\:\mathrm{is}\:\mathrm{not}\:\mathrm{valid}\:\mathrm{because}\:{a},\:{b},\:{c}\:\notin\mathbb{R} \\ $$

Commented by mr W last updated on 12/Jun/19

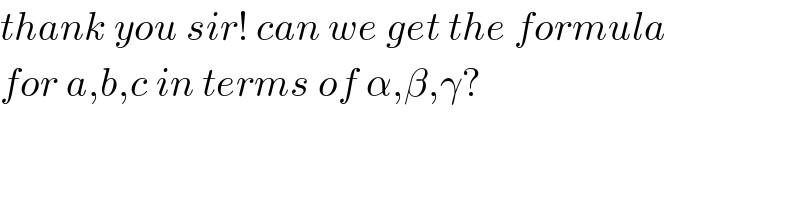
thank you sir! can we get the formula for a,b,c in terms of α,β,γ?

$${thank}\:{you}\:{sir}!\:{can}\:{we}\:{get}\:{the}\:{formula} \\ $$$${for}\:{a},{b},{c}\:{in}\:{terms}\:{of}\:\alpha,\beta,\gamma? \\ $$

Commented by MJS last updated on 12/Jun/19

transformed equations: (1) a^6 +a^4 (α^2 −2(b^2 +c^2 ))−a^2 (2α^2 (b^2 +c^2 )−(b^2 +c^2 )^2 )+α^2 (b^2 −c^2 )^2 =0 (2) b^6 +b^4 (β^2 −2(a^2 +c^2 ))−b^2 (2β^2 (a^2 +c^2 )−(a^2 +c^2 )^2 )+β^2 (a^2 −c^2 )^2 =0 (3) c^6 +c^4 (γ^2 −2(a^2 +b^2 ))−c^2 (2γ^2 (a^2 +b^2 )−(a^2 +b^2 )^2 )+γ^2 (a^2 −b^2 )^2 =0 these are of degree 6 for the leading variable but only of degree 4 for the 2 others. we can omit a^4 from (2) and (3) (2) Aa^4 +... (3) Ba^4 +... B×(2)−A×(3) leads to −4a^2 b^2 c^2 (b^2 −c^2 +β^2 −γ^2 )=0 ⇒ c^2 =b^2 +β^2 −γ^2 now (2)=(3) is of the form Pb^2 +Q=0 ⇒ b^2 =((β^2 (a^2 −β^2 +γ^2 )^2 )/((a+β+γ)(−a+β+γ)(a−β+γ)(a+β−γ))) we are left with (1) which leads to a^(14) +Ba^(12) +Ca^(10) +Da^8 +Ea^6 +Fa^4 +Ga^2 +H=0 a=(√s) s^7 +Bs^6 +Cs^5 +Ds^4 +Es^3 +Fs^2 +Gs+H=0 with H=α^2 (β−γ)^6 (β+γ)^6 . luckily we find that ±(β^2 −γ^2 ) are double zeros each ⇒ s^3 +(α^2 −2(β^2 +γ^2 ))s^2 −(2α^2 (β^2 +γ^2 )−(β^2 +γ^2 )^2 )s+α^2 (β^2 −γ^2 )^2 =0 (which btw looks exactly like the above equations) s=t−((α^2 −2(β^2 +γ^2 ))/3) t^3 −(((α^2 +β^2 +γ^2 )^2 )/3)t+((2(α^2 +β^2 +γ^2 )^3 )/(27))−4α^2 β^2 γ^2 =0 this has got 3 real solutions for α, β, γ ∈R ⇒ we need the trigonometric method which gives no useable general solution in this case

$$\mathrm{transformed}\:\mathrm{equations}: \\ $$$$\left(\mathrm{1}\right)\:\:{a}^{\mathrm{6}} +{a}^{\mathrm{4}} \left(\alpha^{\mathrm{2}} −\mathrm{2}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\right)−{a}^{\mathrm{2}} \left(\mathrm{2}\alpha^{\mathrm{2}} \left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} \right)+\alpha^{\mathrm{2}} \left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\:{b}^{\mathrm{6}} +{b}^{\mathrm{4}} \left(\beta^{\mathrm{2}} −\mathrm{2}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\right)−{b}^{\mathrm{2}} \left(\mathrm{2}\beta^{\mathrm{2}} \left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} \right)+\beta^{\mathrm{2}} \left({a}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\:{c}^{\mathrm{6}} +{c}^{\mathrm{4}} \left(\gamma^{\mathrm{2}} −\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\right)−{c}^{\mathrm{2}} \left(\mathrm{2}\gamma^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} \right)+\gamma^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{these}\:\mathrm{are}\:\mathrm{of}\:\mathrm{degree}\:\mathrm{6}\:\mathrm{for}\:\mathrm{the}\:\mathrm{leading}\:\mathrm{variable} \\ $$$$\mathrm{but}\:\mathrm{only}\:\mathrm{of}\:\mathrm{degree}\:\mathrm{4}\:\mathrm{for}\:\mathrm{the}\:\mathrm{2}\:\mathrm{others}.\:\mathrm{we}\:\mathrm{can} \\ $$$$\mathrm{omit}\:{a}^{\mathrm{4}} \:\mathrm{from}\:\left(\mathrm{2}\right)\:\mathrm{and}\:\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{2}\right)\:{Aa}^{\mathrm{4}} +... \\ $$$$\left(\mathrm{3}\right)\:{Ba}^{\mathrm{4}} +... \\ $$$${B}×\left(\mathrm{2}\right)−{A}×\left(\mathrm{3}\right)\:\mathrm{leads}\:\mathrm{to} \\ $$$$−\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} \left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} +\beta^{\mathrm{2}} −\gamma^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\:{c}^{\mathrm{2}} ={b}^{\mathrm{2}} +\beta^{\mathrm{2}} −\gamma^{\mathrm{2}} \\ $$$$\mathrm{now}\:\left(\mathrm{2}\right)=\left(\mathrm{3}\right)\:\mathrm{is}\:\mathrm{of}\:\mathrm{the}\:\mathrm{form}\:{Pb}^{\mathrm{2}} +{Q}=\mathrm{0} \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} =\frac{\beta^{\mathrm{2}} \left({a}^{\mathrm{2}} −\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)^{\mathrm{2}} }{\left({a}+\beta+\gamma\right)\left(−{a}+\beta+\gamma\right)\left({a}−\beta+\gamma\right)\left({a}+\beta−\gamma\right)} \\ $$$$\mathrm{we}\:\mathrm{are}\:\mathrm{left}\:\mathrm{with}\:\left(\mathrm{1}\right)\:\mathrm{which}\:\mathrm{leads}\:\mathrm{to} \\ $$$${a}^{\mathrm{14}} +\mathcal{B}{a}^{\mathrm{12}} +\mathcal{C}{a}^{\mathrm{10}} +\mathcal{D}{a}^{\mathrm{8}} +\mathcal{E}{a}^{\mathrm{6}} +\mathcal{F}{a}^{\mathrm{4}} +\mathcal{G}{a}^{\mathrm{2}} +\mathcal{H}=\mathrm{0} \\ $$$${a}=\sqrt{{s}} \\ $$$${s}^{\mathrm{7}} +\mathcal{B}{s}^{\mathrm{6}} +\mathcal{C}{s}^{\mathrm{5}} +\mathcal{D}{s}^{\mathrm{4}} +\mathcal{E}{s}^{\mathrm{3}} +\mathcal{F}{s}^{\mathrm{2}} +\mathcal{G}{s}+\mathcal{H}=\mathrm{0} \\ $$$$\mathrm{with}\:\mathcal{H}=\alpha^{\mathrm{2}} \left(\beta−\gamma\right)^{\mathrm{6}} \left(\beta+\gamma\right)^{\mathrm{6}} .\:\mathrm{luckily}\:\mathrm{we}\:\mathrm{find} \\ $$$$\mathrm{that}\:\pm\left(\beta^{\mathrm{2}} −\gamma^{\mathrm{2}} \right)\:\mathrm{are}\:\mathrm{double}\:\mathrm{zeros}\:\mathrm{each}\:\Rightarrow \\ $$$${s}^{\mathrm{3}} +\left(\alpha^{\mathrm{2}} −\mathrm{2}\left(\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)\right){s}^{\mathrm{2}} −\left(\mathrm{2}\alpha^{\mathrm{2}} \left(\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)−\left(\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)^{\mathrm{2}} \right){s}+\alpha^{\mathrm{2}} \left(\beta^{\mathrm{2}} −\gamma^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{which}\:\mathrm{btw}\:\mathrm{looks}\:\mathrm{exactly}\:\mathrm{like}\:\mathrm{the}\:\mathrm{above}\:\mathrm{equations}\right) \\ $$$${s}={t}−\frac{\alpha^{\mathrm{2}} −\mathrm{2}\left(\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)}{\mathrm{3}} \\ $$$${t}^{\mathrm{3}} −\frac{\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{3}}{t}+\frac{\mathrm{2}\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)^{\mathrm{3}} }{\mathrm{27}}−\mathrm{4}\alpha^{\mathrm{2}} \beta^{\mathrm{2}} \gamma^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{has}\:\mathrm{got}\:\mathrm{3}\:\mathrm{real}\:\mathrm{solutions}\:\mathrm{for}\:\alpha,\:\beta,\:\gamma\:\in\mathbb{R} \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{trigonometric}\:\mathrm{method}\:\mathrm{which} \\ $$$$\mathrm{gives}\:\mathrm{no}\:\mathrm{useable}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$

Answered by ajfour last updated on 10/Jun/19

Commented by ajfour last updated on 10/Jun/19

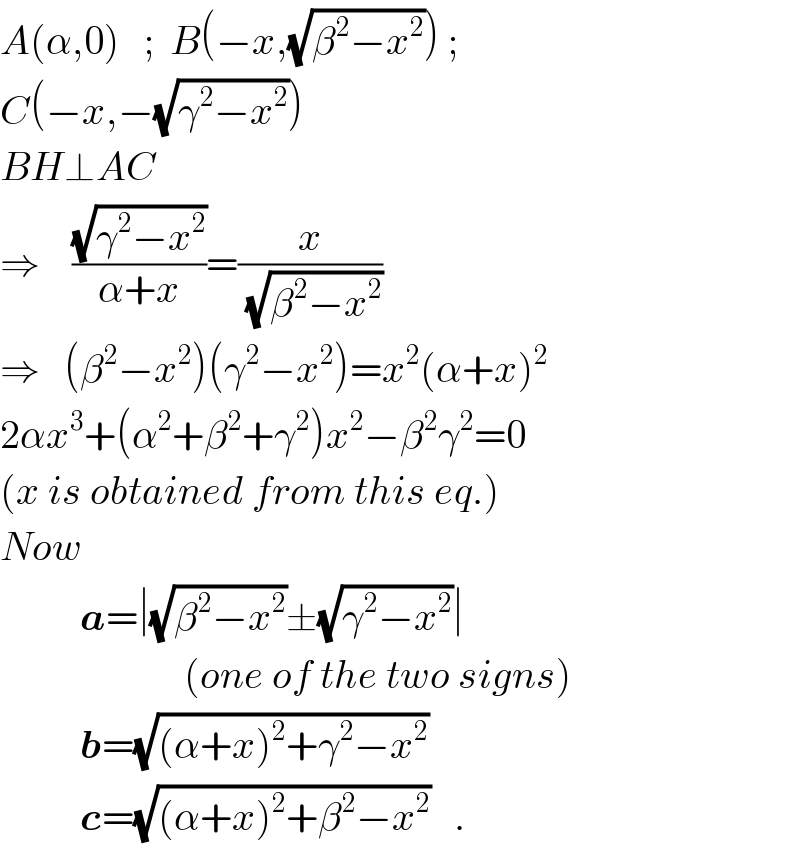
A(α,0) ; B(−x,(√(β^2 −x^2 ))) ; C(−x,−(√(γ^2 −x^2 ))) BH⊥AC ⇒ ((√(γ^2 −x^2 ))/(α+x))=(x/(√(β^2 −x^2 ))) ⇒ (β^2 −x^2 )(γ^2 −x^2 )=x^2 (α+x)^2 2αx^3 +(α^2 +β^2 +γ^2 )x^2 −β^2 γ^2 =0 (x is obtained from this eq.) Now a=∣(√(β^2 −x^2 ))±(√(γ^2 −x^2 ))∣ (one of the two signs) b=(√((α+x)^2 +γ^2 −x^2 )) c=(√((α+x)^2 +β^2 −x^2 )) .

$${A}\left(\alpha,\mathrm{0}\right)\:\:\:;\:\:{B}\left(−{x},\sqrt{\beta^{\mathrm{2}} −{x}^{\mathrm{2}} }\right)\:; \\ $$$${C}\left(−{x},−\sqrt{\gamma^{\mathrm{2}} −{x}^{\mathrm{2}} }\right) \\ $$$${BH}\bot{AC} \\ $$$$\Rightarrow\:\:\:\:\frac{\sqrt{\gamma^{\mathrm{2}} −{x}^{\mathrm{2}} }}{\alpha+{x}}=\frac{{x}}{\sqrt{\beta^{\mathrm{2}} −{x}^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\:\:\left(\beta^{\mathrm{2}} −{x}^{\mathrm{2}} \right)\left(\gamma^{\mathrm{2}} −{x}^{\mathrm{2}} \right)={x}^{\mathrm{2}} \left(\alpha+{x}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}\alpha{x}^{\mathrm{3}} +\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right){x}^{\mathrm{2}} −\beta^{\mathrm{2}} \gamma^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({x}\:{is}\:{obtained}\:{from}\:{this}\:{eq}.\right) \\ $$$${Now}\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\boldsymbol{{a}}=\mid\sqrt{\beta^{\mathrm{2}} −{x}^{\mathrm{2}} }\pm\sqrt{\gamma^{\mathrm{2}} −{x}^{\mathrm{2}} }\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({one}\:{of}\:{the}\:{two}\:{signs}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\boldsymbol{{b}}=\sqrt{\left(\alpha+{x}\right)^{\mathrm{2}} +\gamma^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\boldsymbol{{c}}=\sqrt{\left(\alpha+{x}\right)^{\mathrm{2}} +\beta^{\mathrm{2}} −{x}^{\mathrm{2}} }\:\:\:. \\ $$

Commented by mr W last updated on 10/Jun/19

thank you sir! i tried the same way. but the cubic equation has usually 3 solutions. how can we see which one is the right one? or is the triangle unique?

$${thank}\:{you}\:{sir}!\:{i}\:{tried}\:{the}\:{same}\:{way}. \\ $$$${but}\:{the}\:{cubic}\:{equation}\:{has}\:{usually}\:\mathrm{3} \\ $$$${solutions}.\:{how}\:{can}\:{we}\:{see}\:{which}\:{one} \\ $$$${is}\:{the}\:{right}\:{one}?\:{or}\:{is}\:{the}\:{triangle} \\ $$$${unique}? \\ $$

Answered by mr W last updated on 12/Jun/19

Commented by mr W last updated on 21/Jun/19

assume α≥β≥γ. let HD=u=λα BD=(√(β^2 −u^2 )) DC=(√(γ^2 −u^2 )) ((DC)/(HD))=((AD)/(BD)) ((√(γ^2 −u^2 ))/u)=((u+α)/(√(β^2 −u^2 ))) ⇒(√((β^2 −u^2 )(γ^2 −u^2 )))=u(u+α) ⇒(β^2 −u^2 )(γ^2 −u^2 )=u^2 (u^2 +2αu+α^2 ) ⇒2αu^3 +(α^2 +β^2 +γ^2 )u^2 −β^2 γ^2 =0 ⇒λ^3 +((α^2 +β^2 +γ^2 )/(2α^2 ))λ^2 −((β^2 γ^2 )/(2α^4 ))=0 with q=((α^2 +β^2 +γ^2 )/(6α^2 )), r=((β^2 γ^2 )/(4α^4 )) let p=(r/q^3 )=((54α^2 β^2 γ^2 )/((α^2 +β^2 +γ^2 )^3 ))≤2 ⇒λ^3 +3qλ^2 −2r=0 with λ=s−q ⇒s^3 −3q^2 s+2(q^3 −r)=0 Δ=(−q^2 )^3 +(q^3 −r)^2 =−(2−(r/q^3 ))rq^3 <0 ⇒s=2q sin {(1/3)[sin^(−1) (1−p)+2kπ]}, k=0,1,2 ⇒λ=s−q=q{2 sin [(1/3) sin^(−1) (1−p)+(2/3)kπ]−1}, k=0,1,2 two solutions are suitable: k=0 and 1 ⇒λ=q[2 sin {(1/3) sin^(−1) (1−p)}−1]<0 or ⇒λ=q[2 sin {(1/3) sin^(−1) (1−p)+((2π)/3)}−1]>0 ⇒a=(√(β^2 −λ^2 α^2 ))±(√(γ^2 −λ^2 α^2 )) (−ve for λ<0) ⇒b=(√((1+2λ)α^2 +γ^2 )) ⇒c=(√((1+2λ)α^2 +β^2 )) example: α=7, β=6, γ=5 ⇒λ=0.35604 / −0.597544 ⇒a=9.792451 / 1.562276 ⇒b=10.435137 / 3.929466 ⇒c=10.949525 / 5.142053

$${assume}\:\alpha\geqslant\beta\geqslant\gamma. \\ $$$${let}\:{HD}={u}=\lambda\alpha \\ $$$${BD}=\sqrt{\beta^{\mathrm{2}} −{u}^{\mathrm{2}} } \\ $$$${DC}=\sqrt{\gamma^{\mathrm{2}} −{u}^{\mathrm{2}} } \\ $$$$\frac{{DC}}{{HD}}=\frac{{AD}}{{BD}} \\ $$$$\frac{\sqrt{\gamma^{\mathrm{2}} −{u}^{\mathrm{2}} }}{{u}}=\frac{{u}+\alpha}{\sqrt{\beta^{\mathrm{2}} −{u}^{\mathrm{2}} }} \\ $$$$\Rightarrow\sqrt{\left(\beta^{\mathrm{2}} −{u}^{\mathrm{2}} \right)\left(\gamma^{\mathrm{2}} −{u}^{\mathrm{2}} \right)}={u}\left({u}+\alpha\right) \\ $$$$\Rightarrow\left(\beta^{\mathrm{2}} −{u}^{\mathrm{2}} \right)\left(\gamma^{\mathrm{2}} −{u}^{\mathrm{2}} \right)={u}^{\mathrm{2}} \left({u}^{\mathrm{2}} +\mathrm{2}\alpha{u}+\alpha^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{2}\alpha{u}^{\mathrm{3}} +\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right){u}^{\mathrm{2}} −\beta^{\mathrm{2}} \gamma^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\lambda^{\mathrm{3}} +\frac{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }{\mathrm{2}\alpha^{\mathrm{2}} }\lambda^{\mathrm{2}} −\frac{\beta^{\mathrm{2}} \gamma^{\mathrm{2}} }{\mathrm{2}\alpha^{\mathrm{4}} }=\mathrm{0} \\ $$$${with}\:{q}=\frac{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }{\mathrm{6}\alpha^{\mathrm{2}} },\:{r}=\frac{\beta^{\mathrm{2}} \gamma^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{4}} } \\ $$$${let}\:{p}=\frac{{r}}{{q}^{\mathrm{3}} }=\frac{\mathrm{54}\alpha^{\mathrm{2}} \beta^{\mathrm{2}} \gamma^{\mathrm{2}} }{\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)^{\mathrm{3}} }\leqslant\mathrm{2} \\ $$$$\Rightarrow\lambda^{\mathrm{3}} +\mathrm{3}{q}\lambda^{\mathrm{2}} −\mathrm{2}{r}=\mathrm{0} \\ $$$${with}\:\lambda={s}−{q} \\ $$$$\Rightarrow{s}^{\mathrm{3}} −\mathrm{3}{q}^{\mathrm{2}} {s}+\mathrm{2}\left({q}^{\mathrm{3}} −{r}\right)=\mathrm{0} \\ $$$$\Delta=\left(−{q}^{\mathrm{2}} \right)^{\mathrm{3}} +\left({q}^{\mathrm{3}} −{r}\right)^{\mathrm{2}} =−\left(\mathrm{2}−\frac{{r}}{{q}^{\mathrm{3}} }\right){rq}^{\mathrm{3}} <\mathrm{0} \\ $$$$\Rightarrow{s}=\mathrm{2}{q}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−{p}\right)+\mathrm{2}{k}\pi\right]\right\},\:{k}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$$\Rightarrow\lambda={s}−{q}={q}\left\{\mathrm{2}\:\mathrm{sin}\:\left[\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−{p}\right)+\frac{\mathrm{2}}{\mathrm{3}}{k}\pi\right]−\mathrm{1}\right\},\:{k}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$${two}\:{solutions}\:{are}\:{suitable}:\:{k}=\mathrm{0}\:{and}\:\mathrm{1} \\ $$$$\Rightarrow\lambda={q}\left[\mathrm{2}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−{p}\right)\right\}−\mathrm{1}\right]<\mathrm{0}\:{or} \\ $$$$\Rightarrow\lambda={q}\left[\mathrm{2}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−{p}\right)+\frac{\mathrm{2}\pi}{\mathrm{3}}\right\}−\mathrm{1}\right]>\mathrm{0} \\ $$$$\Rightarrow{a}=\sqrt{\beta^{\mathrm{2}} −\lambda^{\mathrm{2}} \alpha^{\mathrm{2}} }\pm\sqrt{\gamma^{\mathrm{2}} −\lambda^{\mathrm{2}} \alpha^{\mathrm{2}} }\:\:\:\left(−{ve}\:{for}\:\lambda<\mathrm{0}\right) \\ $$$$\Rightarrow{b}=\sqrt{\left(\mathrm{1}+\mathrm{2}\lambda\right)\alpha^{\mathrm{2}} +\gamma^{\mathrm{2}} } \\ $$$$\Rightarrow{c}=\sqrt{\left(\mathrm{1}+\mathrm{2}\lambda\right)\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} } \\ $$$$ \\ $$$${example}:\:\alpha=\mathrm{7},\:\beta=\mathrm{6},\:\gamma=\mathrm{5} \\ $$$$\Rightarrow\lambda=\mathrm{0}.\mathrm{35604}\:/\:−\mathrm{0}.\mathrm{597544} \\ $$$$\Rightarrow{a}=\mathrm{9}.\mathrm{792451}\:/\:\mathrm{1}.\mathrm{562276} \\ $$$$\Rightarrow{b}=\mathrm{10}.\mathrm{435137}\:/\:\mathrm{3}.\mathrm{929466} \\ $$$$\Rightarrow{c}=\mathrm{10}.\mathrm{949525}\:/\:\mathrm{5}.\mathrm{142053} \\ $$

Commented by MJS last updated on 12/Jun/19

yes you′re right

$$\mathrm{yes}\:\mathrm{you}'\mathrm{re}\:\mathrm{right} \\ $$

Answered by ajfour last updated on 12/Jun/19

Commented by mr W last updated on 13/Jun/19

thank you for this new way sir! it seems that all methods lead finally to a cubic equation.

$${thank}\:{you}\:{for}\:{this}\:{new}\:{way}\:{sir}! \\ $$$${it}\:{seems}\:{that}\:{all}\:{methods}\:{lead}\:{finally} \\ $$$${to}\:{a}\:{cubic}\:{equation}. \\ $$

Commented by ajfour last updated on 13/Jun/19

let B origin. H(βcos θ,βsin θ) ....(i) A(βcos θ,βsin θ±α) ...(ii) eq. of AB: y=xcot φ eq. of AC: y=−(x−a)cot θ y_A =x_A cot φ=(a−x_A )cot θ ⇒ x_A =((acot θ)/(cot θ+cot φ))=βcos θ [see (i)] and y_A =x_A cot φ = βsin θ±α [see (ii)] Also βsin θ=γsin φ ⇒ βcos θcot φ=βsin θ±α (βcos θ)(((±(√(1−((β^2 sin^2 θ)/γ^2 ))))/((βsin θ)/γ)))=βsin θ±α let sin^2 θ=t ⇒ (1−t)(γ^2 −β^2 t)=t(β^2 t+α^2 ±2αβ(√t)) ⇒ γ^2 −β^2 t−γ^2 t+β^2 t^2 =β^2 t^2 +α^2 t±2αβt(√t) ⇒ 4α^2 β^2 t^3 =[γ^2 −(α^2 +β^2 +γ^2 )t]^2 or 4α^2 β^2 t^3 −(α^2 +β^2 +γ^2 )^2 t^2 +2γ^2 (α^2 +β^2 +γ^2 )^2 t−γ^4 =0 for α=7, β=6, γ=5 ....

$${let}\:{B}\:{origin}. \\ $$$${H}\left(\beta\mathrm{cos}\:\theta,\beta\mathrm{sin}\:\theta\right)\:\:\:\:....\left({i}\right) \\ $$$${A}\left(\beta\mathrm{cos}\:\theta,\beta\mathrm{sin}\:\theta\pm\alpha\right)\:\:\:\:...\left({ii}\right) \\ $$$${eq}.\:{of}\:{AB}:\:\:\: \\ $$$$\:\:\:{y}={x}\mathrm{cot}\:\phi\:\: \\ $$$${eq}.\:{of}\:{AC}: \\ $$$$\:\:\:{y}=−\left({x}−{a}\right)\mathrm{cot}\:\theta \\ $$$${y}_{{A}} ={x}_{{A}} \mathrm{cot}\:\phi=\left({a}−{x}_{{A}} \right)\mathrm{cot}\:\theta \\ $$$$\Rightarrow\:\:{x}_{{A}} =\frac{{a}\mathrm{cot}\:\theta}{\mathrm{cot}\:\theta+\mathrm{cot}\:\phi}=\beta\mathrm{cos}\:\theta\:\:\:\left[{see}\:\left({i}\right)\right] \\ $$$${and}\:\:{y}_{{A}} ={x}_{{A}} \mathrm{cot}\:\phi\:=\:\beta\mathrm{sin}\:\theta\pm\alpha\:\:\left[{see}\:\left({ii}\right)\right] \\ $$$${Also}\:\:\beta\mathrm{sin}\:\theta=\gamma\mathrm{sin}\:\phi\:\:\: \\ $$$$\Rightarrow\:\:\beta\mathrm{cos}\:\theta\mathrm{cot}\:\phi=\beta\mathrm{sin}\:\theta\pm\alpha \\ $$$$\:\:\:\left(\beta\mathrm{cos}\:\theta\right)\left(\frac{\pm\sqrt{\mathrm{1}−\frac{\beta^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\gamma^{\mathrm{2}} }}}{\frac{\beta\mathrm{sin}\:\theta}{\gamma}}\right)=\beta\mathrm{sin}\:\theta\pm\alpha \\ $$$${let}\:\:\mathrm{sin}\:^{\mathrm{2}} \theta={t} \\ $$$$\Rightarrow\:\:\left(\mathrm{1}−{t}\right)\left(\gamma^{\mathrm{2}} −\beta^{\mathrm{2}} {t}\right)={t}\left(\beta^{\mathrm{2}} {t}+\alpha^{\mathrm{2}} \pm\mathrm{2}\alpha\beta\sqrt{{t}}\right) \\ $$$$\Rightarrow\:\:\gamma^{\mathrm{2}} −\beta^{\mathrm{2}} {t}−\gamma^{\mathrm{2}} {t}+\beta^{\mathrm{2}} {t}^{\mathrm{2}} =\beta^{\mathrm{2}} {t}^{\mathrm{2}} +\alpha^{\mathrm{2}} {t}\pm\mathrm{2}\alpha\beta{t}\sqrt{{t}} \\ $$$$\Rightarrow\:\mathrm{4}\alpha^{\mathrm{2}} \beta^{\mathrm{2}} {t}^{\mathrm{3}} =\left[\gamma^{\mathrm{2}} −\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right){t}\right]^{\mathrm{2}} \\ $$$${or} \\ $$$$\:\:\:\mathrm{4}\alpha^{\mathrm{2}} \beta^{\mathrm{2}} {t}^{\mathrm{3}} −\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)^{\mathrm{2}} {t}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}\gamma^{\mathrm{2}} \left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)^{\mathrm{2}} {t}−\gamma^{\mathrm{4}} =\mathrm{0} \\ $$$${for}\:\alpha=\mathrm{7},\:\beta=\mathrm{6},\:\gamma=\mathrm{5} \\ $$$$.... \\ $$

Commented by ajfour last updated on 13/Jun/19

Commented by ajfour last updated on 13/Jun/19

x=sin^2 θ , a is α, b=β, c=γ (just for the calculator results) sin^2 θ=1.05631 goes invalid hence two triangles are possible.

$${x}=\mathrm{sin}\:^{\mathrm{2}} \theta\:,\:{a}\:{is}\:\alpha,\:{b}=\beta,\:{c}=\gamma \\ $$$$\left({just}\:{for}\:{the}\:{calculator}\:{results}\right) \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \theta=\mathrm{1}.\mathrm{05631}\:\:{goes}\:{invalid} \\ $$$${hence}\:{two}\:{triangles}\:{are}\:{possible}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com