
Question and Answers Forum
Question Number 61976 by maxmathsup by imad last updated on 13/Jun/19
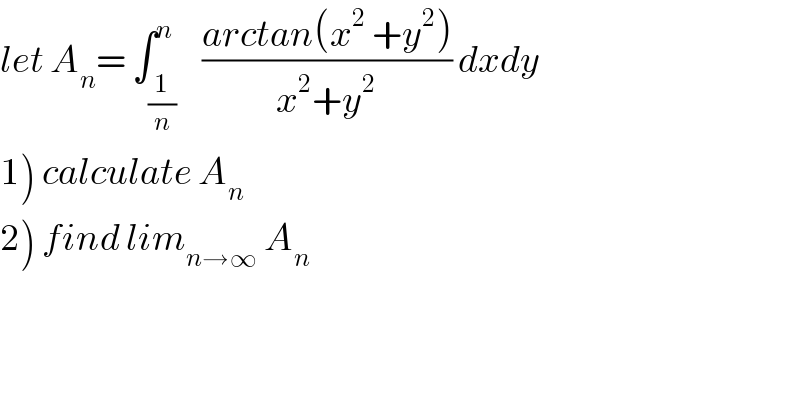
Commented by maxmathsup by imad last updated on 13/Jun/19
,n[^2 ) ((arctan(x^2 +y^2 ))/(x^2 +y^2 ))dxdy](Q61989.png)
Commented by maxmathsup by imad last updated on 14/Jun/19

| ||
Question and Answers Forum | ||
Question Number 61976 by maxmathsup by imad last updated on 13/Jun/19 | ||
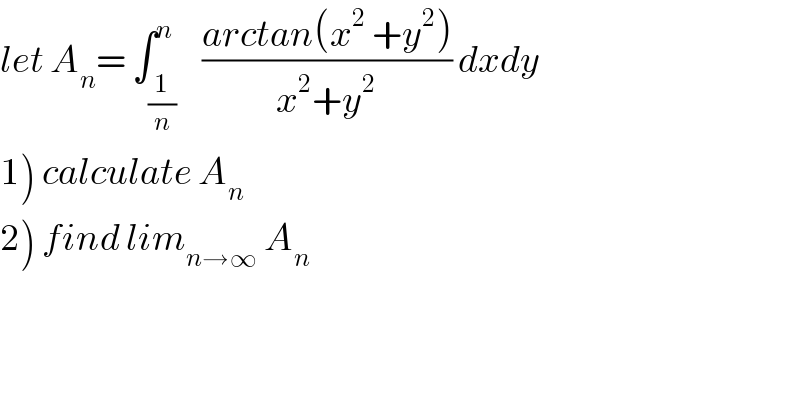 | ||
Commented by maxmathsup by imad last updated on 13/Jun/19 | ||
,n[^2 ) ((arctan(x^2 +y^2 ))/(x^2 +y^2 ))dxdy](Q61989.png) | ||
Commented by maxmathsup by imad last updated on 14/Jun/19 | ||
 | ||