
Question and Answers Forum
Question Number 62077 by naka3546 last updated on 15/Jun/19
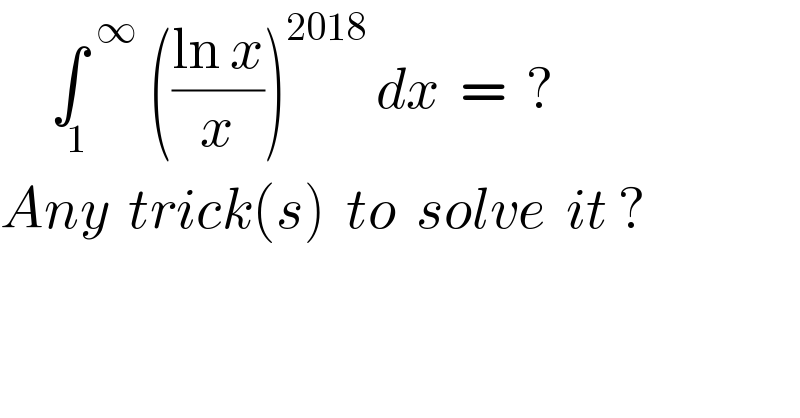
Answered by Smail last updated on 15/Jun/19
![I_n =∫_1 ^∞ (((lnx)/x))^n dx By parts u=ln^n x⇒u′=n((ln^(n−1) x)/x) v′=x^(−n) ⇒v=(x^(1−n) /(1−n)) I_n =(1/(1−n))[((ln^n x)/x^(n−1) )]_1 ^∞ +(n/(n−1))∫_1 ^∞ ((ln^(n−1) x)/x^n )dx =(n/(n−1))∫_1 ^∞ ((ln^(n−1) x)/x^n )dx=(n/(n−1))(((n−1)/(n−1))∫_1 ^∞ ((ln^(n−2) x)/x^n )dx) =((n(n−1)(n−2)...(n−(n−2)))/((n−1)^(n−1) ))∫_1 ^∞ ((ln^(n−(n−1)) x)/x^n )dx =((n(n−1)...2)/((n−1)^(n−1) ))∫_1 ^∞ ((lnx)/x^n )dx ((n!)/((n−1)^n ))∫_1 ^∞ (dx/x^n )=((n!)/((n−1)^n ))[((−1)/((n−1)x^(n−1) ))]_1 ^∞ I_n =((n!)/((n−1)^(n+1) )) For n=2018 I_(2018) =∫_1 ^∞ (((lnx)/x))^(2018) =((2018!)/(2017^(2019) ))](Q62082.png)
| ||
Question and Answers Forum | ||
Question Number 62077 by naka3546 last updated on 15/Jun/19 | ||
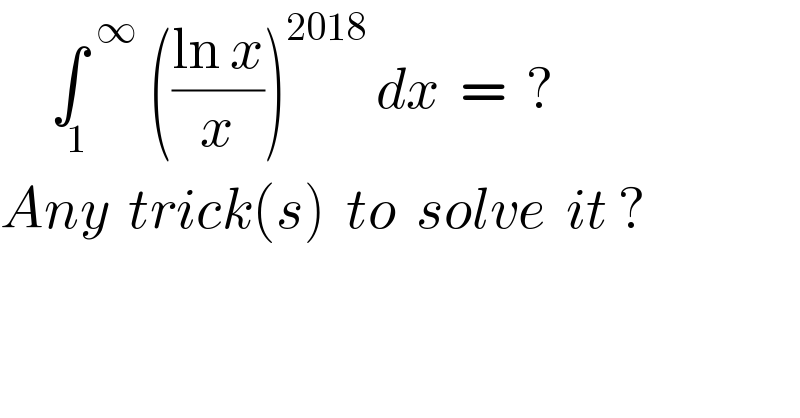 | ||
Answered by Smail last updated on 15/Jun/19 | ||
![I_n =∫_1 ^∞ (((lnx)/x))^n dx By parts u=ln^n x⇒u′=n((ln^(n−1) x)/x) v′=x^(−n) ⇒v=(x^(1−n) /(1−n)) I_n =(1/(1−n))[((ln^n x)/x^(n−1) )]_1 ^∞ +(n/(n−1))∫_1 ^∞ ((ln^(n−1) x)/x^n )dx =(n/(n−1))∫_1 ^∞ ((ln^(n−1) x)/x^n )dx=(n/(n−1))(((n−1)/(n−1))∫_1 ^∞ ((ln^(n−2) x)/x^n )dx) =((n(n−1)(n−2)...(n−(n−2)))/((n−1)^(n−1) ))∫_1 ^∞ ((ln^(n−(n−1)) x)/x^n )dx =((n(n−1)...2)/((n−1)^(n−1) ))∫_1 ^∞ ((lnx)/x^n )dx ((n!)/((n−1)^n ))∫_1 ^∞ (dx/x^n )=((n!)/((n−1)^n ))[((−1)/((n−1)x^(n−1) ))]_1 ^∞ I_n =((n!)/((n−1)^(n+1) )) For n=2018 I_(2018) =∫_1 ^∞ (((lnx)/x))^(2018) =((2018!)/(2017^(2019) ))](Q62082.png) | ||
| ||