
Question and Answers Forum
Question Number 62145 by maxmathsup by imad last updated on 16/Jun/19
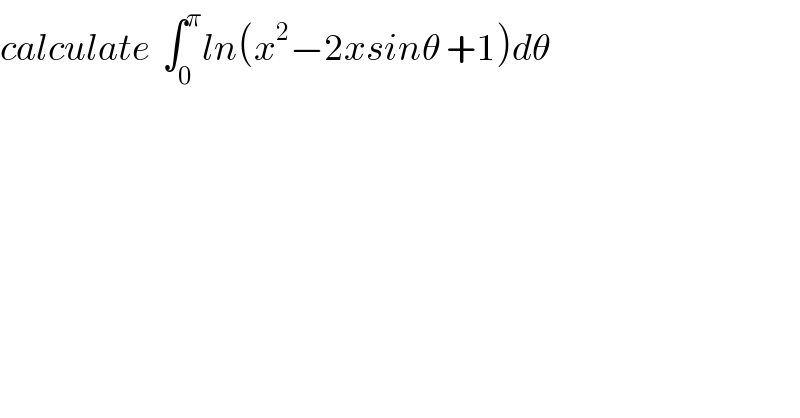
Commented by maxmathsup by imad last updated on 17/Jun/19

Answered by perlman last updated on 16/Jun/19
![let A(θ)=∫_0 ^π ln(x^2 −2xcos(θ)+1)dθ θ∈IR\{2kπ,k∈IZ} A(θ)=[xln(x^2 −2cos(θ)x+1)]_0 ^π −∫((2x^2 −2xcos(θ))/(x^2 −2cos(θ)x+1))dx =πln(π^2 −2cos(θ)π+1)−2∫_0 ^π ((x^2 −xcos(θ))/(x^2 −2cos(θ)x+1))dx ((x^2 −xcos(θ))/(x^2 −2cos(θ)x+1))=1+((xcos(θ)−1)/(x^2 −2cos(θ)x+1)) A(θ)=πln(π^2 −2cos(θ)π+1)−2∫_0 ^π 1+((xcos(θ)−1)/(x^2 −2cos(θ)x+1))dx the 2 nd integral =−2π −2∫_0 ^π ((xcos(θ)−1)/(x^2 −2cos(θ)x+1))dx=−2π−∫_0 ^π ((cos(θ)[2x−2cos(θ)]−2+2cos^2 (θ))/(x^2 −2cos(θ)x+1))dx =−2π−cos(θ)∫_0 ^π ((2x−2cos(θ))/(x^2 −2cos(θ)x+1))dx+2∫((sin^2 (θ))/(x^2 −2cos(θ)x+1))dx =−2π−cos(θ)[ln[x^2 −2cos(θ)x+1⌉_0 ^π +2sin^2 θ∫_0 ^π (1/((x−cos(θ))^2 +sin^2 (θ)))dx =2π−cos(θ)ln(π2−2cos(θ)π+1)+2∫_0 ^π (1/(((x/(sin(θ)))−cot (θ))^2 +1))dx if sin≠0 =−2π−cos(θ)ln(π^2 −2cos(θ)π+1)+2sin(θ){tan^(−1) {(x/(sinθ))−cot (θ)}_0 ^π } =−2π−cos(θ)ln{π^2 −2cos(θ)π+1}+2sin(θ){tan^(−1) {(π/(sin(θ)))−cot (θ)}−tan^(−1) {cot (−θ)} =−2π−cos(θ)ln{π^2 −2cos(θ)π+1}+2sin(θ){arctan{(π/(sin(θ)))−cot(θ)}−arctan(tg((π/2)+θ)) A(θ)=−2π+(π−cos(θ))ln(π^2 −2cos(θ)x+1)+2sin(θ)arctan(((π−cos(θ))/(sin(θ))))−2sin(θ)arctan(tan((π/2)+θ)) arctan(tg(a))=a if a∈]((−π)/2).(π/2)[ if a∈]−(π/2)+kπ.(π/2)+kπ[ arctantg(a)=a−kπ](Q62163.png)
| ||
Question and Answers Forum | ||
Question Number 62145 by maxmathsup by imad last updated on 16/Jun/19 | ||
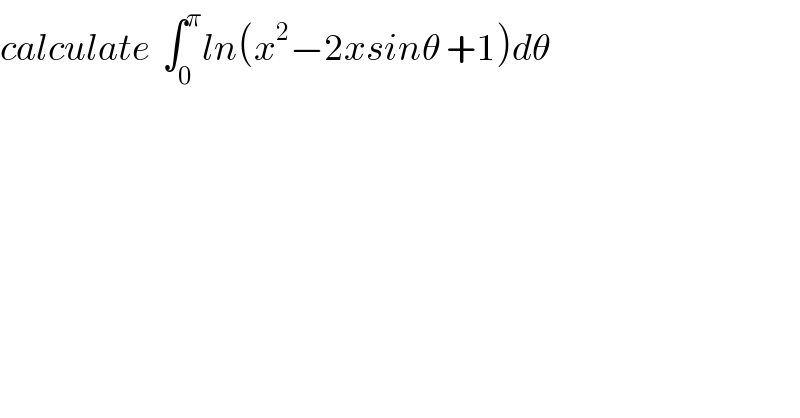 | ||
Commented by maxmathsup by imad last updated on 17/Jun/19 | ||
 | ||
Answered by perlman last updated on 16/Jun/19 | ||
![let A(θ)=∫_0 ^π ln(x^2 −2xcos(θ)+1)dθ θ∈IR\{2kπ,k∈IZ} A(θ)=[xln(x^2 −2cos(θ)x+1)]_0 ^π −∫((2x^2 −2xcos(θ))/(x^2 −2cos(θ)x+1))dx =πln(π^2 −2cos(θ)π+1)−2∫_0 ^π ((x^2 −xcos(θ))/(x^2 −2cos(θ)x+1))dx ((x^2 −xcos(θ))/(x^2 −2cos(θ)x+1))=1+((xcos(θ)−1)/(x^2 −2cos(θ)x+1)) A(θ)=πln(π^2 −2cos(θ)π+1)−2∫_0 ^π 1+((xcos(θ)−1)/(x^2 −2cos(θ)x+1))dx the 2 nd integral =−2π −2∫_0 ^π ((xcos(θ)−1)/(x^2 −2cos(θ)x+1))dx=−2π−∫_0 ^π ((cos(θ)[2x−2cos(θ)]−2+2cos^2 (θ))/(x^2 −2cos(θ)x+1))dx =−2π−cos(θ)∫_0 ^π ((2x−2cos(θ))/(x^2 −2cos(θ)x+1))dx+2∫((sin^2 (θ))/(x^2 −2cos(θ)x+1))dx =−2π−cos(θ)[ln[x^2 −2cos(θ)x+1⌉_0 ^π +2sin^2 θ∫_0 ^π (1/((x−cos(θ))^2 +sin^2 (θ)))dx =2π−cos(θ)ln(π2−2cos(θ)π+1)+2∫_0 ^π (1/(((x/(sin(θ)))−cot (θ))^2 +1))dx if sin≠0 =−2π−cos(θ)ln(π^2 −2cos(θ)π+1)+2sin(θ){tan^(−1) {(x/(sinθ))−cot (θ)}_0 ^π } =−2π−cos(θ)ln{π^2 −2cos(θ)π+1}+2sin(θ){tan^(−1) {(π/(sin(θ)))−cot (θ)}−tan^(−1) {cot (−θ)} =−2π−cos(θ)ln{π^2 −2cos(θ)π+1}+2sin(θ){arctan{(π/(sin(θ)))−cot(θ)}−arctan(tg((π/2)+θ)) A(θ)=−2π+(π−cos(θ))ln(π^2 −2cos(θ)x+1)+2sin(θ)arctan(((π−cos(θ))/(sin(θ))))−2sin(θ)arctan(tan((π/2)+θ)) arctan(tg(a))=a if a∈]((−π)/2).(π/2)[ if a∈]−(π/2)+kπ.(π/2)+kπ[ arctantg(a)=a−kπ](Q62163.png) | ||
| ||