
Question and Answers Forum
Question Number 62209 by maxmathsup by imad last updated on 17/Jun/19
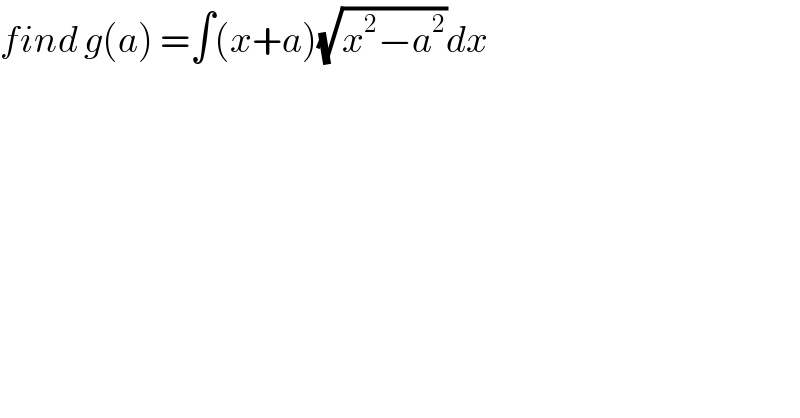
Commented by maxmathsup by imad last updated on 18/Jun/19

Answered by tanmay last updated on 17/Jun/19
![∫x(√(x^2 −a^2 )) dx+a∫(√(x^2 −a^2 )) dx (1/2)∫(x^2 −a^2 )^(1/2) d(x^2 −a^2 )+a∫(√(x^2 −a^2 )) dx (1/2)×(((x^2 −a^2 )^(3/2) )/(3/2))+a[((x(√(x^2 −a^2 )))/2)−(a^2 /2)ln(x+(√(x^2 −a^2 )) )]+c](Q62222.png)
| ||
Question and Answers Forum | ||
Question Number 62209 by maxmathsup by imad last updated on 17/Jun/19 | ||
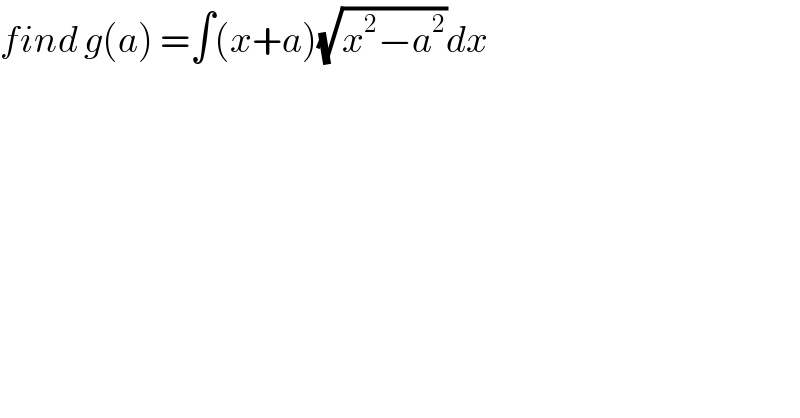 | ||
Commented by maxmathsup by imad last updated on 18/Jun/19 | ||
 | ||
Answered by tanmay last updated on 17/Jun/19 | ||
![∫x(√(x^2 −a^2 )) dx+a∫(√(x^2 −a^2 )) dx (1/2)∫(x^2 −a^2 )^(1/2) d(x^2 −a^2 )+a∫(√(x^2 −a^2 )) dx (1/2)×(((x^2 −a^2 )^(3/2) )/(3/2))+a[((x(√(x^2 −a^2 )))/2)−(a^2 /2)ln(x+(√(x^2 −a^2 )) )]+c](Q62222.png) | ||
| ||