
Question and Answers Forum
Question Number 62213 by maxmathsup by imad last updated on 17/Jun/19
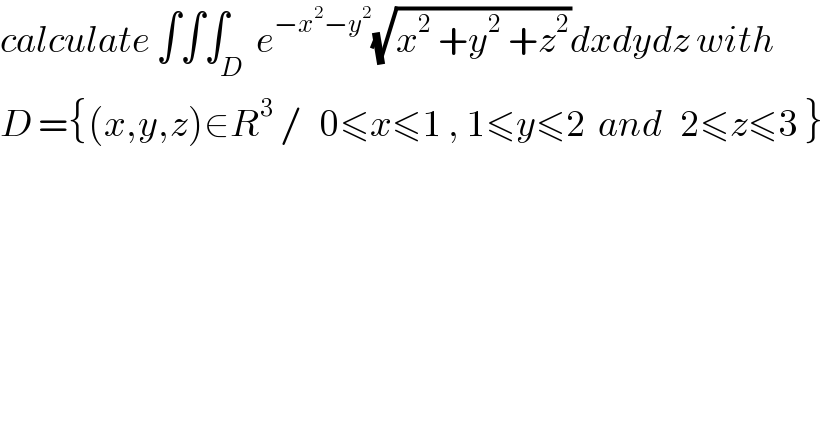
Commented by prof Abdo imad last updated on 20/Jun/19
![let use the diffeomorphism x=rcosθ ,y=rsinθ 0≤x≤1 and 1≤y≤2 ⇒1 ≤x^2 +y^2 ≤5 ⇒1≤r≤(√5) ∫∫∫_D e^(−x^2 −y^2 ) (√(x^2 +y^2 +z^2 ))dxdydz =∫_2 ^3 ( ∫_1 ^(√5) (e^(−r^2 ) (√(r^2 +z^2 )))rdr∫_0 ^(π/2) dθ)dz =(π/2) ∫_2 ^3 ( ∫_1 ^(√5) (re^(−r^2 ) (√(r^2 +z^2 ))dr)dz but by parts ∫_1 ^(√5) (re^(−r^2 ) )(√(r^2 +z^2 ))dr =[−(1/2) e^(−r^2 ) (√(r^2 +z^2 ))]_1 ^(√5) +(1/2)∫_1 ^(√5) e^(−r^2 ) ((2r)/(√(r^2 +z^2 ))) dr =(1/2)(e^(−1) (√(1+z^2 ))−e^(−5) (√(5+z^2 ))) +∫_1 ^(√5) ((re^(−r^2 ) )/(√(r^2 +z^2 ))) dr r =zu ⇒ ∫_1 ^(√5) ((r e^(−r^2 ) )/(√(r^2 +z^2 ))) dr =∫_(1/z) ^((√5)/z) ((zu e^(−z^2 u^2 ) )/(z(√(1+u^2 )))) zdu =z ∫_(1/z) ^((√5)/z) ((u e^(−z^2 u^2 ) )/(√(1+u^2 ))) du .....be continued...](Q62385.png)
| ||
Question and Answers Forum | ||
Question Number 62213 by maxmathsup by imad last updated on 17/Jun/19 | ||
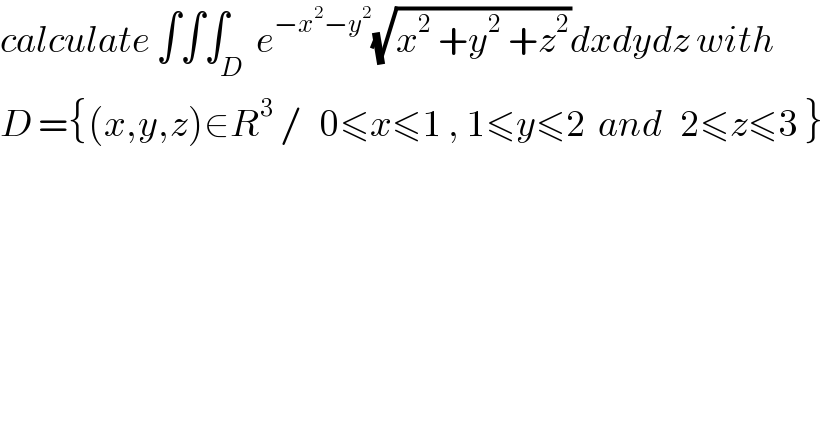 | ||
Commented by prof Abdo imad last updated on 20/Jun/19 | ||
![let use the diffeomorphism x=rcosθ ,y=rsinθ 0≤x≤1 and 1≤y≤2 ⇒1 ≤x^2 +y^2 ≤5 ⇒1≤r≤(√5) ∫∫∫_D e^(−x^2 −y^2 ) (√(x^2 +y^2 +z^2 ))dxdydz =∫_2 ^3 ( ∫_1 ^(√5) (e^(−r^2 ) (√(r^2 +z^2 )))rdr∫_0 ^(π/2) dθ)dz =(π/2) ∫_2 ^3 ( ∫_1 ^(√5) (re^(−r^2 ) (√(r^2 +z^2 ))dr)dz but by parts ∫_1 ^(√5) (re^(−r^2 ) )(√(r^2 +z^2 ))dr =[−(1/2) e^(−r^2 ) (√(r^2 +z^2 ))]_1 ^(√5) +(1/2)∫_1 ^(√5) e^(−r^2 ) ((2r)/(√(r^2 +z^2 ))) dr =(1/2)(e^(−1) (√(1+z^2 ))−e^(−5) (√(5+z^2 ))) +∫_1 ^(√5) ((re^(−r^2 ) )/(√(r^2 +z^2 ))) dr r =zu ⇒ ∫_1 ^(√5) ((r e^(−r^2 ) )/(√(r^2 +z^2 ))) dr =∫_(1/z) ^((√5)/z) ((zu e^(−z^2 u^2 ) )/(z(√(1+u^2 )))) zdu =z ∫_(1/z) ^((√5)/z) ((u e^(−z^2 u^2 ) )/(√(1+u^2 ))) du .....be continued...](Q62385.png) | ||