
Question and Answers Forum
Question Number 62252 by hovea cw last updated on 18/Jun/19
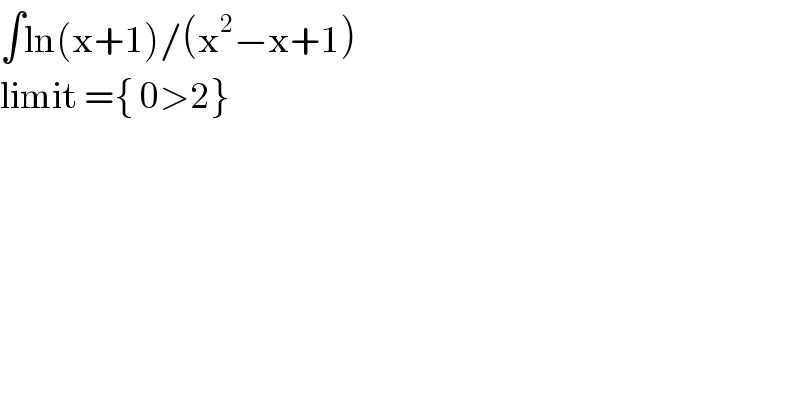
Commented bymaxmathsup by imad last updated on 18/Jun/19
![let I =∫_0 ^2 ((ln(x+1))/(x^2 −x +1))dx and f(t)=∫_0 ^2 ((ln(1+tx))/(x^2 −x +1)) dx with t≥0 we have I =f(1) and f^′ (t)=∫_0 ^2 (x/((1+tx)(x^2 −x+1)))dx =(1/t)∫_0 ^2 ((1+tx−1)/((1+tx)(x^2 −x+1)))dx =(1/t)∫_0 ^2 (dx/((x^2 −x+1))) −(1/t) ∫_0 ^2 (dx/((tx+1)(x^2 −x+1))) ∫_0 ^2 (dx/(x^2 −x+1)) =∫_0 ^2 (dx/((x−(1/2))^2 +(3/4))) =_(x−(1/2)=((√3)/2)u) (4/3) ∫_(−(1/(√3))) ^(3/(√3)) (1/(u^2 +1)) ((√3)/2)du =(2/(√3)) [arctn(u)]_(−(1/(√3))) ^(√3) =(2/(√3)){ arctan((√3))+arctan((1/(√3)))}=(2/(√3))(π/2) =(π/(√3)) let decompose F(x)=(1/((tx+1)(x^2 −x +1)→(Δ<0))) F(x) =(a/(tx+1)) +((bx+c)/(x^2 −x+1)) a =lim_(x→−(1/t)) (tx+1)F(x) =(t^2 /(t^2 +t+1)) ⇒F(x) =(t^2 /((tx+1)(t^2 +t+1))) +((bx+c)/(x^2 −x +1)) lim_(t→+∞) xF(x) =0 =(a/t) +b ⇒a+tb =0 ⇒tb =−a ⇒b =−(a/t) =−(t/(t^2 +t+1)) ⇒ F(x) =(t^2 /((t^2 +t+1)(tx+1))) +((−(t/(t^2 +t+1))x +c)/(x^2 −x+1)) F(0)=1 =a+c ⇒c =1−a =1−(t^2 /(t^2 +t+1)) =((t+1)/(t^2 +t+1)) ⇒ F(x) =(t^2 /((t^2 +t+1)(tx+1))) −(1/(t^2 +t+1)) ((tx−t−1)/(x^2 −x+1)) ⇒ ∫_0 ^2 F(x)dx =(t^2 /(t^2 +t+1)) ∫_0 ^2 (dx/(tx+1)) −(1/(t^2 +t+1)) ∫_0 ^2 ((tx−t−1)/(x^2 −x +1))dx ∫_0 ^2 (dx/(tx +1)) =(1/t)[ln∣tx+1∣]_0 ^2 =(1/t)ln∣2t+1∣ ∫_0 ^2 ((tx−t−1)/(x^2 −x+1))dx =(t/2)∫_0 ^2 ((2x−1+1)/(x^2 −x+1))dx −(t+1)∫_0 ^2 (dx/(x^2 −x+1)) =(t/2)[ln∣x^2 −x+1∣]_0 ^2 −(t+1)(π/(√3)) =(t/2)ln(3)−(π/(√3))(t+1) ⇒ ∫_0 ^2 F(x)dx =(t/(t^2 +t +1))ln∣2t+1∣ −(1/(t^2 +t+1)){(((ln(3))/2)−(π/(√3)))t−(π/(√3))} ⇒ f^′ (t) =(π/(t(√3))) −(1/t)∫_0 ^2 F(x)dx =(π/(t(√3))) −((ln∣2t+1∣)/(t^(2 ) +t +1)) −((((ln(3))/2)−(π/(√3)))/(t^2 +t +1)) +(π/(t(√3)(t^2 +t +1))) ⇒ f(t) =(π/(√3))ln(t)−∫ ((ln(2t+1))/(t^2 +t +1))dt −(((ln3)/2)−(π/(√3)))∫ (dt/(t^2 +t +1)) +(π/(√3)) ∫ (dt/(t(t^2 +t +1))) +c ...be continued...](Q62260.png)
| ||
Question and Answers Forum | ||
Question Number 62252 by hovea cw last updated on 18/Jun/19 | ||
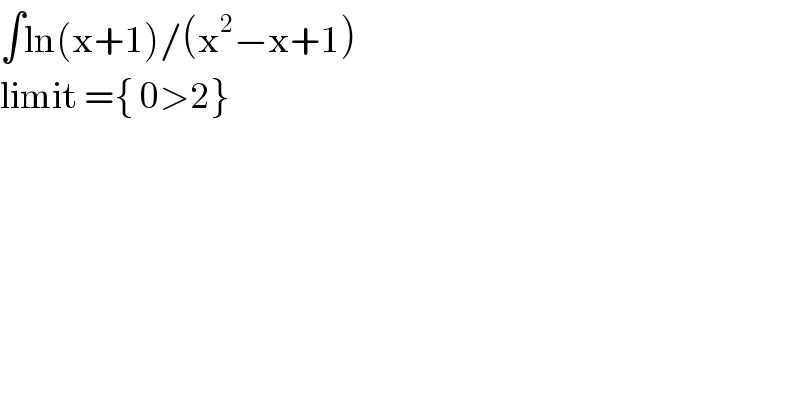 | ||
Commented bymaxmathsup by imad last updated on 18/Jun/19 | ||
![let I =∫_0 ^2 ((ln(x+1))/(x^2 −x +1))dx and f(t)=∫_0 ^2 ((ln(1+tx))/(x^2 −x +1)) dx with t≥0 we have I =f(1) and f^′ (t)=∫_0 ^2 (x/((1+tx)(x^2 −x+1)))dx =(1/t)∫_0 ^2 ((1+tx−1)/((1+tx)(x^2 −x+1)))dx =(1/t)∫_0 ^2 (dx/((x^2 −x+1))) −(1/t) ∫_0 ^2 (dx/((tx+1)(x^2 −x+1))) ∫_0 ^2 (dx/(x^2 −x+1)) =∫_0 ^2 (dx/((x−(1/2))^2 +(3/4))) =_(x−(1/2)=((√3)/2)u) (4/3) ∫_(−(1/(√3))) ^(3/(√3)) (1/(u^2 +1)) ((√3)/2)du =(2/(√3)) [arctn(u)]_(−(1/(√3))) ^(√3) =(2/(√3)){ arctan((√3))+arctan((1/(√3)))}=(2/(√3))(π/2) =(π/(√3)) let decompose F(x)=(1/((tx+1)(x^2 −x +1)→(Δ<0))) F(x) =(a/(tx+1)) +((bx+c)/(x^2 −x+1)) a =lim_(x→−(1/t)) (tx+1)F(x) =(t^2 /(t^2 +t+1)) ⇒F(x) =(t^2 /((tx+1)(t^2 +t+1))) +((bx+c)/(x^2 −x +1)) lim_(t→+∞) xF(x) =0 =(a/t) +b ⇒a+tb =0 ⇒tb =−a ⇒b =−(a/t) =−(t/(t^2 +t+1)) ⇒ F(x) =(t^2 /((t^2 +t+1)(tx+1))) +((−(t/(t^2 +t+1))x +c)/(x^2 −x+1)) F(0)=1 =a+c ⇒c =1−a =1−(t^2 /(t^2 +t+1)) =((t+1)/(t^2 +t+1)) ⇒ F(x) =(t^2 /((t^2 +t+1)(tx+1))) −(1/(t^2 +t+1)) ((tx−t−1)/(x^2 −x+1)) ⇒ ∫_0 ^2 F(x)dx =(t^2 /(t^2 +t+1)) ∫_0 ^2 (dx/(tx+1)) −(1/(t^2 +t+1)) ∫_0 ^2 ((tx−t−1)/(x^2 −x +1))dx ∫_0 ^2 (dx/(tx +1)) =(1/t)[ln∣tx+1∣]_0 ^2 =(1/t)ln∣2t+1∣ ∫_0 ^2 ((tx−t−1)/(x^2 −x+1))dx =(t/2)∫_0 ^2 ((2x−1+1)/(x^2 −x+1))dx −(t+1)∫_0 ^2 (dx/(x^2 −x+1)) =(t/2)[ln∣x^2 −x+1∣]_0 ^2 −(t+1)(π/(√3)) =(t/2)ln(3)−(π/(√3))(t+1) ⇒ ∫_0 ^2 F(x)dx =(t/(t^2 +t +1))ln∣2t+1∣ −(1/(t^2 +t+1)){(((ln(3))/2)−(π/(√3)))t−(π/(√3))} ⇒ f^′ (t) =(π/(t(√3))) −(1/t)∫_0 ^2 F(x)dx =(π/(t(√3))) −((ln∣2t+1∣)/(t^(2 ) +t +1)) −((((ln(3))/2)−(π/(√3)))/(t^2 +t +1)) +(π/(t(√3)(t^2 +t +1))) ⇒ f(t) =(π/(√3))ln(t)−∫ ((ln(2t+1))/(t^2 +t +1))dt −(((ln3)/2)−(π/(√3)))∫ (dt/(t^2 +t +1)) +(π/(√3)) ∫ (dt/(t(t^2 +t +1))) +c ...be continued...](Q62260.png) | ||