
Question and Answers Forum
Question Number 62332 by tanmay last updated on 19/Jun/19
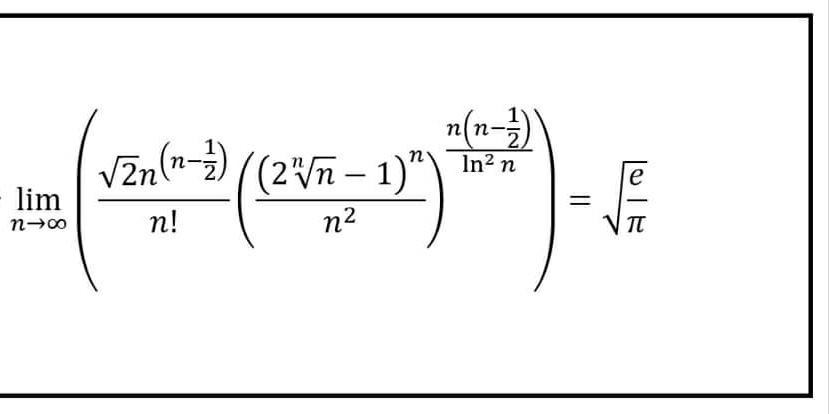
Answered by tanmay last updated on 20/Jun/19
![lim_(n→∞) [(((√2) ×n^(n−(1/2)) )/(n^(n+(1/2)) ×(√(2π)) ×e^(−n) ))×{(((2×n^(1/n) −1)^n )/n^2 )}^((n(n−(1/2)))/(ln^2 n)) ] =(1/(√π))lim_(n→∞) [(e^n /n)×{(((2×n^(1/n) −1)^n )/n^2 )}^((n(n−(1/2)))/(ln^2 n)) ] now =(1/(√π))lim_(n→∞) [(e^n /n)×{(((2n^(1/n) −1)^n^2 )/n^(2n) )}^((n−(1/2))/(ln^2 n)) ] =(1/(√π))lim_(n→∞) [(e^n /n)×{((n^n (2−(1/n^(1/n) ))^n^2 )/(n^n ×n^n ))}^((n−(1/2))/(ln^2 n)) ] =(1/(√π))lim_(n→∞) [(e^n /n)×{((2^n^2 (1−(1/(2n^(1/n) )))^n^2 )/n^n )}^((n−(1/2))/(ln^2 n)) ] =(1/(√π))lim_(n→∞) [(e^n /n)×{(2^n^2 /n^n )×(1−(1/(2n^(1/n) )))^(2n^(1/n) ×(n^2 /(2n^(1/n) ))) }^((n−(1/2))/(ln^2 n)) ] =(1/(√π))lim_(n→∞) [(e^n /n)×{(2^n^2 /n^n )×e^(−(n^2 /(2n^(1/n) ))) }^((n−(1/2))/(ln^2 n)) ] =(1/(√π))lim_(n→∞) [(e^n /n)×2^(n^2 ×((n−(1/2))/(ln^2 n))) ×(1/n^((n−(1/2))/(ln^2 n)) )×(e^((−1)/2) )^((n^2 /n^(1/n) )×((n−(1/2))/(ln^2 n))) ] (1/(√π))lim_(n→∞) wait](Q62359.png)
| ||
Question and Answers Forum | ||
Question Number 62332 by tanmay last updated on 19/Jun/19 | ||
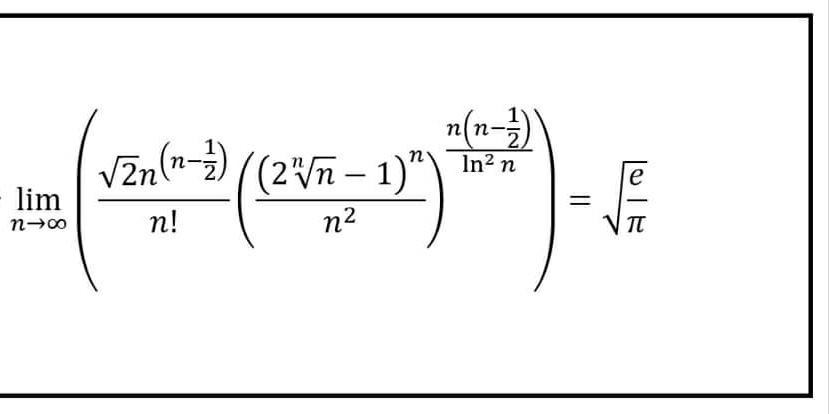 | ||
Answered by tanmay last updated on 20/Jun/19 | ||
![lim_(n→∞) [(((√2) ×n^(n−(1/2)) )/(n^(n+(1/2)) ×(√(2π)) ×e^(−n) ))×{(((2×n^(1/n) −1)^n )/n^2 )}^((n(n−(1/2)))/(ln^2 n)) ] =(1/(√π))lim_(n→∞) [(e^n /n)×{(((2×n^(1/n) −1)^n )/n^2 )}^((n(n−(1/2)))/(ln^2 n)) ] now =(1/(√π))lim_(n→∞) [(e^n /n)×{(((2n^(1/n) −1)^n^2 )/n^(2n) )}^((n−(1/2))/(ln^2 n)) ] =(1/(√π))lim_(n→∞) [(e^n /n)×{((n^n (2−(1/n^(1/n) ))^n^2 )/(n^n ×n^n ))}^((n−(1/2))/(ln^2 n)) ] =(1/(√π))lim_(n→∞) [(e^n /n)×{((2^n^2 (1−(1/(2n^(1/n) )))^n^2 )/n^n )}^((n−(1/2))/(ln^2 n)) ] =(1/(√π))lim_(n→∞) [(e^n /n)×{(2^n^2 /n^n )×(1−(1/(2n^(1/n) )))^(2n^(1/n) ×(n^2 /(2n^(1/n) ))) }^((n−(1/2))/(ln^2 n)) ] =(1/(√π))lim_(n→∞) [(e^n /n)×{(2^n^2 /n^n )×e^(−(n^2 /(2n^(1/n) ))) }^((n−(1/2))/(ln^2 n)) ] =(1/(√π))lim_(n→∞) [(e^n /n)×2^(n^2 ×((n−(1/2))/(ln^2 n))) ×(1/n^((n−(1/2))/(ln^2 n)) )×(e^((−1)/2) )^((n^2 /n^(1/n) )×((n−(1/2))/(ln^2 n))) ] (1/(√π))lim_(n→∞) wait](Q62359.png) | ||
| ||