let f(ξ) =∫ (x^2 /(√(1−ξx^2 )))dx with 0<ξ<1 1) determine a explicit form of f(ξ) 2) calculate lim_(ξ→1) f(ξ) 3) calculate ∫_0 ^(1/2) (x^2 /(√(1−sin^2 θ x^2 ))) dx with 0<θ<(π/2)


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 62342 by maxmathsup by imad last updated on 20/Jun/19

$l e t f (ξ) = \int \frac{x^{2}}{\sqrt{1 - ξ x^{2}}} d x w i t h 0 < ξ < 1$ $1) d e t e r m i n e a e x p l i c i t f o r m o f f (ξ)$ $2) c a l c u l a t e {l i m}_{ξ \to 1} f (ξ)$ $3) c a l c u l a t e \int_{0}^{\frac{1}{2}} \frac{x^{2}}{\sqrt{1 - {s i n}^{2} θ x^{2}}} d x w i t h 0 < θ < \frac{π}{2}$
Commented byprof Abdo imad last updated on 20/Jun/19
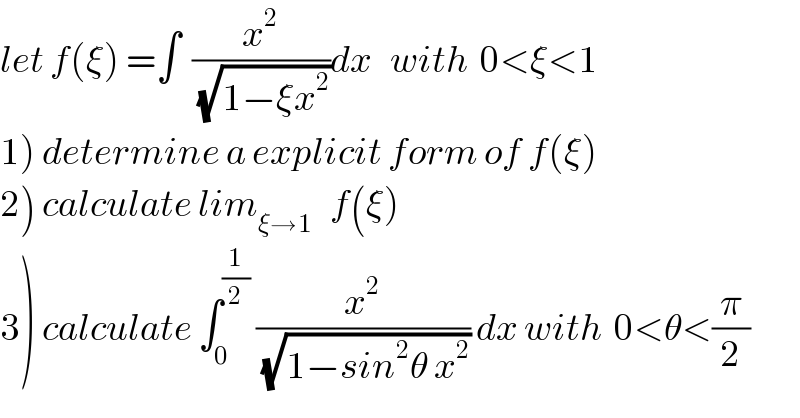
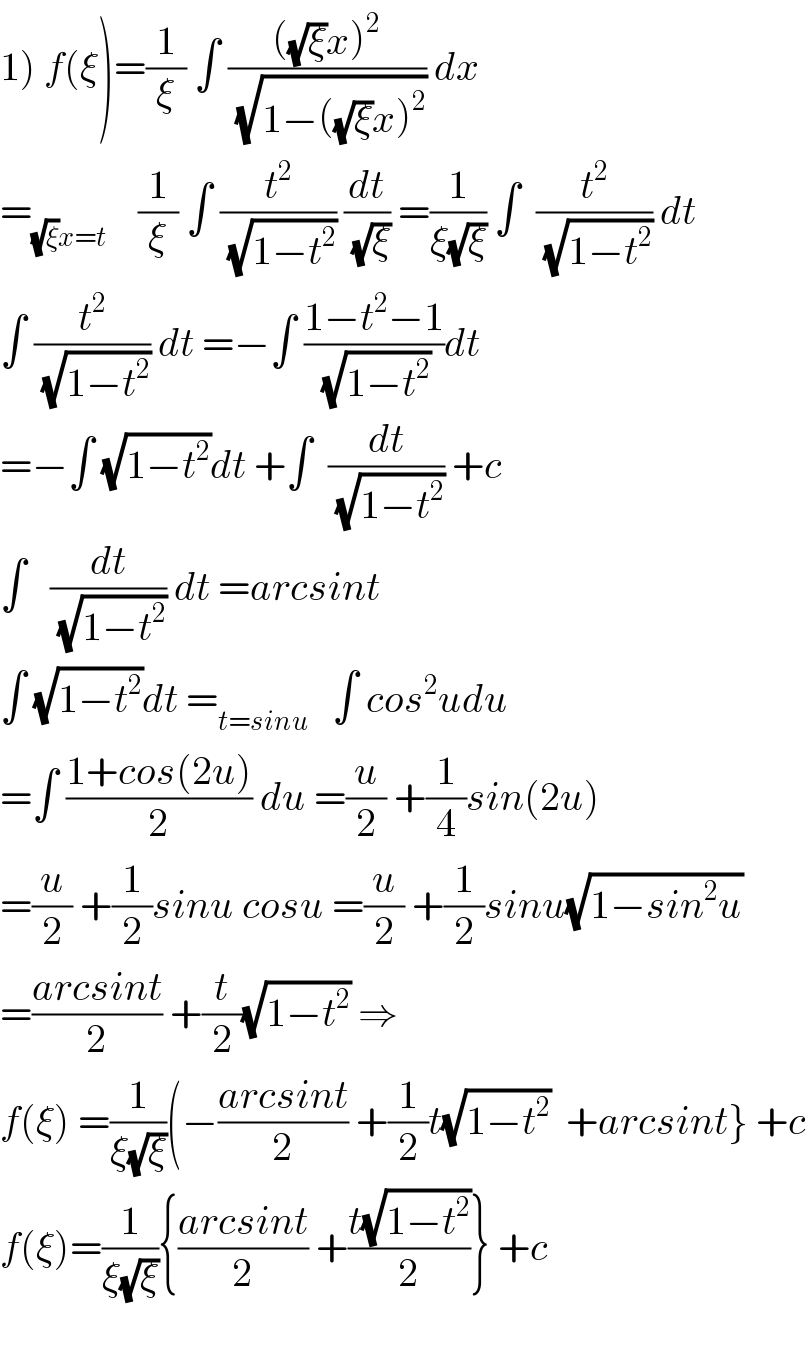
$1) f(ξ)=(1/ξ) ∫ ((((√ξ)x)^2 )/(√(1−((√ξ)x)^2 ))) dx =_((√ξ)x=t) (1/ξ) ∫ (t^2 /(√(1−t^2 ))) (dt/(√ξ)) =(1/(ξ(√ξ))) ∫ (t^2 /(√(1−t^2 ))) dt ∫ (t^2 /(√(1−t^2 ))) dt =−∫ ((1−t^2 −1)/(√(1−t^2 )))dt =−∫ (√(1−t^2 ))dt +∫ (dt/(√(1−t^2 ))) +c ∫ (dt/(√(1−t^2 ))) dt =arcsint ∫ (√(1−t^2 ))dt =_(t=sinu) ∫ cos^2 udu =∫ ((1+cos(2u))/2) du =(u/2) +(1/4)sin(2u) =(u/2) +(1/2)sinu cosu =(u/2) +(1/2)sinu(√(1−sin^2 u)) =((arcsint)/2) +(t/2)(√(1−t^2 )) ⇒ f(ξ) =(1/(ξ(√ξ)))(−((arcsint)/2) +(1/2)t(√(1−t^2 )) +arcsint} +c f(ξ)=(1/(ξ(√ξ))){((arcsint)/2) +((t(√(1−t^2 )))/2)} +c$
$1) f (ξ) = \frac{1}{ξ} \int \frac{{(\sqrt{ξ} x)}^{2}}{\sqrt{1 - {(\sqrt{ξ} x)}^{2}}} d x$ $=_{\sqrt{ξ} x = t} \frac{1}{ξ} \int \frac{t^{2}}{\sqrt{1 - t^{2}}} \frac{d t}{\sqrt{ξ}} = \frac{1}{ξ \sqrt{ξ}} \int \frac{t^{2}}{\sqrt{1 - t^{2}}} d t$ $\int \frac{t^{2}}{\sqrt{1 - t^{2}}} d t = - \int \frac{1 - t^{2} - 1}{\sqrt{1 - t^{2}}} d t$ $= - \int \sqrt{1 - t^{2}} d t + \int \frac{d t}{\sqrt{1 - t^{2}}} + c$ $\int \frac{d t}{\sqrt{1 - t^{2}}} d t = a r c s i n t$ $\int \sqrt{1 - t^{2}} d t =_{t = s i n u} \int {c o s}^{2} u d u$ $= \int \frac{1 + c o s (2 u)}{2} d u = \frac{u}{2} + \frac{1}{4} s i n (2 u)$ $= \frac{u}{2} + \frac{1}{2} s i n u c o s u = \frac{u}{2} + \frac{1}{2} s i n u \sqrt{1 - {s i n}^{2} u}$ $= \frac{a r c s i n t}{2} + \frac{t}{2} \sqrt{1 - t^{2}} \Rightarrow$ $f (ξ) = \frac{1}{ξ \sqrt{ξ}} (- \frac{a r c s i n t}{2} + \frac{1}{2} t \sqrt{1 - t^{2}} + a r c s i n t} + c$ $f (ξ) = \frac{1}{ξ \sqrt{ξ}} {\frac{a r c s i n t}{2} + \frac{t \sqrt{1 - t^{2}}}{2}} + c$
Commented byprof Abdo imad last updated on 20/Jun/19
$t =x(√ξ) ⇒ f(ξ) =(1/(2ξ(√ξ))){ arcsin(x(√ξ))+x(√ξ)(√(1−ξx^2 ))} +c$
$t = x \sqrt{ξ} \Rightarrow$ $f (ξ) = \frac{1}{2 ξ \sqrt{ξ}} {a r c s i n (x \sqrt{ξ}) + x \sqrt{ξ} \sqrt{1 - ξ x^{2}}} + c$
Commented byprof Abdo imad last updated on 20/Jun/19

$2) {l i m}_{ξ \to 1} f (ξ) = \frac{1}{2} (a r c s i n (x) + x \sqrt{1 - x^{2}}) + c$
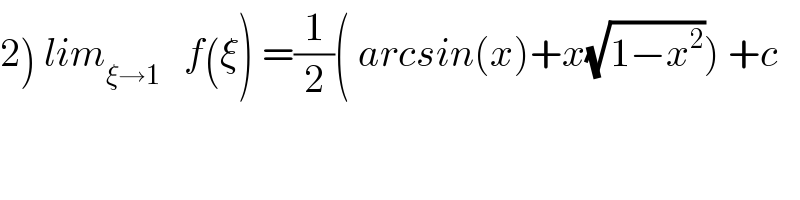
Commented byprof Abdo imad last updated on 20/Jun/19
$3) ∫_0 ^(1/2) (x^2 /(√(1−sin^2 θ x^2 )))dx (ξ=sin^2 θ) =[(1/(2sin^3 θ)){arcsin(xsinθ) +xsinθ(√(1−sin^2 θ x^2 ))}]_0 ^(1/2) =(1/(2sin^3 θ)){ arcsin(((sinθ)/2))+(1/2)sinθ(√(1−(1/4)sin^2 θ))}$
$3) \int_{0}^{\frac{1}{2}} \frac{x^{2}}{\sqrt{1 - {s i n}^{2} θ x^{2}}} d x (ξ = {s i n}^{2} θ)$ $= {[\frac{1}{2 {s i n}^{3} θ} {a r c s i n (x s i n θ) + x s i n θ \sqrt{1 - {s i n}^{2} θ x^{2}}}]}_{0}^{\frac{1}{2}}$ $= \frac{1}{2 {s i n}^{3} θ} {a r c s i n (\frac{s i n θ}{2}) + \frac{1}{2} s i n θ \sqrt{1 - \frac{1}{4} {s i n}^{2} θ}}$
	Answered by mr W last updated on 20/Jun/19

	$f (ξ) = \int \frac{x^{2}}{\sqrt{1 - ξ x^{2}}} d x$ $= \frac{1}{ξ} \int \frac{{(\sqrt{ξ} x)}^{2}}{\sqrt{1 - {(\sqrt{ξ} x)}^{2}}} d (\sqrt{ξ} x)$ $= \frac{1}{ξ} \int \frac{t^{2}}{\sqrt{1 - t^{2}}} d t$ $= \frac{1}{ξ} \int [\frac{1}{\sqrt{1 - t^{2}}} - \sqrt{1 - t^{2}}] d t$ $= . . . .$ $= \frac{1}{2 ξ} [\frac{1}{\sqrt{ξ}} \sin^{- 1} (\sqrt{ξ} x) - x \sqrt{1 - ξ x^{2}}] + C$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum