
Question and Answers Forum
Question Number 62415 by mathmax by abdo last updated on 20/Jun/19
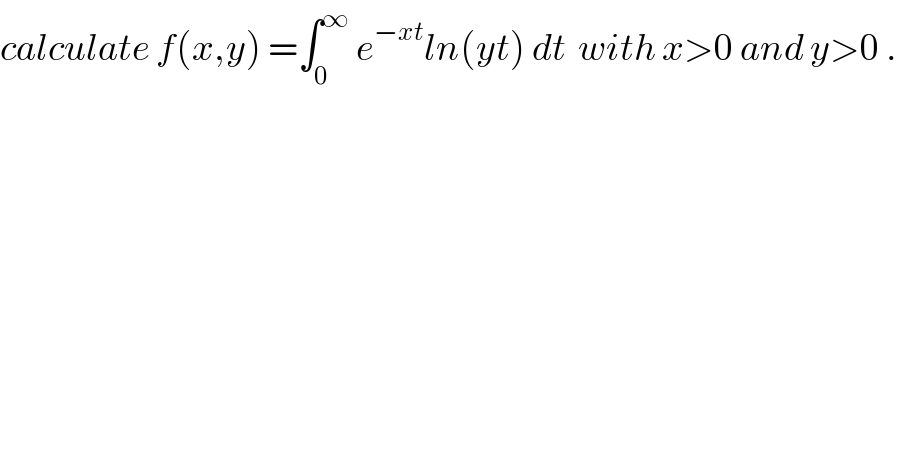
Commented bymathmax by abdo last updated on 23/Jun/19
![we have f(x,y) =∫_0 ^∞ e^(−xt) (lny +ln(t)dt =ln(y)∫_0 ^∞ e^(−xt) dt +∫_0 ^∞ e^(−xt) ln(t)dt ∫_0 ^∞ e^(−xt) dt =[−(1/x)e^(−xt) ]_(t=0) ^∞ =(1/x) ∫_0 ^∞ e^(−xt) ln(t) dt =_(xt =u) ∫_0 ^∞ e^(−u) ln((u/x))(du/x) =(1/x){ ∫_0 ^∞ e^(−u) ln(u)du−ln(x)∫_0 ^∞ e^(−u) du} =(1/x){ −γ −ln(x)×1} =−(1/x){ln(x)+γ) ⇒ f(x,y) =((ln(y))/x) −(1/x){ln(x)+γ} =(1/x)( ln((y/x))−γ) γ is euler constant number.](Q62567.png)
| ||
Question and Answers Forum | ||
Question Number 62415 by mathmax by abdo last updated on 20/Jun/19 | ||
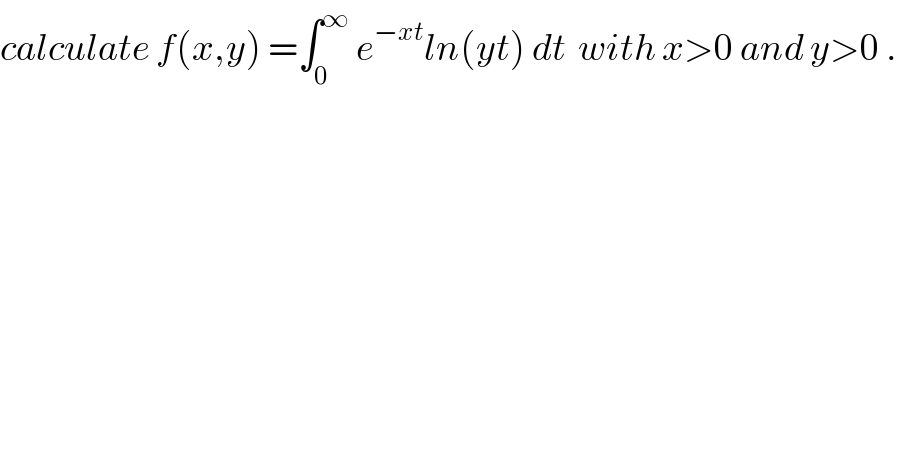 | ||
Commented bymathmax by abdo last updated on 23/Jun/19 | ||
![we have f(x,y) =∫_0 ^∞ e^(−xt) (lny +ln(t)dt =ln(y)∫_0 ^∞ e^(−xt) dt +∫_0 ^∞ e^(−xt) ln(t)dt ∫_0 ^∞ e^(−xt) dt =[−(1/x)e^(−xt) ]_(t=0) ^∞ =(1/x) ∫_0 ^∞ e^(−xt) ln(t) dt =_(xt =u) ∫_0 ^∞ e^(−u) ln((u/x))(du/x) =(1/x){ ∫_0 ^∞ e^(−u) ln(u)du−ln(x)∫_0 ^∞ e^(−u) du} =(1/x){ −γ −ln(x)×1} =−(1/x){ln(x)+γ) ⇒ f(x,y) =((ln(y))/x) −(1/x){ln(x)+γ} =(1/x)( ln((y/x))−γ) γ is euler constant number.](Q62567.png) | ||