
Question Number 6248 by FilupSmith last updated on 20/Jun/16

$$\int_{−\infty} ^{\:\infty} {e}^{−{u}} {u}^{{n}} {du}\:=\:??? \\ $$
Commented by 123456 last updated on 20/Jun/16
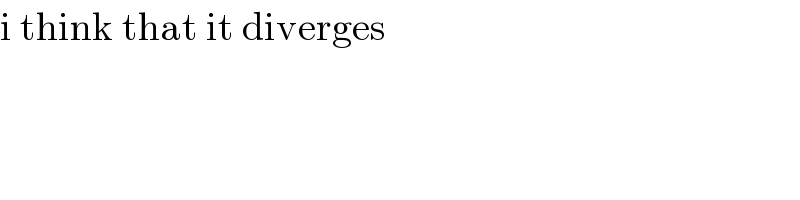
$$\mathrm{i}\:\mathrm{think}\:\mathrm{that}\:\mathrm{it}\:\mathrm{diverges} \\ $$
Commented by FilupSmith last updated on 21/Jun/16
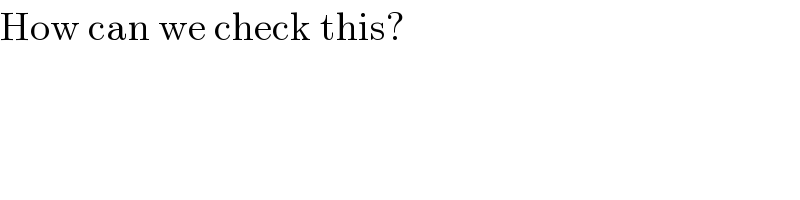
$$\mathrm{How}\:\mathrm{can}\:\mathrm{we}\:\mathrm{check}\:\mathrm{this}? \\ $$
Commented by nburiburu last updated on 24/Jun/16
![It can be solved by parts: ∫u.dv=u.v−∫v.du with u=x^n → du=n.x^(n−1) dv= e^(−x) dx→ v=−e^(−x) since u has a degree of n it needs to derivate n times. So, inductively: ∫e^(−x) x^n dx= −e^(−x) x^n −ne^(−x) x^(n−1) −n(n−1)e^(−x) x^(n−2) −...−((n!)/((n−i)!)) e^(−x) x^(n−i) −...−n! e^(−x) ∫e^(−x) x^n dx=−e^(−x) Σ_(i=0) ^n ((n!)/((n−i)!)) x^(n−i) Lastly ∫_(−∞) ^(+∞) e^(−x) x^n dx=(−e^(−x) Σ_(i=0) ^n ((n!)/((n−i)!))x^(n−i) )∣_(−∞) ^(+∞) = =−[ lim_(x→+∞) (Σ_(i=0) ^n ((n!)/((n−i)!)) x^(n−i) )/e^x −lim_(x→−∞) (Σ_(i=0) ^n ((n!)/((n−i)!)) x^(n−i) )/e^x ]= = 0 + ∞ = +∞ The first limit gives 0 because it is a polinomial divided exponential and using L′hospital theorem can be demonstrated. The last limit gives ∞/0 =+∞](Q6326.png)
$${It}\:{can}\:{be}\:{solved}\:{by}\:{parts}: \\ $$$$\int{u}.{dv}={u}.{v}−\int{v}.{du} \\ $$$${with} \\ $$$${u}={x}^{{n}} \:\rightarrow\:{du}={n}.{x}^{{n}−\mathrm{1}} \\ $$$${dv}=\:{e}^{−{x}} {dx}\rightarrow\:{v}=−{e}^{−{x}} \\ $$$${since}\:{u}\:{has}\:{a}\:{degree}\:{of}\:{n}\:{it}\:{needs}\:{to}\:{derivate}\:{n}\:{times}. \\ $$$${So},\:{inductively}: \\ $$$$\int{e}^{−{x}} {x}^{{n}} \:{dx}=\:−{e}^{−{x}} {x}^{{n}} −{ne}^{−{x}} {x}^{{n}−\mathrm{1}} −{n}\left({n}−\mathrm{1}\right){e}^{−{x}} {x}^{{n}−\mathrm{2}} −...−\frac{{n}!}{\left({n}−{i}\right)!}\:{e}^{−{x}} {x}^{{n}−{i}} −...−{n}!\:{e}^{−{x}} \\ $$$$\int{e}^{−{x}} {x}^{{n}} {dx}=−{e}^{−{x}} \:\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{n}!}{\left({n}−{i}\right)!}\:{x}^{{n}−{i}} \\ $$$${Lastly} \\ $$$$\int_{−\infty} ^{+\infty} {e}^{−{x}} \:{x}^{{n}} {dx}=\left(−{e}^{−{x}} \underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{n}!}{\left({n}−{i}\right)!}{x}^{{n}−{i}} \right)\mid_{−\infty} ^{+\infty} \:= \\ $$$$=−\left[\:\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\left(\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{n}!}{\left({n}−{i}\right)!}\:{x}^{{n}−{i}} \right)/{e}^{{x}} \:−\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left(\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{n}!}{\left({n}−{i}\right)!}\:{x}^{{n}−{i}} \right)/{e}^{{x}} \:\right]= \\ $$$$=\:\mathrm{0}\:+\:\infty\:=\:+\infty \\ $$$${The}\:{first}\:{limit}\:{gives}\:\mathrm{0}\:{because}\:{it}\:{is}\:{a}\:{polinomial}\:{divided}\:{exponential}\:{and}\:{using}\:{L}'{hospital}\:{theorem}\:{can}\:{be}\:{demonstrated}. \\ $$$${The}\:{last}\:{limit}\:{gives}\:\infty/\mathrm{0}\:=+\infty \\ $$$$ \\ $$$$ \\ $$
