Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 62542 by mr W last updated on 22/Jun/19

Commented by mr W last updated on 22/Jun/19

$t h e d i s t a n c e s o f a p o i n t M t o t h e$ $v e r t e x e s o f a t r i a n g l e a r e p, q, r .$ $f i n d t h e s i d e l e n g t h e s a n d h e n c e t h e$ $p e r i m e t e r o f t h e t r i a n g l e w i t h t h e$ $l a r g e s t p e r i m e t e r .$
	Answered by mr W last updated on 23/Jun/19
	$i think M should be center of incircle such that perimeter is maximum. let k=radius of incircle ∠A=2 sin^(−1) (k/p) ∠B=2 sin^(−1) (k/q) ∠C=2 sin^(−1) (k/r) ∠A+∠B+∠C=π ⇒sin^(−1) (k/p)+sin^(−1) (k/q)+sin^(−1) (k/r)=(π/2) ⇒cos (sin^(−1) (k/p)+sin^(−1) (k/q))=cos ((π/2)−sin^(−1) (k/r)) (√((1−(k^2 /p^2 ))(1−(k^2 /q^2 ))))−(k^2 /(pq))=(k/r) (√((1−(k^2 /p^2 ))(1−(k^2 /q^2 ))))=(k/r)+(k^2 /(pq)) (1−(k^2 /p^2 ))(1−(k^2 /q^2 ))=(k^2 /r^2 )+(k^4 /(p^2 q^2 ))+((2k^3 )/(pqr)) ((2k^3 )/(pqr))+((1/p^2 )+(1/q^2 )+(1/r^2 ))k^2 −1=0 k^3 +3((p^2 q^2 +q^2 r^2 +r^2 p^2 )/(6pqr))k^2 −2((pqr)/4)=0 ⇒k^3 +3uk^2 −2v=0 k=s−u ⇒s^3 −3u^2 s+2(u^3 −v)=0 s=2u sin {(1/3) sin^(−1) (1−(v/u^3 ))+((2nπ)/3)} k=u[2 sin {(1/3) sin^(−1) (1−(v/u^3 ))+((2π)/3)}−1]>0 ⇒k=((p^2 q^2 +q^2 r^2 +r^2 p^2 )/(6pqr))[2 sin {(1/3) sin^(−1) (1−((54p^4 q^4 r^4 )/((p^2 q^2 +q^2 r^2 +r^2 p^2 )^3 )))+((2π)/3)}−1] ⇒a=(√(q^2 −k^2 ))+(√(r^2 −k^2 )) ⇒b=(√(r^2 −k^2 ))+(√(p^2 −k^2 )) ⇒c=(√(p^2 −k^2 ))+(√(q^2 −k^2 ))$
	$i t h i n k M s h o u l d b e c e n t e r o f i n c i r c l e$ $s u c h t h a t p e r i m e t e r i s m a x i m u m .$ $l e t k = r a d i u s o f i n c i r c l e$ $∠ A = 2 \sin^{- 1} \frac{k}{p}$ $∠ B = 2 \sin^{- 1} \frac{k}{q}$ $∠ C = 2 \sin^{- 1} \frac{k}{r}$ $∠ A + ∠ B + ∠ C = π$ $\Rightarrow \sin^{- 1} \frac{k}{p} + \sin^{- 1} \frac{k}{q} + \sin^{- 1} \frac{k}{r} = \frac{π}{2}$ $\Rightarrow \cos (\sin^{- 1} \frac{k}{p} + \sin^{- 1} \frac{k}{q}) = \cos (\frac{π}{2} - \sin^{- 1} \frac{k}{r})$ $\sqrt{(1 - \frac{k^{2}}{p^{2}}) (1 - \frac{k^{2}}{q^{2}})} - \frac{k^{2}}{p q} = \frac{k}{r}$ $\sqrt{(1 - \frac{k^{2}}{p^{2}}) (1 - \frac{k^{2}}{q^{2}})} = \frac{k}{r} + \frac{k^{2}}{p q}$ $(1 - \frac{k^{2}}{p^{2}}) (1 - \frac{k^{2}}{q^{2}}) = \frac{k^{2}}{r^{2}} + \frac{k^{4}}{p^{2} q^{2}} + \frac{2 k^{3}}{p q r}$ $\frac{2 k^{3}}{p q r} + (\frac{1}{p^{2}} + \frac{1}{q^{2}} + \frac{1}{r^{2}}) k^{2} - 1 = 0$ $k^{3} + 3 \frac{p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2}}{6 p q r} k^{2} - 2 \frac{p q r}{4} = 0$ $\Rightarrow k^{3} + 3 {u k}^{2} - 2 v = 0$ $k = s - u$ $\Rightarrow s^{3} - 3 u^{2} s + 2 (u^{3} - v) = 0$ $s = 2 u \sin {\frac{1}{3} \sin^{- 1} (1 - \frac{v}{u^{3}}) + \frac{2 n π}{3}}$ $k = u [2 \sin {\frac{1}{3} \sin^{- 1} (1 - \frac{v}{u^{3}}) + \frac{2 π}{3}} - 1] > 0$ $\Rightarrow k = \frac{p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2}}{6 p q r} [2 \sin {\frac{1}{3} \sin^{- 1} (1 - \frac{54 p^{4} q^{4} r^{4}}{{(p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2})}^{3}}) + \frac{2 π}{3}} - 1]$ $\Rightarrow a = \sqrt{q^{2} - k^{2}} + \sqrt{r^{2} - k^{2}}$ $\Rightarrow b = \sqrt{r^{2} - k^{2}} + \sqrt{p^{2} - k^{2}}$ $\Rightarrow c = \sqrt{p^{2} - k^{2}} + \sqrt{q^{2} - k^{2}}$
	Commented by ajfour last updated on 22/Jun/19

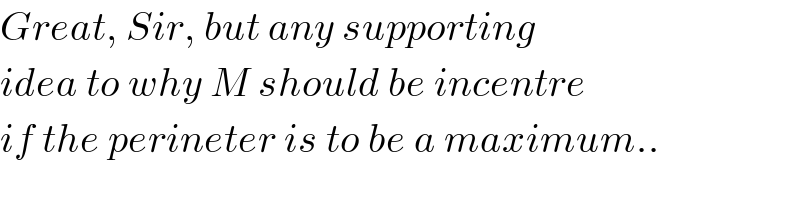
	$G r e a t, S i r, b u t a n y s u p p o r t i n g$ $i d e a t o w h y M s h o u l d b e i n c e n t r e$ $i f t h e p e r i n e t e r i s t o b e a m a x i m u m . .$
	Commented by mr W last updated on 23/Jun/19

	Commented by mr W last updated on 23/Jun/19

	$(s e e d i a g r a m a b o v e)$ ${l e t}^{'} s l o o k a t t h e c a s e w h e n B, C a r e$ $g i v e n a n d A i s t o d e t e r m i n e, w h i c h$ $m u s t l i e o n a c i r c l e w i t h c e n t e r M .$ $t h e l a w o f n a t u r e t e l l s u s : w h e n t h e$ $p a t h f r o m B t o C v i a A s h o u l d b e$ $o p t i m u m (m i n i m u m o r m a x i m u m),$ $i t m u s t f o l l o w t h e p a t h o f a l i g h t r a y,$ $i . e . a s i f t h e c i r c l e w e r e a m i r r o r .$ $p o i n t A s h o u l d b e t h e r e f l e c t i o n p o i n t$ $o f t h e l i g h t r a y a n d t h e r e f o r e A M$ $i s t h e b i s e c t o r o f a n g l e ∠ B A C .$ $w h e n w e c o n s i d e r n o t o n l y p o i n t A,$ $b u t a l s o o t h e r v e r t e x e s, w e w i l l$ $c o n c l u d e t h a t t h e t r i a n g l e h a s o p t i m u m$ $p e r i m e t e r w h e n M i s o n t h e b i s e c t o r s$ $o f a l l a n g l e s o f t h e t r i a n g l e, t h a t$ $m e a n s M i s t h e c e n t e r o f i t s i n c i r c l e .$
	Commented by mr W last updated on 23/Jun/19

	Commented by mr W last updated on 23/Jun/19

	$(s e e d i a g r a m a b o v e)$ $w e c a n a l s o c o n s i d e r l i k e t h i s :$ $p o i n t A l i e s o n c i r c l e w i t h c e n t e r M .$ $w e k n o w t h e l o c u s o f a p o i n t, w h o s e$ $s u m o f d i s t a n c e s t o B a n d C i s$ $c o n s t a n t, i s a n e l l i p s e w i t h f o c u s e s$ $a t p o i n t B a n d C . i n f i n i t e s u c h$ $e l l i p s e s a r e p o s s i b l e . t h e s u m o f t h e$ $d i s t a n c e s A B + A C i s m a x i m u m,$ $w h e n A a l s o l i e s o n s u c h a n e l l i p s e$ $w h i c h t o u c h e s t h e c i r c l e w i t h c e n t e r M .$ $i n t h i s c a s e A M i s a l s o a n o r m a l$ $o f t h e e l l i p s e . w e k n o w a l i g h t r a y$ $f r o m a f o c u s o f a n e l l i p s e p a s s e s a l s o$ $t h r o u g h t h e o t h e r f o c u s a f t e r r e f l e c t i o n$ $o n t h e e l l i p s e, i . e . t h e n o r m a l a t$ $p o i n t A i s t h e a n g l e b i s e c t o r o f t h e$ $l i g h t r a y B A a n d A C, s e e a l s o$ $f o l l o w i n g d i a g r a m .$
	Commented by mr W last updated on 23/Jun/19

	Commented by mr W last updated on 23/Jun/19

	$d u e t o t h i s c o n s i d e r a t i o n i t h i n k t h e$ $t r i a n g l e w e s e a r c h i s t h a t o n e w h o s e$ $i n c i r c l e c e n t e r i s t h e p o i n t M .$ $w e {d o n}^{'} t n e e d t o a p p l y c a l c u l u s m e t h o d$ $l i k e \frac{\partial P}{\partial θ} = 0 a n d \frac{\partial P}{\partial φ} = 0 .$
	Commented by ajfour last updated on 23/Jun/19

	$P l e n t i f u l e v i d e n c e, S i r . T h a n k s$ $a l o t . B u t y e t a n a n a l y t i c a l w a y$ $t o p r o v e t h i s {i s n}^{'} t e a s y (i t r i e d)!$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum