Question and Answers Forum
Question Number 62571 by Joel122 last updated on 23/Jun/19
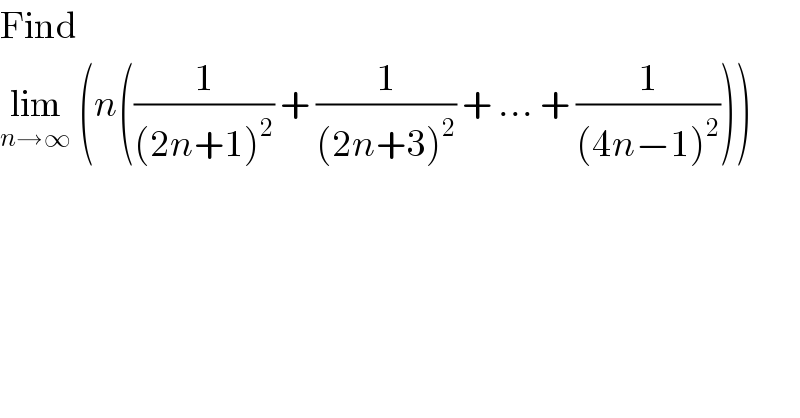
Commented by Prithwish sen last updated on 23/Jun/19
![lim_(n→∞) (1/n) [(l/((2+(1/n))^2 ))+(1/((2+(3/n))^2 )) +....+(1/((2+((2n−1)/n))^2 ))] = lim_(n→∞) (1/n)Σ_(r=1) ^n (1/((2+((2r−1)/n))^2 )) Putn=(1/h) n→∞ ⇒h→0 = lim_(h→0) h Σ_(r=1) ^n (1/((2+2rh)^2 )) =∫_0 ^1 (dx/((2+2x)^2 )) ∵nh=1=1−0 = (1/4)[−(1/((1+x)))]_0 ^1 =(1/4)[−(1/2)+1] =(1/8)](Q62594.png)
Commented by Joel122 last updated on 23/Jun/19

Commented by Tony Lin last updated on 23/Jun/19
![=lim_(n→∞) ((1/2)×(2/n)((1/((2+(1/n))^2 ))+(1/((2+(3/n))^2 ))+...+(1/((4−(1/n))^2 )))) =(1/2)∫_2 ^4 (1/x^2 )dx =(1/2)[−(1/x)]_2 ^4 =−(1/8)+(1/4) =(1/8)](Q62582.png)
Commented by JDamian last updated on 23/Jun/19

Commented by Tony Lin last updated on 23/Jun/19
![The definite integral of a continuous function f(x) over the interval[a , b] ,denoted by ∫_a ^b f(x)dx, is the limit of Riemann sum as the number of subdivisions approaches infinity i.e ∫_a ^b f(x)dx=lim_(n→∞) Σ_(k=1) ^n △xf(x_k ) where △x=((b−a)/n) and x_k =a+k△x now we have △x=(2/n) , means the constant width of the rectangle, and x_k is the x value of the right edge of the k^(th) rectangle,from x_1 =2+(1/n) to x_n = 4−(1/n) ,then f(x_k ) will give us the height of each rectangle ,and here f(x)=(1/x^2 ) , so the area of the k^(th) rectangle is (2/n)×(1/((2+(2/n)k)^2 )) , and we sum that for values of k from 1 to n R(n)=lim_(n→∞) Σ_(k=1) ^n (1/((2+(2/n)k)^2 ))×(2/n) now we can represent the actual area as a limit: ∫_(2 ) ^4 (1/x^2 )dx=lim_(n→∞) Σ_(k=1) ^n (1/((2+(2/n)k)^2 ))×(2/n)=(1/4) but now it gives (1/n) not (2/n) , so it needs to be multiplied by (1/2)](Q62606.png)
Commented by Joel122 last updated on 24/Jun/19