Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 62613 by necx1 last updated on 23/Jun/19

Commented by Prithwish sen last updated on 23/Jun/19

$$=\int \frac{({\mathrm{x}}^2+1)({\mathrm{x}}^2-1)\mathrm{dx}}{{\mathrm{x}}^3\sqrt{\frac{{({\mathrm{x}}^2+1)}^2-{\mathrm{x}}^2}{{\mathrm{x}}^2}}}$$$$=\int \frac{(\mathrm{x}+\frac{1}{\mathrm{x}})(1-\frac{1}{{\mathrm{x}}^2})\mathrm{dx}}{\sqrt{{(\mathrm{x}+\frac{1}{\mathrm{x}})}^2-1}}$$$$=\int \frac{\mathrm{u}\mathrm{du}}{\sqrt{{\mathrm{u}}^2-1}}\mathrm{putting}\mathrm{x}+\frac{1}{\mathrm{x}}=\mathrm{u}$$$$=\sqrt{{\mathrm{u}}^2-1}+\mathrm{C}$$$$=\frac{1}{\mathrm{x}}\sqrt{{\mathrm{x}}^4+{\mathrm{x}}^2+1}+\mathrm{C}$$$$\mathrm{please}\mathrm{check}.$$$$$$

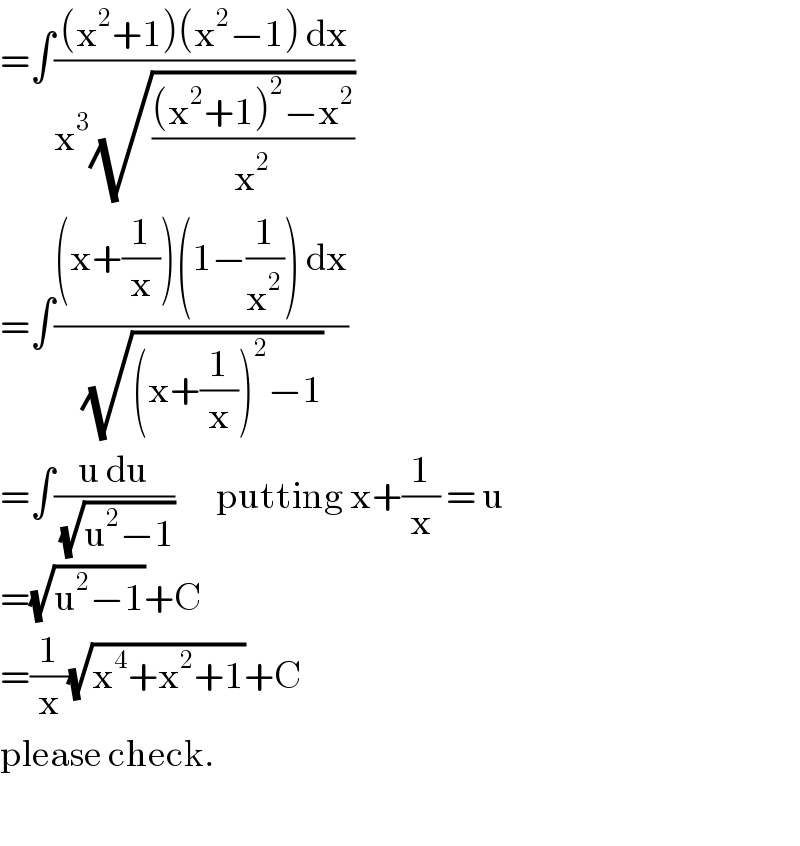
Commented by mathmax by abdo last updated on 24/Jun/19

$$letA=\int \frac{sinx+xcosx}{xsinx}dx\Rightarrow A=\int \frac{dx}{x}+\int \frac{cosx}{sinx}dx$$$$=ln\mid x\mid +ln\mid sinx\mid +c.$$

Answered by tanmay last updated on 23/Jun/19

$$\int \frac{x^2-\frac{1}{x^2}}{\sqrt{x^4+x^2+1}}dx$$$$\int \frac{x^2-\frac{1}{x^2}}{\sqrt{x^2(x^2+1+\frac{1}{x^2})}}dx$$$$\int \frac{x-\frac{1}{x^3}}{\sqrt{x^2+\frac{1}{x^2}+1}}dx$$$$t^2=x^2+\frac{1}{x^2}+1$$$$2t\times \frac{dt}{dx}=2x-\frac{2}{x^3}\to sotdt=(x-\frac{1}{x^3})dx$$$$\int \frac{tdt}{t}$$$$t+c$$$$=\sqrt{x^2+\frac{1}{x^2}+1}+c$$$$$$

Answered by som(math1967) last updated on 23/Jun/19

$$\int \frac{x^4-1}{x^2\sqrt{x^4+x^2+1}}dx$$$$=\int \frac{x^4-1}{x^2\sqrt{x^2(x^2+1+\frac{1}{x^2})}}dx$$$$=\int \frac{(x^4-1)dx}{x^3\sqrt{(x^2+\frac{1}{x^2}+1)}}$$$$=\int \frac{(x-\frac{1}{x^3})dx}{\sqrt{x^2+\frac{1}{x^2}+1}}$$$$let(x^2+\frac{1}{x^2}+1)=z^2\therefore 2(x-\frac{1}{x^3})dx=2zdz$$$$\therefore \int \frac{zdz}{z}=z+C=\sqrt{x^2+\frac{1}{x^2}+1}+C$$$$=\frac{\sqrt{x^4+x^2+1}}{x}+C\left(ans\right)$$$$$$

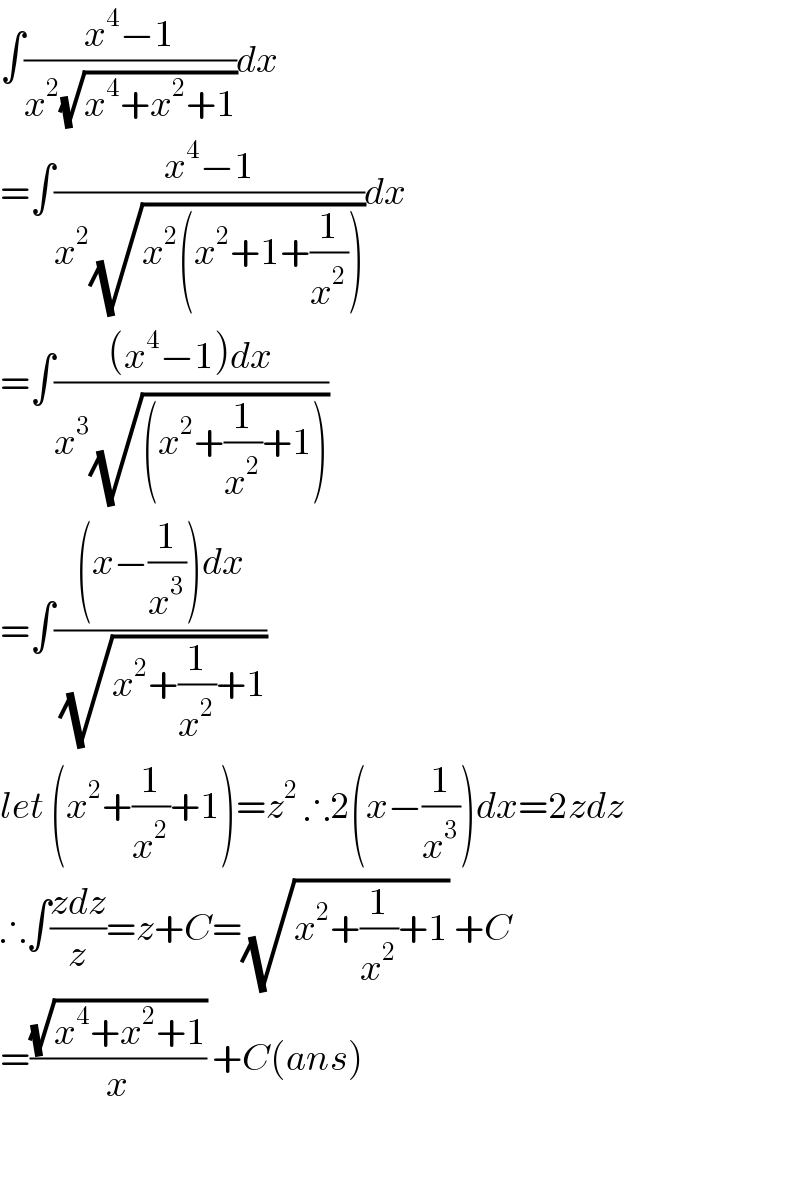
Commented by necx1 last updated on 29/Jun/19

$$youpeoplearejustsowonderful.Thank$$$$yousomuch.$$

Answered by MJS last updated on 23/Jun/19

$${\mathrm{there}}^{\prime }\mathrm{s}\mathrm{a}\mathrm{trick}:$$$$\int \frac{x^4-1}{x^2\sqrt{x^4+x^2+1}}dx=$$$$\int (\frac{x^4-1}{x^2\sqrt{x^4+x^2+1}}+\frac{\sqrt{x^4+x^2+1}}{x^2}-\frac{\sqrt{x^4+x^2+1}}{x^2})dx=$$$$=\int \frac{2x^2+1}{\sqrt{x^4+x^2+1}}dx-\int \frac{\sqrt{x^4+x^2+1}}{x^2}dx$$$$\mathrm{now}\mathrm{solve}\mathrm{the}{2}^{\mathrm{nd}}\mathrm{integral}\mathrm{by}\mathrm{parts}$$$$\int u^{\prime }v=uv-\int {uv}^{\prime }$$$$u^{\prime }=\frac{1}{x^2}\Rightarrow u=-\frac{1}{x}$$$$v=\sqrt{x^4+x^2+1}\Rightarrow v^{\prime }=\frac{2x^3+x}{\sqrt{x^4+x^2+1}}$$$$-\int \frac{\sqrt{x^4+x^2+1}}{x^2}dx=\frac{\sqrt{x^4+x^2+1}}{x}-\int \frac{2x^2+1}{\sqrt{x^4+x^2+1}}dx$$$$\Rightarrow$$$$\int \frac{x^4-1}{x^2\sqrt{x^4+x^2+1}}dx=\frac{\sqrt{x^4+x^2+1}}{x}+C$$

Commented by som(math1967) last updated on 24/Jun/19

$$Nicesir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com