Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 62653 by aliesam last updated on 23/Jun/19

∫x(arctan(x))^2 dx ∫((x e^(arctan(x)) )/((1+x^2 )^(3/2) )) dx ∫((arcsin(x))/(√(1+x))) dx

$$\int\mathrm{x}\left(\mathrm{arctan}\left(\mathrm{x}\right)\right)^{\mathrm{2}} \:\mathrm{dx} \\ $$$$ \\ $$$$\int\frac{\mathrm{x}\:\mathrm{e}^{\mathrm{arctan}\left(\mathrm{x}\right)} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\mathrm{dx} \\ $$$$ \\ $$$$\int\frac{\mathrm{arcsin}\left(\mathrm{x}\right)}{\sqrt{\mathrm{1}+\mathrm{x}}}\:\mathrm{dx} \\ $$

Commented by mathmax by abdo last updated on 24/Jun/19

let I =∫ x arctan^2 x dx by parts u^′ =x and v =arctan^2 x ⇒ I =(x^2 /2) arctan^2 x − ∫ (x^2 /2) ((2arctanx)/(1+x^2 )) dx = (((x arctanx)^2 )/2) −∫ (((1+x^2 −1) arctanx)/(1+x^2 ))dx =(((xarctanx)^2 )/2) −∫ arctan(x)dx +∫ ((arctan(x))/(1+x^2 ))dx ∫ arctan(x)dx =_(by parts) x arctan(x)−∫ (x/(1+x^2 ))dx=x arctan(x)−(1/2)ln(1+x^2 )+c_0 let A =∫ ((arctanx)/(1+x^2 ))dx by parts u^′ =(1/(1+x^2 )) and v =arctan(x) ⇒ A =(arctan(x))^2 −∫ ((arctan(x))/(1+x^2 ))dx ⇒2A =(arctan(x))^2 ⇒ A =(1/2) arctan^2 (x) ⇒ I =(((x arctan(x))^2 )/2) −x arctan(x) +(1/2)ln(1+x^2 ) +(1/2) arctan^2 (x) +C .

$${let}\:{I}\:=\int\:\:{x}\:{arctan}^{\mathrm{2}} {x}\:{dx}\:\:\:\:{by}\:{parts}\:{u}^{'} \:={x}\:{and}\:{v}\:={arctan}^{\mathrm{2}} {x}\:\Rightarrow \\ $$$${I}\:=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:{arctan}^{\mathrm{2}} {x}\:−\:\int\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\frac{\mathrm{2}{arctanx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:=\:\frac{\left({x}\:{arctanx}\right)^{\mathrm{2}} }{\mathrm{2}}\:−\int\:\frac{\left(\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}\right)\:{arctanx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\left({xarctanx}\right)^{\mathrm{2}} }{\mathrm{2}}\:−\int\:{arctan}\left({x}\right){dx}\:+\int\:\:\:\frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\int\:\:{arctan}\left({x}\right){dx}\:=_{{by}\:{parts}} \:\:\:{x}\:{arctan}\left({x}\right)−\int\:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}={x}\:{arctan}\left({x}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \:\right)+{c}_{\mathrm{0}} \\ $$$${let}\:{A}\:=\int\:\:\frac{{arctanx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\:{by}\:{parts}\:{u}^{'} \:=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{and}\:{v}\:={arctan}\left({x}\right)\:\Rightarrow \\ $$$${A}\:=\left({arctan}\left({x}\right)\right)^{\mathrm{2}} \:−\int\:\:\frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\Rightarrow\mathrm{2}{A}\:=\left({arctan}\left({x}\right)\right)^{\mathrm{2}} \:\Rightarrow \\ $$$${A}\:=\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}^{\mathrm{2}} \left({x}\right)\:\Rightarrow \\ $$$${I}\:=\frac{\left({x}\:{arctan}\left({x}\right)\right)^{\mathrm{2}} }{\mathrm{2}}\:−{x}\:{arctan}\left({x}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:+\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}^{\mathrm{2}} \left({x}\right)\:+{C}\:. \\ $$

Commented by aliesam last updated on 24/Jun/19

thanks sir

$$\mathrm{thanks}\:\mathrm{sir}\: \\ $$

Commented by mathmax by abdo last updated on 24/Jun/19

let A = ∫ ((arcsinx)/(√(1+x))) dx changement (√(1+x))=t give 1+x =t^2 ⇒x=t^2 −1 and A =∫ ((arcsin(t^2 −1))/t) (2t)dt =−2 ∫ arcsin(1−t^2 ) dt by parts ∫ arcsin(1−t^2 )dt = t arcsin(1−t^2 )−∫ ((t (−2t))/(√(1−(1−t^2 )^2 ))) dt =t arcsin(1−t^2 ) +2 ∫ (t^2 /(√(1−(1−t^2 )^2 ))) dt changement 1−t^2 =sinα ⇒−2tdt =cosαdα t =(√(1−sinα)) ⇒ ∫ (t^2 /(√(1−(1−t^2 )^2 ))) dt =−(1/2)∫ ((√(1−sinα))/(cosα)) cos(α)dα =−∫ (√(1−sin(α)))dα =−∫ (√(1−cos((π/2)−α)))dα =−∫ (√(2sin^2 ((π/4)−(α/2))))dα =−(√2)∫ sin((π/4)−(α/2))dα =−2(√2)cos((π/4)−(α/2)) +c ⇒ A = −2(t arcsin(1−t^2 ) −4 (√2)cos((π/4) −(α/2))) +c =−2(√(1+x)) arcsin(−x)+8(√2)cos((π/4)−(1/2)arcsin(−x)) +c =2(√(1+x))arcsin(x) +8(√2)cos((π/4) +(1/2)arcsinx) +c .

$${let}\:{A}\:=\:\int\:\:\:\frac{{arcsinx}}{\sqrt{\mathrm{1}+{x}}}\:{dx}\:\:\:{changement}\:\:\sqrt{\mathrm{1}+{x}}={t}\:{give}\:\mathrm{1}+{x}\:={t}^{\mathrm{2}} \:\Rightarrow{x}={t}^{\mathrm{2}} −\mathrm{1}\:{and} \\ $$$${A}\:=\int\:\frac{{arcsin}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{{t}}\:\left(\mathrm{2}{t}\right){dt}\:=−\mathrm{2}\:\int\:{arcsin}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\:{dt} \\ $$$${by}\:{parts}\:\int\:\:\:{arcsin}\left(\mathrm{1}−{t}^{\mathrm{2}} \right){dt}\:=\:{t}\:{arcsin}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)−\int\:\:\frac{{t}\:\left(−\mathrm{2}{t}\right)}{\sqrt{\mathrm{1}−\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }}\:{dt} \\ $$$$={t}\:{arcsin}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\:+\mathrm{2}\:\int\:\:\:\:\frac{{t}^{\mathrm{2}} }{\sqrt{\mathrm{1}−\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }}\:{dt}\:\:{changement}\:\mathrm{1}−{t}^{\mathrm{2}} \:={sin}\alpha\:\Rightarrow−\mathrm{2}{tdt}\:={cos}\alpha{d}\alpha \\ $$$${t}\:=\sqrt{\mathrm{1}−{sin}\alpha}\:\Rightarrow \\ $$$$\int\:\:\frac{{t}^{\mathrm{2}} }{\sqrt{\mathrm{1}−\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }}\:{dt}\:=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\:\frac{\sqrt{\mathrm{1}−{sin}\alpha}}{{cos}\alpha}\:{cos}\left(\alpha\right){d}\alpha\:=−\int\:\sqrt{\mathrm{1}−{sin}\left(\alpha\right)}{d}\alpha \\ $$$$=−\int\:\sqrt{\mathrm{1}−{cos}\left(\frac{\pi}{\mathrm{2}}−\alpha\right)}{d}\alpha\:=−\int\:\sqrt{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{2}}\right)}{d}\alpha \\ $$$$=−\sqrt{\mathrm{2}}\int\:\:{sin}\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{2}}\right){d}\alpha\:=−\mathrm{2}\sqrt{\mathrm{2}}{cos}\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{2}}\right)\:+{c}\:\Rightarrow \\ $$$${A}\:=\:−\mathrm{2}\left({t}\:{arcsin}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\:−\mathrm{4}\:\sqrt{\mathrm{2}}{cos}\left(\frac{\pi}{\mathrm{4}}\:−\frac{\alpha}{\mathrm{2}}\right)\right)\:+{c} \\ $$$$=−\mathrm{2}\sqrt{\mathrm{1}+{x}}\:{arcsin}\left(−{x}\right)+\mathrm{8}\sqrt{\mathrm{2}}{cos}\left(\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}{arcsin}\left(−{x}\right)\right)\:+{c} \\ $$$$=\mathrm{2}\sqrt{\mathrm{1}+{x}}{arcsin}\left({x}\right)\:+\mathrm{8}\sqrt{\mathrm{2}}{cos}\left(\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}{arcsinx}\right)\:+{c}\:. \\ $$

Commented by mathmax by abdo last updated on 24/Jun/19

let I =∫ ((x e^(arctan(x)) )/((1+x^2 )^(3/2) ))dx changement x =tanθ give I =∫ ((e^θ tan(θ))/((1+tan^2 θ)^(3/2) )) (1+tan^2 θ)dθ = ∫ e^θ tanθ cosθ dθ =∫ sinθ e^θ =Im( ∫ e^(iθ +θ) dθ) but ∫ e^((1+i)θ) dθ =(1/(1+i)) e^((1+i)θ) =(e^θ /(1+i)){ cosθ +isinθ} =e^θ ((1−i)/2)(cosθ +isinθ) =(e^θ /2){cosθ +isinθ −icosθ +sinθ} =(e^θ /2){ cosθ +sinθ +i(sinθ −cosθ)} ⇒∫ sinθ e^θ dθ =(e^θ /2)(sinθ −cosθ) +c ⇒ I = (1/2) e^(arctan(x)) { sin(arctanx)−cos(arctanx)} +c =(1/2) e^(arctan(x)) { (x/(√(1+x^2 ))) −(1/(√(1+x^2 )))} +c =((x−1)/(2(√(1+x^2 )))) e^(arctan(x)) +c .

$${let}\:{I}\:=\int\:\:\frac{{x}\:{e}^{{arctan}\left({x}\right)} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{dx}\:\:{changement}\:{x}\:={tan}\theta\:{give} \\ $$$${I}\:=\int\:\:\:\frac{{e}^{\theta} \:{tan}\left(\theta\right)}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta\:=\:\int\:\:{e}^{\theta} \:{tan}\theta\:{cos}\theta\:{d}\theta\:=\int\:{sin}\theta\:{e}^{\theta} \\ $$$$={Im}\left(\:\int\:\:{e}^{{i}\theta\:+\theta} \:{d}\theta\right)\:\:{but}\:\: \\ $$$$\int\:{e}^{\left(\mathrm{1}+{i}\right)\theta} {d}\theta\:=\frac{\mathrm{1}}{\mathrm{1}+{i}}\:{e}^{\left(\mathrm{1}+{i}\right)\theta} \:=\frac{{e}^{\theta} }{\mathrm{1}+{i}}\left\{\:{cos}\theta\:+{isin}\theta\right\} \\ $$$$={e}^{\theta} \frac{\mathrm{1}−{i}}{\mathrm{2}}\left({cos}\theta\:+{isin}\theta\right)\:=\frac{{e}^{\theta} }{\mathrm{2}}\left\{{cos}\theta\:+{isin}\theta\:−{icos}\theta\:\:+{sin}\theta\right\} \\ $$$$=\frac{{e}^{\theta} }{\mathrm{2}}\left\{\:{cos}\theta\:+{sin}\theta\:+{i}\left({sin}\theta\:−{cos}\theta\right)\right\}\:\Rightarrow\int\:{sin}\theta\:{e}^{\theta} \:{d}\theta\:=\frac{{e}^{\theta} }{\mathrm{2}}\left({sin}\theta\:−{cos}\theta\right)\:+{c}\:\Rightarrow \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{{arctan}\left({x}\right)} \left\{\:{sin}\left({arctanx}\right)−{cos}\left({arctanx}\right)\right\}\:+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{{arctan}\left({x}\right)} \left\{\:\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:−\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right\}\:+{c}\:=\frac{{x}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{e}^{{arctan}\left({x}\right)} \:\:\:\:+{c}\:. \\ $$$$ \\ $$

Answered by Smail last updated on 24/Jun/19

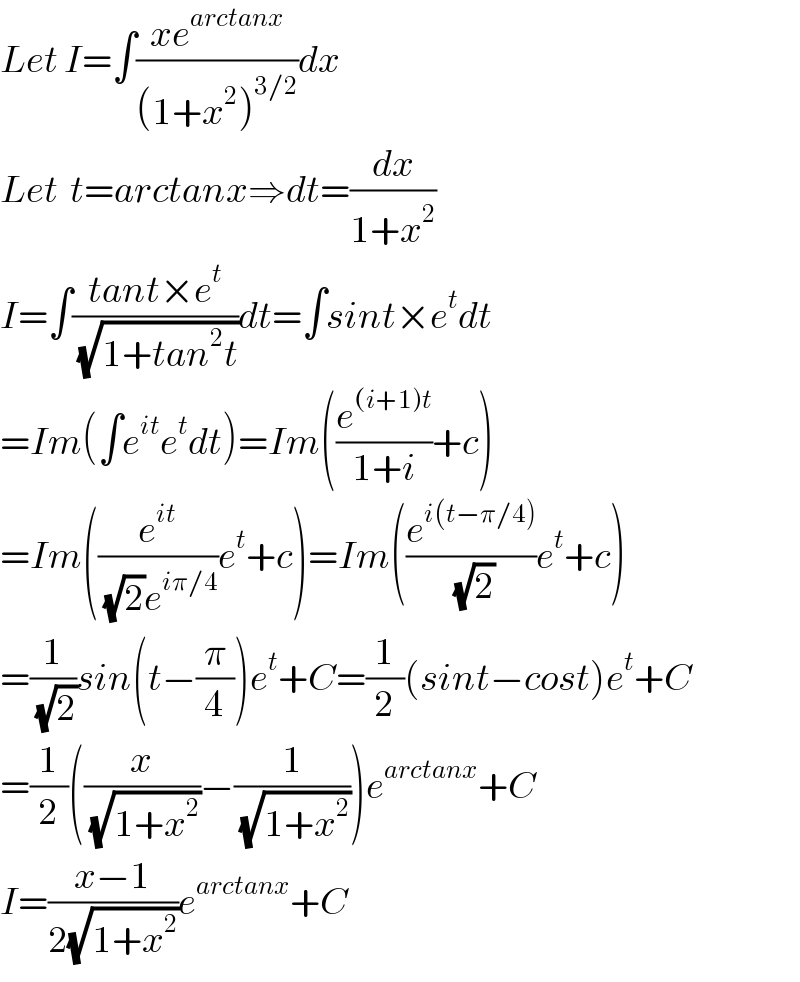
Let I=∫((xe^(arctanx) )/((1+x^2 )^(3/2) ))dx Let t=arctanx⇒dt=(dx/(1+x^2 )) I=∫((tant×e^t )/(√(1+tan^2 t)))dt=∫sint×e^t dt =Im(∫e^(it) e^t dt)=Im((e^((i+1)t) /(1+i))+c) =Im((e^(it) /((√2)e^(iπ/4) ))e^t +c)=Im((e^(i(t−π/4)) /(√2))e^t +c) =(1/(√2))sin(t−(π/4))e^t +C=(1/2)(sint−cost)e^t +C =(1/2)((x/(√(1+x^2 )))−(1/(√(1+x^2 ))))e^(arctanx) +C I=((x−1)/(2(√(1+x^2 ))))e^(arctanx) +C

$${Let}\:{I}=\int\frac{{xe}^{{arctanx}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }{dx} \\ $$$${Let}\:\:{t}={arctanx}\Rightarrow{dt}=\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${I}=\int\frac{{tant}×{e}^{{t}} }{\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {t}}}{dt}=\int{sint}×{e}^{{t}} {dt} \\ $$$$={Im}\left(\int{e}^{{it}} {e}^{{t}} {dt}\right)={Im}\left(\frac{{e}^{\left({i}+\mathrm{1}\right){t}} }{\mathrm{1}+{i}}+{c}\right) \\ $$$$={Im}\left(\frac{{e}^{{it}} }{\sqrt{\mathrm{2}}{e}^{{i}\pi/\mathrm{4}} }{e}^{{t}} +{c}\right)={Im}\left(\frac{{e}^{{i}\left({t}−\pi/\mathrm{4}\right)} }{\sqrt{\mathrm{2}}}{e}^{{t}} +{c}\right) \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{sin}\left({t}−\frac{\pi}{\mathrm{4}}\right){e}^{{t}} +{C}=\frac{\mathrm{1}}{\mathrm{2}}\left({sint}−{cost}\right){e}^{{t}} +{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}−\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right){e}^{{arctanx}} +{C} \\ $$$${I}=\frac{{x}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{e}^{{arctanx}} +{C} \\ $$

Commented by Smail last updated on 24/Jun/19

B=∫((arcsinx)/(√(1+x)))dx By parts u=arcsinx⇒u′=(1/(√(1−x^2 ))) v′=(1/(√(1+x)))⇒v=2(√(1+x)) B=2(√(1+x))arcsinx−2∫(√((1+x)/(1−x^2 )))dx+c =2(√(1+x))arcsinx−2∫(dx/(√(1−x)))+c B=2(√(1+x))arcsinx+4(√(1−x))+C

$${B}=\int\frac{{arcsinx}}{\sqrt{\mathrm{1}+{x}}}{dx} \\ $$$${By}\:{parts} \\ $$$${u}={arcsinx}\Rightarrow{u}'=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${v}'=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{x}}}\Rightarrow{v}=\mathrm{2}\sqrt{\mathrm{1}+{x}} \\ $$$${B}=\mathrm{2}\sqrt{\mathrm{1}+{x}}{arcsinx}−\mathrm{2}\int\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}+{c} \\ $$$$=\mathrm{2}\sqrt{\mathrm{1}+{x}}{arcsinx}−\mathrm{2}\int\frac{{dx}}{\sqrt{\mathrm{1}−{x}}}+{c} \\ $$$${B}=\mathrm{2}\sqrt{\mathrm{1}+{x}}{arcsinx}+\mathrm{4}\sqrt{\mathrm{1}−{x}}+{C} \\ $$

Commented by aliesam last updated on 24/Jun/19

thank you sir god bless you

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\: \\ $$$$\mathrm{god}\:\mathrm{bless}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com