
Question and Answers Forum
Question Number 62657 by mathmax by abdo last updated on 24/Jun/19
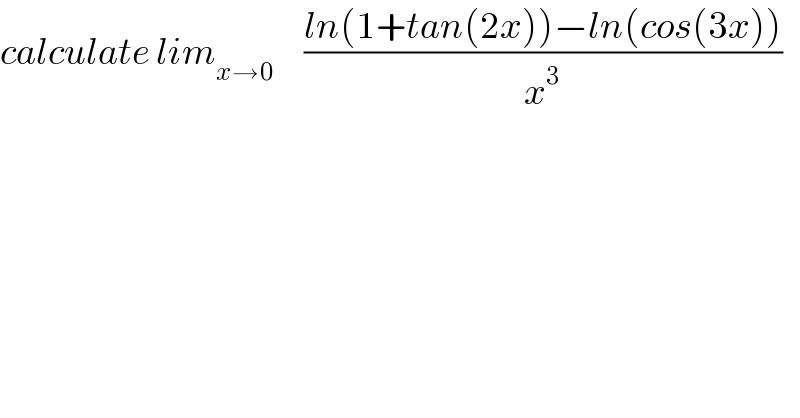
Commented by mathmax by abdo last updated on 24/Jun/19

Commented by MJS last updated on 24/Jun/19
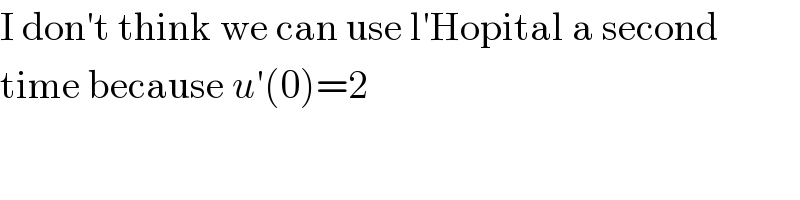
Answered by MJS last updated on 24/Jun/19
![lim_(x→0) ((ln (1+tan 2x) −ln cos 3x)/x^3 )= =lim_(x→0) (((d/dx)[ln (1+tan 2x) −ln cos 3x])/((d/dx)[x^3 ]))= =lim_(x→0) (((4/(1+cos 4x +sin 4x))+3tan 3x)/(3x^(2 ) ))=(2/0) ⇒ undefined](Q62663.png)
| ||
Question and Answers Forum | ||
Question Number 62657 by mathmax by abdo last updated on 24/Jun/19 | ||
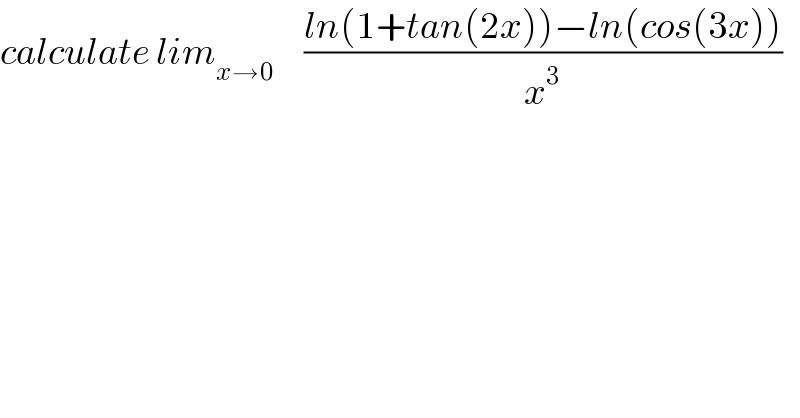 | ||
Commented by mathmax by abdo last updated on 24/Jun/19 | ||
 | ||
Commented by MJS last updated on 24/Jun/19 | ||
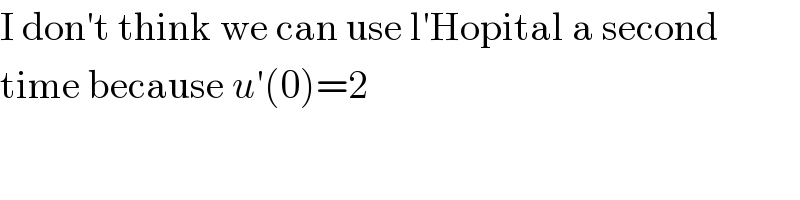 | ||
Answered by MJS last updated on 24/Jun/19 | ||
![lim_(x→0) ((ln (1+tan 2x) −ln cos 3x)/x^3 )= =lim_(x→0) (((d/dx)[ln (1+tan 2x) −ln cos 3x])/((d/dx)[x^3 ]))= =lim_(x→0) (((4/(1+cos 4x +sin 4x))+3tan 3x)/(3x^(2 ) ))=(2/0) ⇒ undefined](Q62663.png) | ||
| ||