Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 62773 by ajfour last updated on 25/Jun/19

Commented by ajfour last updated on 25/Jun/19

Find maximum area of quadrilateral in yellow in terms of r and R.

$${Find}\:{maximum}\:{area}\:{of}\:{quadrilateral} \\ $$$${in}\:{yellow}\:{in}\:{terms}\:{of}\:{r}\:{and}\:{R}. \\ $$

Answered by ajfour last updated on 25/Jun/19

Commented by ajfour last updated on 25/Jun/19

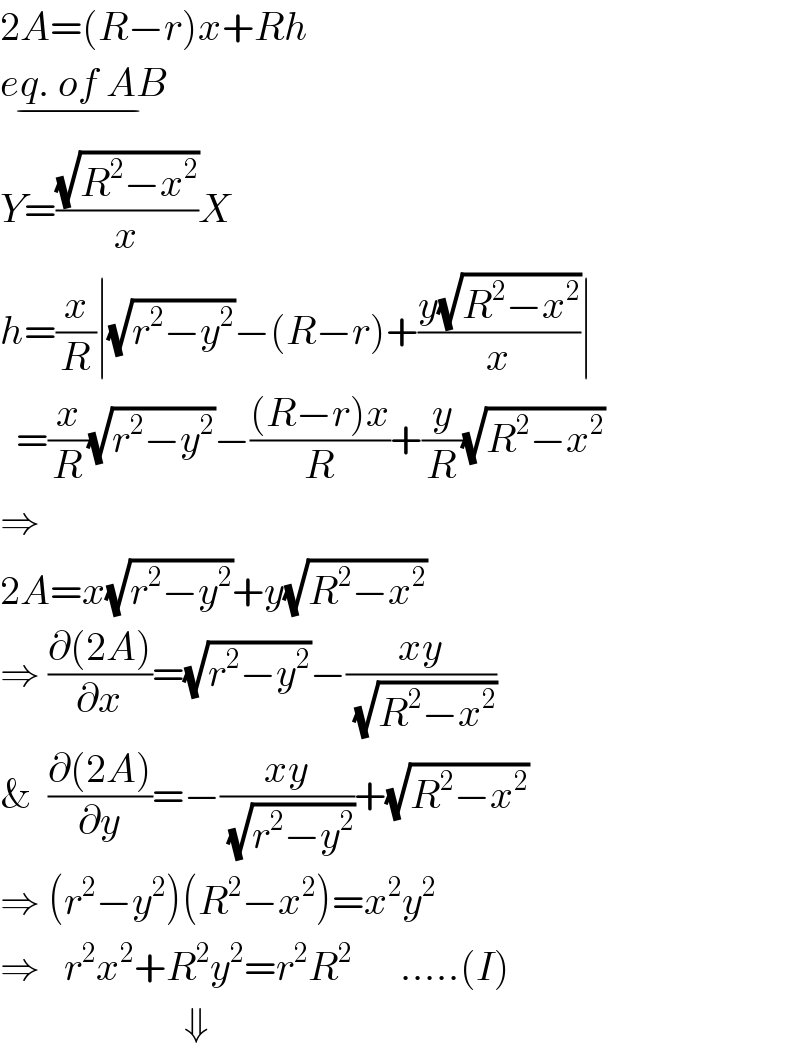
2A=(R−r)x+Rh eq. of AB_(−) Y=((√(R^2 −x^2 ))/x)X h=(x/R)∣(√(r^2 −y^2 ))−(R−r)+((y(√(R^2 −x^2 )))/x)∣ =(x/R)(√(r^2 −y^2 ))−(((R−r)x)/R)+(y/R)(√(R^2 −x^2 )) ⇒ 2A=x(√(r^2 −y^2 ))+y(√(R^2 −x^2 )) ⇒ ((∂(2A))/∂x)=(√(r^2 −y^2 ))−((xy)/(√(R^2 −x^2 ))) & ((∂(2A))/∂y)=−((xy)/(√(r^2 −y^2 )))+(√(R^2 −x^2 )) ⇒ (r^2 −y^2 )(R^2 −x^2 )=x^2 y^2 ⇒ r^2 x^2 +R^2 y^2 =r^2 R^2 .....(I) ⇓

$$\mathrm{2}{A}=\left({R}−{r}\right){x}+{Rh} \\ $$$$\underset{−} {{eq}.\:{of}\:{AB}} \\ $$$${Y}=\frac{\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }}{{x}}{X} \\ $$$${h}=\frac{{x}}{{R}}\mid\sqrt{{r}^{\mathrm{2}} −{y}^{\mathrm{2}} }−\left({R}−{r}\right)+\frac{{y}\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }}{{x}}\mid \\ $$$$\:\:=\frac{{x}}{{R}}\sqrt{{r}^{\mathrm{2}} −{y}^{\mathrm{2}} }−\frac{\left({R}−{r}\right){x}}{{R}}+\frac{{y}}{{R}}\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$$\mathrm{2}{A}={x}\sqrt{{r}^{\mathrm{2}} −{y}^{\mathrm{2}} }+{y}\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\frac{\partial\left(\mathrm{2}{A}\right)}{\partial{x}}=\sqrt{{r}^{\mathrm{2}} −{y}^{\mathrm{2}} }−\frac{{xy}}{\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }} \\ $$$$\&\:\:\frac{\partial\left(\mathrm{2}{A}\right)}{\partial{y}}=−\frac{{xy}}{\sqrt{{r}^{\mathrm{2}} −{y}^{\mathrm{2}} }}+\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\left({r}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)\left({R}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)={x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{r}^{\mathrm{2}} {x}^{\mathrm{2}} +{R}^{\mathrm{2}} {y}^{\mathrm{2}} ={r}^{\mathrm{2}} {R}^{\mathrm{2}} \:\:\:\:\:\:.....\left({I}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Downarrow\: \\ $$

Commented by mr W last updated on 25/Jun/19

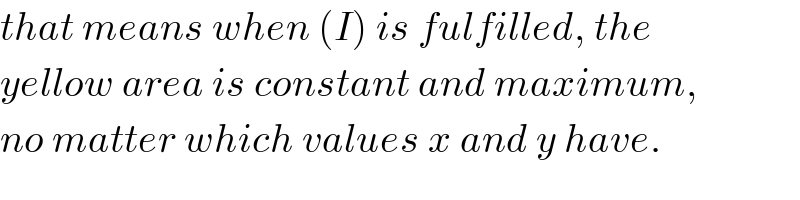
that means when (I) is fulfilled, the yellow area is constant and maximum, no matter which values x and y have.

$${that}\:{means}\:{when}\:\left({I}\right)\:{is}\:{fulfilled},\:{the} \\ $$$${yellow}\:{area}\:{is}\:{constant}\:{and}\:{maximum},\: \\ $$$${no}\:{matter}\:{which}\:{values}\:{x}\:{and}\:{y}\:{have}. \\ $$

Commented by mr W last updated on 25/Jun/19

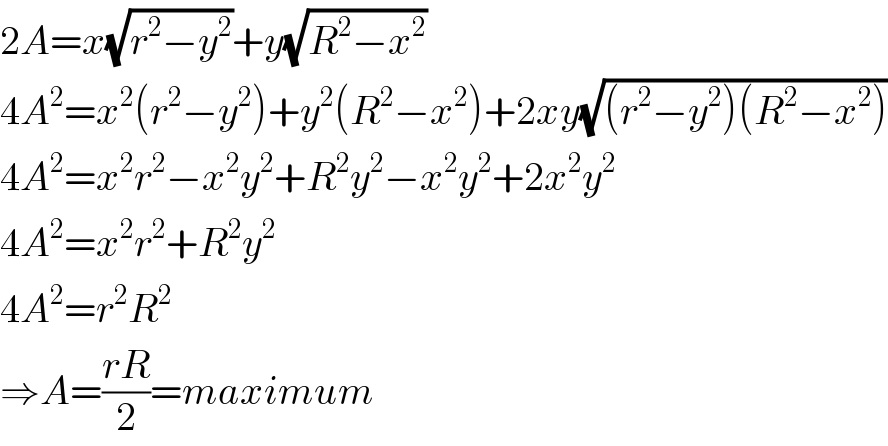
2A=x(√(r^2 −y^2 ))+y(√(R^2 −x^2 )) 4A^2 =x^2 (r^2 −y^2 )+y^2 (R^2 −x^2 )+2xy(√((r^2 −y^2 )(R^2 −x^2 ))) 4A^2 =x^2 r^2 −x^2 y^2 +R^2 y^2 −x^2 y^2 +2x^2 y^2 4A^2 =x^2 r^2 +R^2 y^2 4A^2 =r^2 R^2 ⇒A=((rR)/2)=maximum

$$\mathrm{2}{A}={x}\sqrt{{r}^{\mathrm{2}} −{y}^{\mathrm{2}} }+{y}\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$\mathrm{4}{A}^{\mathrm{2}} ={x}^{\mathrm{2}} \left({r}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)+{y}^{\mathrm{2}} \left({R}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)+\mathrm{2}{xy}\sqrt{\left({r}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)\left({R}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)} \\ $$$$\mathrm{4}{A}^{\mathrm{2}} ={x}^{\mathrm{2}} {r}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{R}^{\mathrm{2}} {y}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$\mathrm{4}{A}^{\mathrm{2}} ={x}^{\mathrm{2}} {r}^{\mathrm{2}} +{R}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$\mathrm{4}{A}^{\mathrm{2}} ={r}^{\mathrm{2}} {R}^{\mathrm{2}} \\ $$$$\Rightarrow{A}=\frac{{rR}}{\mathrm{2}}={maximum} \\ $$

Commented by ajfour last updated on 25/Jun/19

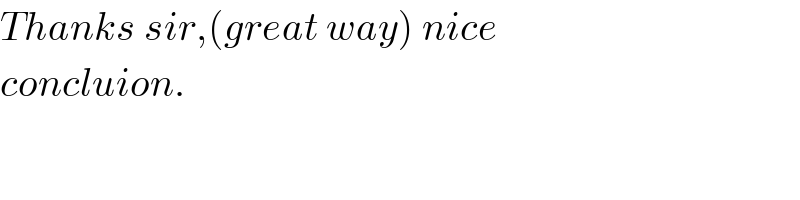
Thanks sir,(great way) nice concluion.

$${Thanks}\:{sir},\left({great}\:{way}\right)\:{nice}\: \\ $$$${concluion}. \\ $$

Commented by mr W last updated on 25/Jun/19

Commented by mr W last updated on 25/Jun/19

Answered by mr W last updated on 25/Jun/19

Commented by mr W last updated on 25/Jun/19

take point B at any angle θ. such that area of AOB is maximum, tangent AD should be parallel to OB. we get ∠ACO=θ and OB⊥AC. Δ_(ABC) =((AC×(OB+CO×sin θ))/2)=((r[R+(R−r)sin θ])/2) Δ_(AOC) =((r(R−r)sin θ)/2) A=yellow area=Δ_(ABC) −Δ_(AOC) =((r[R+(R−r)sin θ])/2)−((r(R−r)sin θ)/2) =((rR)/2)=constant independent from θ since OB⊥AC, we can directly see: yellow area A=((AC×OB)/2)=((rR)/2)

$${take}\:{point}\:{B}\:{at}\:{any}\:{angle}\:\theta. \\ $$$${such}\:{that}\:{area}\:{of}\:{AOB}\:{is}\:{maximum}, \\ $$$${tangent}\:{AD}\:{should}\:{be}\:{parallel}\:{to}\:{OB}. \\ $$$${we}\:{get}\:\angle{ACO}=\theta\:{and}\:{OB}\bot{AC}. \\ $$$$\Delta_{{ABC}} =\frac{{AC}×\left({OB}+{CO}×\mathrm{sin}\:\theta\right)}{\mathrm{2}}=\frac{{r}\left[{R}+\left({R}−{r}\right)\mathrm{sin}\:\theta\right]}{\mathrm{2}} \\ $$$$\Delta_{{AOC}} =\frac{{r}\left({R}−{r}\right)\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$${A}={yellow}\:{area}=\Delta_{{ABC}} −\Delta_{{AOC}} \\ $$$$=\frac{{r}\left[{R}+\left({R}−{r}\right)\mathrm{sin}\:\theta\right]}{\mathrm{2}}−\frac{{r}\left({R}−{r}\right)\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$$=\frac{{rR}}{\mathrm{2}}={constant}\:{independent}\:{from}\:\theta \\ $$$$ \\ $$$${since}\:{OB}\bot{AC},\:{we}\:{can}\:{directly}\:{see}: \\ $$$${yellow}\:{area}\:{A}=\frac{{AC}×{OB}}{\mathrm{2}}=\frac{{rR}}{\mathrm{2}} \\ $$

Commented by ajfour last updated on 25/Jun/19

Good Magic, best explained! Thanks Sir.

$${Good}\:\mathcal{M}{agic},\:{best}\:{explained}! \\ $$$${Thanks}\:{Sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com