
Question and Answers Forum
Question Number 62811 by mathmax by abdo last updated on 25/Jun/19
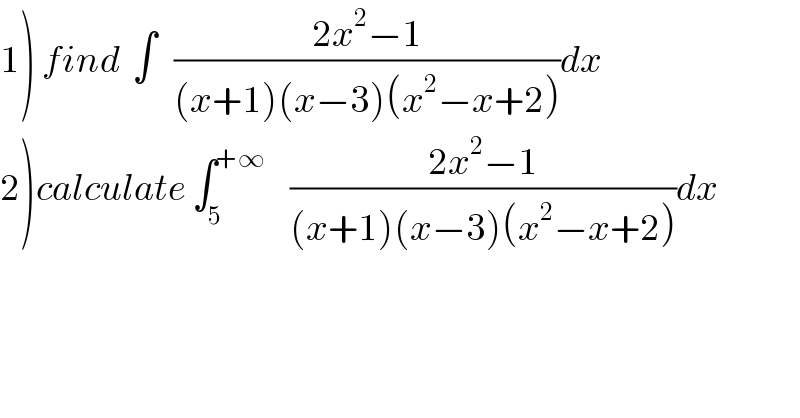
Commented by Prithwish sen last updated on 25/Jun/19
![1)((2x^2 −1)/((x+1)(x−3)(x^2 −x+2))) =(A/(x+1)) + (B/(x−3)) +((Cx+D)/(x^2 −x+2)) By calculating we get ∫[((−1)/(16(x+1))) +((17)/(32(x−3))) −((15(2x−1))/(32(x^2 −x+2))) −(1/(16(x^2 −x+2))) ] dx = −(1/(16)) ln(x+1)+((17)/(32)) ln(x−3) −((15)/(32)) ln(x^2 −x+2)−(1/(8(√7))) tan^(−1) ((2x−1)/(√7)) +C waiting for feedbacks](Q62834.png)
Commented by mathmax by abdo last updated on 26/Jun/19

| ||
Question and Answers Forum | ||
Question Number 62811 by mathmax by abdo last updated on 25/Jun/19 | ||
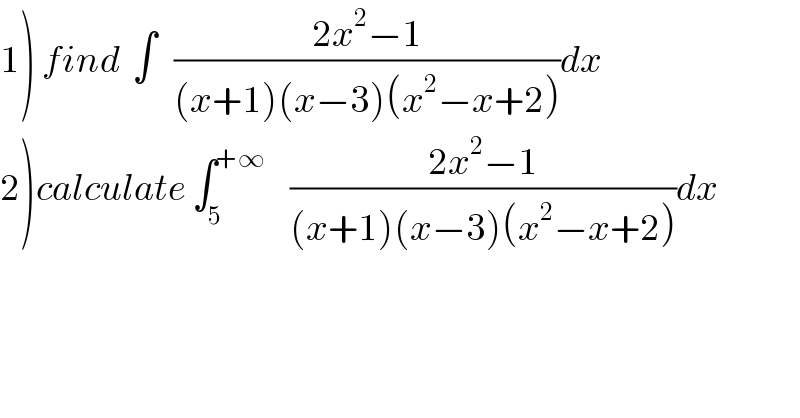 | ||
Commented by Prithwish sen last updated on 25/Jun/19 | ||
![1)((2x^2 −1)/((x+1)(x−3)(x^2 −x+2))) =(A/(x+1)) + (B/(x−3)) +((Cx+D)/(x^2 −x+2)) By calculating we get ∫[((−1)/(16(x+1))) +((17)/(32(x−3))) −((15(2x−1))/(32(x^2 −x+2))) −(1/(16(x^2 −x+2))) ] dx = −(1/(16)) ln(x+1)+((17)/(32)) ln(x−3) −((15)/(32)) ln(x^2 −x+2)−(1/(8(√7))) tan^(−1) ((2x−1)/(√7)) +C waiting for feedbacks](Q62834.png) | ||
Commented by mathmax by abdo last updated on 26/Jun/19 | ||
 | ||