
Question Number 62814 by Cheyboy last updated on 25/Jun/19

Commented by Cheyboy last updated on 25/Jun/19
$${Please}\:{help}\:{me}\:{with}\:{these}\:{question} \\ $$
Commented by mathmax by abdo last updated on 25/Jun/19
![3) let I =∫_0 ^∞ ((16 arctan(x))/(1+x^2 )) dx ⇒ I =16 ∫_0 ^∞ ((arctan(x))/(1+x^2 ))dx by parts ∫_0 ^∞ ((arctan(x))/(1+x^2 ))dx =[arctan^2 x]_0 ^(+∞) −∫_0 ^∞ ((arctan(x))/(1+x^2 )) dx =(π^2 /4) −∫_0 ^∞ ((arctanx)/(1+x^2 ))dx 2 ∫_0 ^∞ ((arctan(x))/(1+x^2 ))dx =(π^2 /4) ⇒∫_0 ^∞ ((arctan(x))/(1+x^2 ))dx =(π^2 /8) ⇒I =16.(π^2 /8) ⇒ I =2π^2 .](Q62817.png)
$$\left.\mathrm{3}\right)\:{let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{16}\:{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:\Rightarrow\:{I}\:=\mathrm{16}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\:{by}\:{parts} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\left[{arctan}^{\mathrm{2}} {x}\right]_{\mathrm{0}} ^{+\infty} \:−\int_{\mathrm{0}} ^{\infty} \:\frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:−\int_{\mathrm{0}} ^{\infty} \frac{{arctanx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow{I}\:=\mathrm{16}.\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow\:{I}\:=\mathrm{2}\pi^{\mathrm{2}} \:. \\ $$
Commented by Prithwish sen last updated on 25/Jun/19
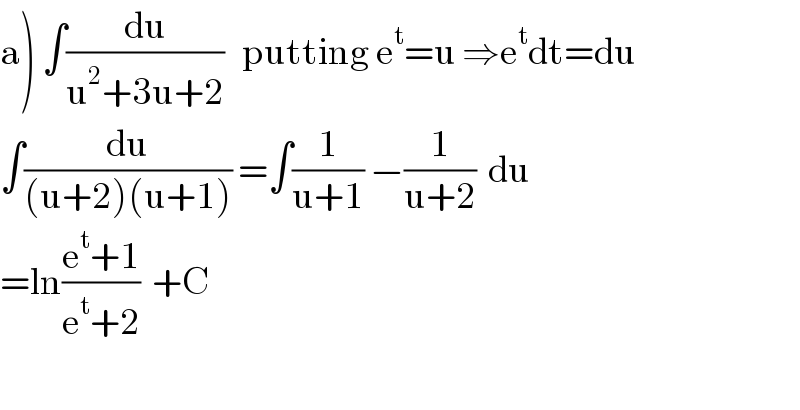
$$\left.\mathrm{a}\right)\:\int\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\mathrm{3u}+\mathrm{2}}\:\:\:\mathrm{putting}\:\mathrm{e}^{\mathrm{t}} =\mathrm{u}\:\Rightarrow\mathrm{e}^{\mathrm{t}} \mathrm{dt}=\mathrm{du} \\ $$$$\int\frac{\mathrm{du}}{\left(\mathrm{u}+\mathrm{2}\right)\left(\mathrm{u}+\mathrm{1}\right)}\:=\int\frac{\mathrm{1}}{\mathrm{u}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{u}+\mathrm{2}}\:\:\mathrm{du} \\ $$$$=\mathrm{ln}\frac{\mathrm{e}^{\mathrm{t}} +\mathrm{1}}{\mathrm{e}^{\mathrm{t}} +\mathrm{2}}\:\:+\mathrm{C} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 25/Jun/19
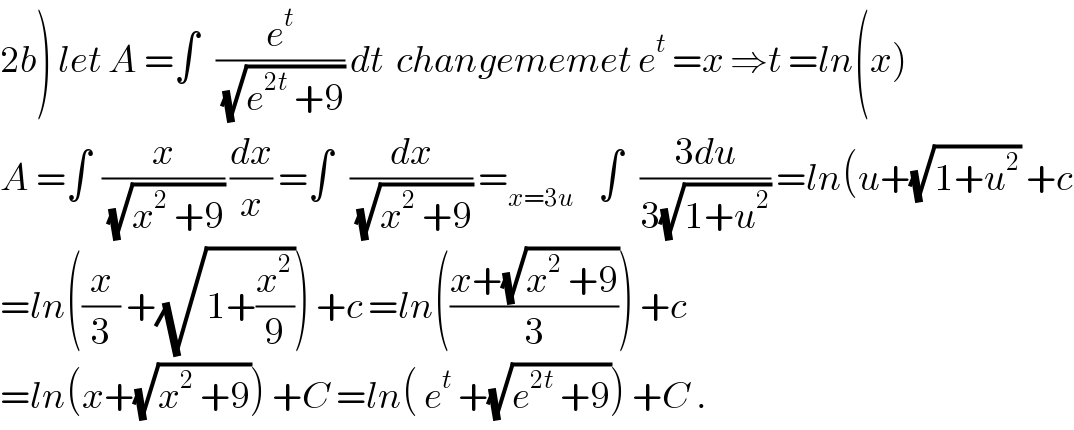
$$\left.\mathrm{2}{b}\right)\:{let}\:{A}\:=\int\:\:\:\frac{{e}^{{t}} }{\sqrt{{e}^{\mathrm{2}{t}} \:+\mathrm{9}}}\:{dt}\:\:{changememet}\:{e}^{{t}} \:={x}\:\Rightarrow{t}\:={ln}\left({x}\right) \\ $$$${A}\:=\int\:\:\frac{{x}}{\sqrt{{x}^{\mathrm{2}} \:+\mathrm{9}}}\:\frac{{dx}}{{x}}\:=\int\:\:\:\frac{{dx}}{\sqrt{{x}^{\mathrm{2}} \:+\mathrm{9}}}\:=_{{x}=\mathrm{3}{u}} \:\:\:\:\int\:\:\:\frac{\mathrm{3}{du}}{\mathrm{3}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}\:={ln}\left({u}+\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\:+{c}\right. \\ $$$$={ln}\left(\frac{{x}}{\mathrm{3}}\:+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{9}}}\right)\:+{c}\:={ln}\left(\frac{{x}+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{9}}}{\mathrm{3}}\right)\:+{c} \\ $$$$={ln}\left({x}+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{9}}\right)\:+{C}\:={ln}\left(\:{e}^{{t}} \:+\sqrt{{e}^{\mathrm{2}{t}} \:+\mathrm{9}}\right)\:+{C}\:. \\ $$
Commented by Cheyboy last updated on 25/Jun/19

$$\mathbb{THANK}\:\mathbb{YOU}\:\mathbb{ALL}\:\mathbb{SIRS}\: \\ $$$$\mathbb{FOR}\:\mathbb{HELP}\:\mathbb{WELL}\:\mathbb{APPRECIATED} \\ $$
Commented by Prithwish sen last updated on 25/Jun/19
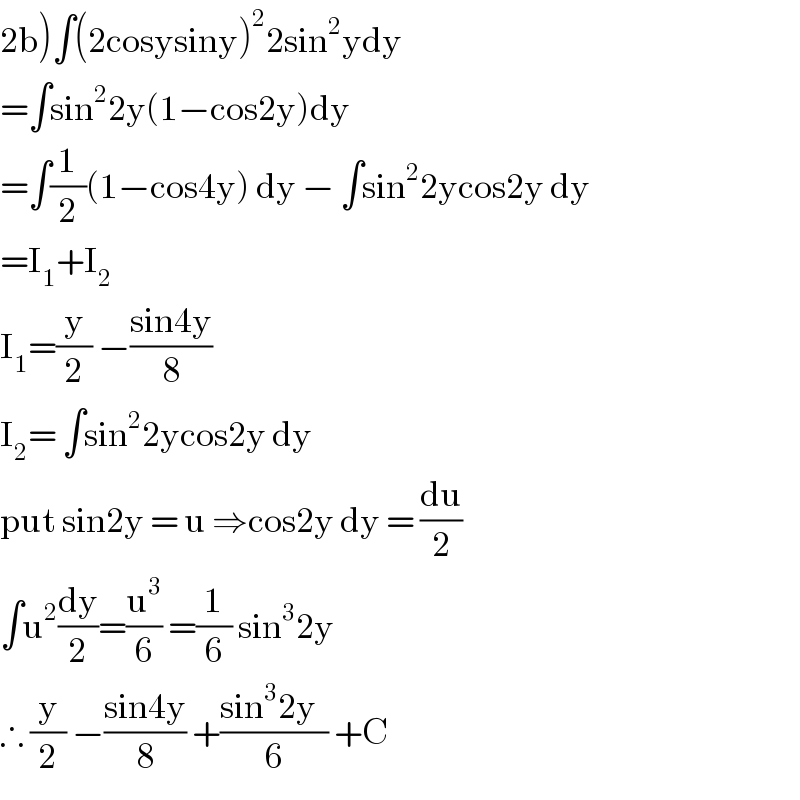
$$\left.\mathrm{2b}\right)\int\left(\mathrm{2cosysiny}\right)^{\mathrm{2}} \mathrm{2sin}^{\mathrm{2}} \mathrm{ydy} \\ $$$$=\int\mathrm{sin}^{\mathrm{2}} \mathrm{2y}\left(\mathrm{1}−\mathrm{cos2y}\right)\mathrm{dy} \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos4y}\right)\:\mathrm{dy}\:−\:\int\mathrm{sin}^{\mathrm{2}} \mathrm{2ycos2y}\:\mathrm{dy} \\ $$$$=\mathrm{I}_{\mathrm{1}} +\mathrm{I}_{\mathrm{2}} \\ $$$$\mathrm{I}_{\mathrm{1}} =\frac{\mathrm{y}}{\mathrm{2}}\:−\frac{\mathrm{sin4y}}{\mathrm{8}} \\ $$$$\mathrm{I}_{\mathrm{2}} =\:\int\mathrm{sin}^{\mathrm{2}} \mathrm{2ycos2y}\:\mathrm{dy}\:\:\: \\ $$$$\mathrm{put}\:\mathrm{sin2y}\:=\:\mathrm{u}\:\Rightarrow\mathrm{cos2y}\:\mathrm{dy}\:=\:\frac{\mathrm{du}}{\mathrm{2}} \\ $$$$\int\mathrm{u}^{\mathrm{2}} \frac{\mathrm{dy}}{\mathrm{2}}=\frac{\mathrm{u}^{\mathrm{3}} }{\mathrm{6}}\:=\frac{\mathrm{1}}{\mathrm{6}}\:\mathrm{sin}^{\mathrm{3}} \mathrm{2y} \\ $$$$\therefore\:\frac{\mathrm{y}}{\mathrm{2}}\:−\frac{\mathrm{sin4y}}{\mathrm{8}}\:+\frac{\mathrm{sin}^{\mathrm{3}} \mathrm{2y}\:\:}{\mathrm{6}}\:+\mathrm{C} \\ $$
Commented by Cheyboy last updated on 25/Jun/19

$${Thank}\:{alot}\:{sir} \\ $$
Commented by Cheyboy last updated on 25/Jun/19

Commented by mathmax by abdo last updated on 26/Jun/19
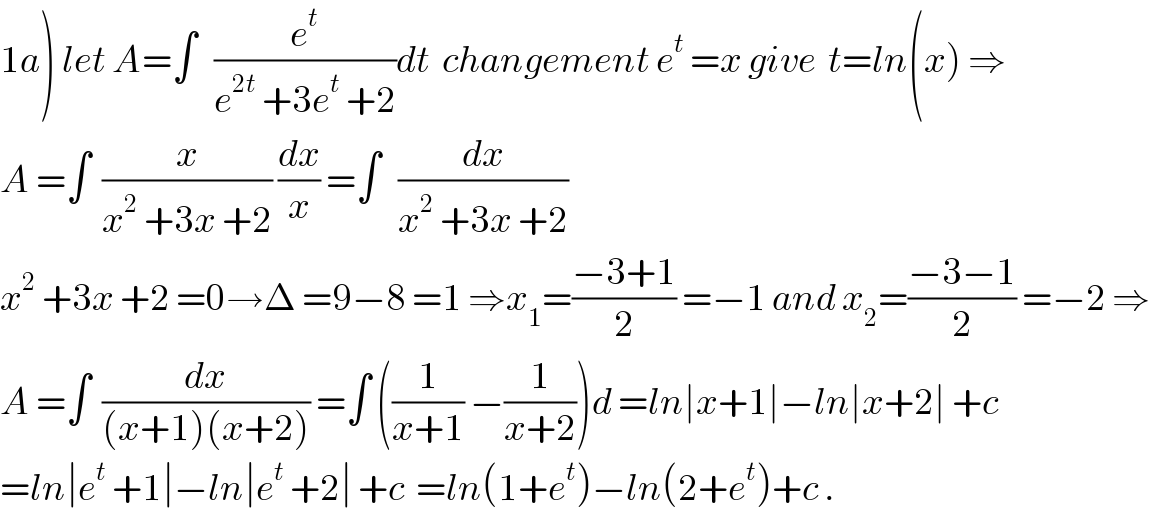
$$\left.\mathrm{1}{a}\right)\:{let}\:{A}=\int\:\:\:\frac{{e}^{{t}} }{{e}^{\mathrm{2}{t}} \:+\mathrm{3}{e}^{{t}} \:+\mathrm{2}}{dt}\:\:{changement}\:{e}^{{t}} \:={x}\:{give}\:\:{t}={ln}\left({x}\right)\:\Rightarrow \\ $$$${A}\:=\int\:\:\frac{{x}}{{x}^{\mathrm{2}} \:+\mathrm{3}{x}\:+\mathrm{2}}\:\frac{{dx}}{{x}}\:=\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{3}{x}\:+\mathrm{2}} \\ $$$${x}^{\mathrm{2}} \:+\mathrm{3}{x}\:+\mathrm{2}\:=\mathrm{0}\rightarrow\Delta\:=\mathrm{9}−\mathrm{8}\:=\mathrm{1}\:\Rightarrow{x}_{\mathrm{1}} =\frac{−\mathrm{3}+\mathrm{1}}{\mathrm{2}}\:=−\mathrm{1}\:{and}\:{x}_{\mathrm{2}} =\frac{−\mathrm{3}−\mathrm{1}}{\mathrm{2}}\:=−\mathrm{2}\:\Rightarrow \\ $$$${A}\:=\int\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)}\:=\int\:\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}\:−\frac{\mathrm{1}}{{x}+\mathrm{2}}\right){d}\:={ln}\mid{x}+\mathrm{1}\mid−{ln}\mid{x}+\mathrm{2}\mid\:+{c} \\ $$$$={ln}\mid{e}^{{t}} \:+\mathrm{1}\mid−{ln}\mid{e}^{{t}} \:+\mathrm{2}\mid\:+{c}\:\:={ln}\left(\mathrm{1}+{e}^{{t}} \right)−{ln}\left(\mathrm{2}+{e}^{{t}} \right)+{c}\:. \\ $$
Commented by mathmax by abdo last updated on 27/Jun/19
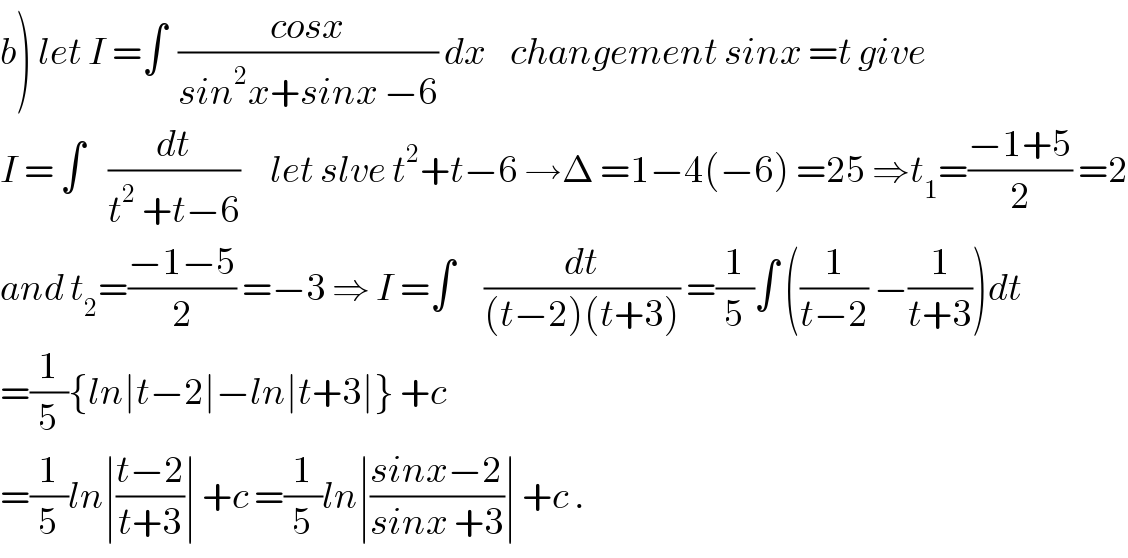
$$\left.{b}\right)\:{let}\:{I}\:=\int\:\:\frac{{cosx}}{{sin}^{\mathrm{2}} {x}+{sinx}\:−\mathrm{6}}\:{dx}\:\:\:\:{changement}\:{sinx}\:={t}\:{give} \\ $$$${I}\:=\:\int\:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+{t}−\mathrm{6}}\:\:\:\:\:{let}\:{slve}\:{t}^{\mathrm{2}} +{t}−\mathrm{6}\:\rightarrow\Delta\:=\mathrm{1}−\mathrm{4}\left(−\mathrm{6}\right)\:=\mathrm{25}\:\Rightarrow{t}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{5}}{\mathrm{2}}\:=\mathrm{2} \\ $$$${and}\:{t}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{5}}{\mathrm{2}}\:=−\mathrm{3}\:\Rightarrow\:{I}\:=\int\:\:\:\:\:\frac{{dt}}{\left({t}−\mathrm{2}\right)\left({t}+\mathrm{3}\right)}\:=\frac{\mathrm{1}}{\mathrm{5}}\int\:\left(\frac{\mathrm{1}}{{t}−\mathrm{2}}\:−\frac{\mathrm{1}}{{t}+\mathrm{3}}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\left\{{ln}\mid{t}−\mathrm{2}\mid−{ln}\mid{t}+\mathrm{3}\mid\right\}\:+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}{ln}\mid\frac{{t}−\mathrm{2}}{{t}+\mathrm{3}}\mid\:+{c}\:=\frac{\mathrm{1}}{\mathrm{5}}{ln}\mid\frac{{sinx}−\mathrm{2}}{{sinx}\:+\mathrm{3}}\mid\:+{c}\:. \\ $$
