Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 62839 by ajfour last updated on 25/Jun/19

Commented by ajfour last updated on 25/Jun/19
$let θ be angle between b and extended c . (c+bcos θ)^2 +b^2 sin^2 θ=r^2 (c+asin θ)^2 +a^2 cos^2 θ=r^2 ⇒ b^2 +c^2 +2bccos θ=r^2 a^2 +c^2 +2acsin θ=r^2 ⇒ 2c(asin θ−bcos θ)=b^2 −a^2 2c(√(a^2 +b^2 ))sin (θ−tan^(−1) (b/a))=b^2 −a^2 ⇒ θ=α+sin^(−1) (p/h) = α+β .....(I) but on adding 2r^2 = a^2 +b^2 +2c^2 +2c(√(a^2 +b^2 ))sin (θ+tan^(−1) (b/a)) ⇒ r^2 =c^2 +((a^2 +b^2 )/2)+(h/2)sin (2α+β) = c^2 +((a^2 +b^2 )/2)+(h/2){((2ab)/(a^2 +b^2 ))×(√(1−(p^2 /h^2 )))+(((2a^2 )/(a^2 +b^2 ))−1)(p/h)} r^2 =c^2 +((a^2 +b^2 )/2)+((ab(√(h^2 −p^2 )))/(a^2 +b^2 ))+(((a^2 −b^2 )p)/(2(a^2 +b^2 ))) r^2 =c^2 +((a^2 +b^2 )/2)−(((b^2 −a^2 )^2 )/(2(a^2 +b^2 )))+((ab)/((a^2 +b^2 )))(√(4c^2 (a^2 +b^2 )−(b^2 −a^2 )^2 )) ⇒ r^2 =c^2 +((2a^2 b^2 )/(a^2 +b^2 ))+((ab)/((a^2 +b^2 )))(√(4c^2 (a^2 +b^2 )−(b^2 −a^2 )^2 )) r=(√(c^2 +((2a^2 b^2 )/(a^2 +b^2 ))+((ab)/((a^2 +b^2 )))(√(4c^2 (a^2 +b^2 )−(b^2 −a^2 )^2 )))) .$
$l e t θ b e a n g l e b e t w e e n b a n d$ $e x t e n d e d c .$ ${(c + b \cos θ)}^{2} + b^{2} \sin^{2} θ = r^{2}$ ${(c + a \sin θ)}^{2} + a^{2} \cos^{2} θ = r^{2}$ $\Rightarrow$ $b^{2} + c^{2} + 2 b c \cos θ = r^{2}$ $a^{2} + c^{2} + 2 a c \sin θ = r^{2}$ $\Rightarrow 2 c (a \sin θ - b \cos θ) = b^{2} - a^{2}$ $2 c \sqrt{a^{2} + b^{2}} \sin (θ - \tan^{- 1} \frac{b}{a}) = b^{2} - a^{2}$ $\Rightarrow θ = α + \sin^{- 1} \frac{p}{h} = α + β . . . . . (I)$ $b u t o n a d d i n g$ $2 r^{2} = a^{2} + b^{2} + 2 c^{2} + 2 c \sqrt{a^{2} + b^{2}} \sin (θ + \tan^{- 1} \frac{b}{a})$ $\Rightarrow r^{2} = c^{2} + \frac{a^{2} + b^{2}}{2} + \frac{h}{2} \sin (2 α + β)$ $= c^{2} + \frac{a^{2} + b^{2}}{2} + \frac{h}{2} {\frac{2 a b}{a^{2} + b^{2}} \times \sqrt{1 - \frac{p^{2}}{h^{2}}} + (\frac{2 a^{2}}{a^{2} + b^{2}} - 1) \frac{p}{h}}$ $r^{2} = c^{2} + \frac{a^{2} + b^{2}}{2} + \frac{a b \sqrt{h^{2} - p^{2}}}{a^{2} + b^{2}} + \frac{(a^{2} - b^{2}) p}{2 (a^{2} + b^{2})}$ $r^{2} = c^{2} + \frac{a^{2} + b^{2}}{2} - \frac{{(b^{2} - a^{2})}^{2}}{2 (a^{2} + b^{2})} + \frac{a b}{(a^{2} + b^{2})} \sqrt{4 c^{2} (a^{2} + b^{2}) - {(b^{2} - a^{2})}^{2}}$ $\Rightarrow r^{2} = c^{2} + \frac{2 a^{2} b^{2}}{a^{2} + b^{2}} + \frac{a b}{(a^{2} + b^{2})} \sqrt{4 c^{2} (a^{2} + b^{2}) - {(b^{2} - a^{2})}^{2}}$ $r = \sqrt{c^{2} + \frac{2 a^{2} b^{2}}{a^{2} + b^{2}} + \frac{a b}{(a^{2} + b^{2})} \sqrt{4 c^{2} (a^{2} + b^{2}) - {(b^{2} - a^{2})}^{2}}} .$
Commented by ajfour last updated on 25/Jun/19

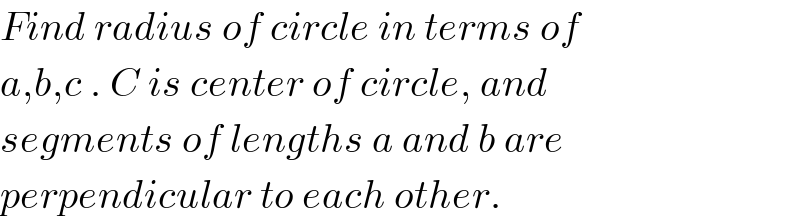
$F i n d r a d i u s o f c i r c l e i n t e r m s o f$ $a, b, c . C i s c e n t e r o f c i r c l e, a n d$ $s e g m e n t s o f l e n g t h s a a n d b a r e$ $p e r p e n d i c u l a r t o e a c h o t h e r .$
Commented by behi83417@gmail.com last updated on 25/Jun/19

$great question, sir Ajfour!$ $waitng for solution (s) . . . . . . . . . .$
	Answered by mr W last updated on 25/Jun/19

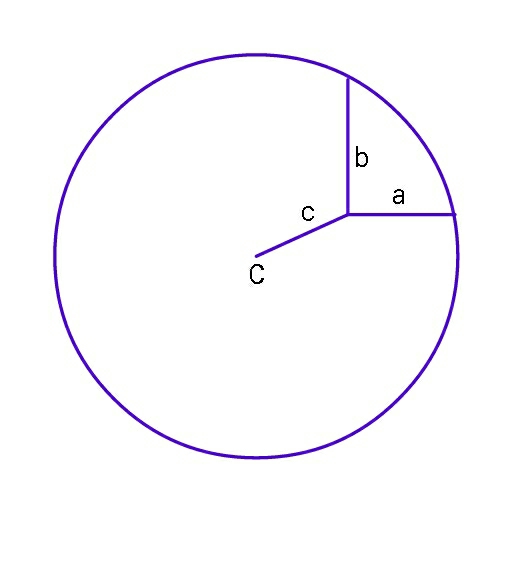
	$r = r a d i u s o f c i r c l e$ $α = a n g l e b e t w e e n a a n d c$ $β = a n g l e b e t w e e n b a n d c$ $α + β + \frac{π}{2} = 2 π$ $\Rightarrow α = 2 π - (\frac{π}{2} + β)$ $\Rightarrow \cos α = - \sin β$ $\Rightarrow \cos^{2} α + \cos^{2} β = 1$ $\cos α = \frac{a^{2} + c^{2} - r^{2}}{2 a c}$ $\cos β = \frac{b^{2} + c^{2} - r^{2}}{2 b c}$ $\Rightarrow {(\frac{a^{2} + c^{2} - r^{2}}{2 a c})}^{2} + {(\frac{b^{2} + c^{2} - r^{2}}{2 b c})}^{2} = 1$ $b^{2} [a^{4} + 2 a^{2} c^{2} + c^{4} - 2 (a^{2} + c^{2}) r^{2} + r^{4}] + a^{2} [b^{4} + 2 b^{2} c^{2} + c^{4} - 2 (b^{2} + c^{2}) r^{2} + r^{4}] = 4 a^{2} b^{2} c^{2}$ $(a^{2} + b^{2}) r^{4} - 2 [2 a^{2} b^{2} + (a^{2} + b^{2}) c^{2}] r^{2} + (a^{2} + b^{2}) (a^{2} b^{2} + c^{4}) = 0$ $\Rightarrow r^{2} = \frac{2 a^{2} b^{2} + (a^{2} + b^{2}) c^{2} + \sqrt{{[2 a^{2} b^{2} + (a^{2} + b^{2}) c^{2}]}^{2} - {(a^{2} + b^{2})}^{2} (a^{2} b^{2} + c^{4})}}{a^{2} + b^{2}}$ $\Rightarrow r^{2} = \frac{2 a^{2} b^{2} + (a^{2} + b^{2}) c^{2} + a b \sqrt{4 (a^{2} + b^{2}) c^{2} - {(a^{2} - b^{2})}^{2}}}{a^{2} + b^{2}}$ $\Rightarrow r = \sqrt{\frac{2 a^{2} b^{2} + (a^{2} + b^{2}) c^{2} + a b \sqrt{4 (a^{2} + b^{2}) c^{2} - {(a^{2} - b^{2})}^{2}}}{a^{2} + b^{2}}}$
	Commented by ajfour last updated on 25/Jun/19

	$T o o g o o d S i r . T h a n k s f o r c o n f i r m i n g .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum