
Question and Answers Forum
Question Number 62869 by aliesam last updated on 26/Jun/19
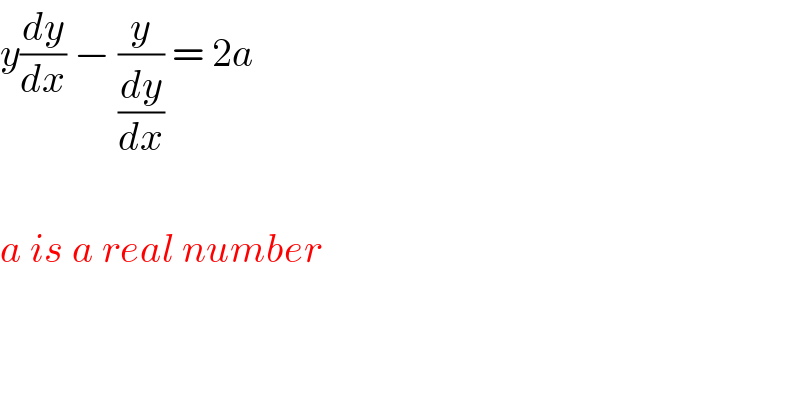
Answered by Hope last updated on 26/Jun/19
![y((dy/dx))^2 −y=2a((dy/dx)) yp^2 −2ap−y=0 p=((2a±(√(4a^2 +4y^2 )))/(2y)) (dy/dx)=((2a±(√(4a^2 +4y^2 )))/(2y)) ((ydy)/(a±(√(a^2 +y^2 ))))=dx t^2 =a^2 +y^2 →tdt=ydy now ∫((ydy)/(a+(√(a^2 +y^2 ))))=∫dx →[considering + sign] ∫((tdt)/(a+t))=∫dx ∫((a+t−a)/(a+t))dt=∫dx ∫dt−a∫(dt/(a+t))=∫dx t−aln(a+t)=x+c (√(a^2 +y^2 )) −aln(a+(√(a^2 +y^2 )) )=x+c if cosider −ve sign ∫((ydy)/(a−(√(a^2 +y^2 ))))=∫dx ∫((tdt)/(a−t))=∫dx ∫((a−t−a)/(a−t))dt=−∫dx ∫dt−a∫(dt/(a−t))=−∫dx ∫dt+∫((adt)/(t−a))=−∫dx t+aln(t−a)=−x+c_1 (√(a^2 +y^2 )) +aln((√(a^2 +y^2 )) −a)=−x+c_1](Q62888.png)
Commented by aliesam last updated on 26/Jun/19

Commented by Hope last updated on 26/Jun/19

Commented by mr W last updated on 26/Jun/19

Commented by Hope last updated on 26/Jun/19

