
Question and Answers Forum
Question Number 62908 by aliesam last updated on 26/Jun/19
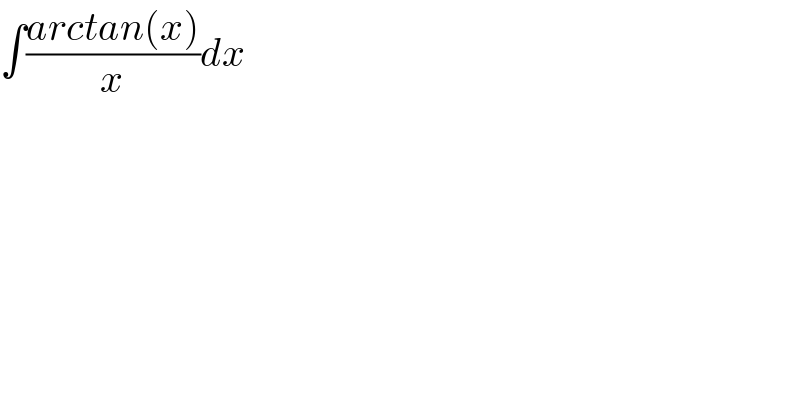
Commented by mathmax by abdo last updated on 26/Jun/19
![for all x from R u→((arctanu)/u)is integrable on ]0,x]let f(t) =∫_0 ^x ((arctan(tu))/u)du we have f^′ (t) =∫_0 ^x arctan(tu)du =_(by parts) [u arctan(tu)]_(u=0) ^(u=x) −∫_0 ^x u(t/(1+t^2 u^2 )) du =x arctan(tx)−(1/(2t)) ∫_0 ^x ((2t^2 u)/(1+t^2 u^2 )) du =xarctan(tx)−(1/(2t))[ ln(1+t^2 u^2 )]_(u=0) ^(u=x) =xarctan(tx)−(1/(2t))ln(1+t^2 x^2 ) ⇒ f(t) =∫_0 ^t x arctan(ux)du −∫_0 ^t ((ln(1+x^2 u^2 ))/(2u)) du +C ⇒ ∫_0 ^x ((arctan(u))/u) du =f(1) =x∫_0 ^1 arctan(ux)du−∫_0 ^1 ((ln(1+x^2 u^2 ))/(2u)) du +C x=0 ⇒C =0 ⇒∫_0 ^x ((arctan(u))/u) du=x ∫_0 ^1 arctan(ux)du−∫_0 ^1 ((ln(1+x^2 u^2 3)/(2u)) du ...be continued....](Q62913.png)
| ||
Question and Answers Forum | ||
Question Number 62908 by aliesam last updated on 26/Jun/19 | ||
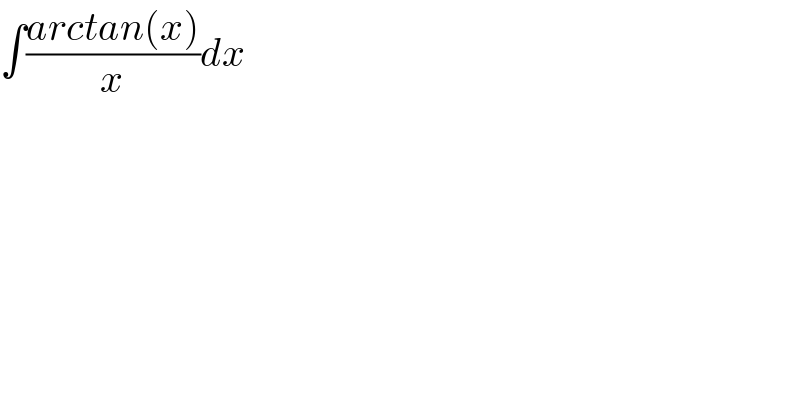 | ||
Commented by mathmax by abdo last updated on 26/Jun/19 | ||
![for all x from R u→((arctanu)/u)is integrable on ]0,x]let f(t) =∫_0 ^x ((arctan(tu))/u)du we have f^′ (t) =∫_0 ^x arctan(tu)du =_(by parts) [u arctan(tu)]_(u=0) ^(u=x) −∫_0 ^x u(t/(1+t^2 u^2 )) du =x arctan(tx)−(1/(2t)) ∫_0 ^x ((2t^2 u)/(1+t^2 u^2 )) du =xarctan(tx)−(1/(2t))[ ln(1+t^2 u^2 )]_(u=0) ^(u=x) =xarctan(tx)−(1/(2t))ln(1+t^2 x^2 ) ⇒ f(t) =∫_0 ^t x arctan(ux)du −∫_0 ^t ((ln(1+x^2 u^2 ))/(2u)) du +C ⇒ ∫_0 ^x ((arctan(u))/u) du =f(1) =x∫_0 ^1 arctan(ux)du−∫_0 ^1 ((ln(1+x^2 u^2 ))/(2u)) du +C x=0 ⇒C =0 ⇒∫_0 ^x ((arctan(u))/u) du=x ∫_0 ^1 arctan(ux)du−∫_0 ^1 ((ln(1+x^2 u^2 3)/(2u)) du ...be continued....](Q62913.png) | ||