Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 62937 by Prithwish sen last updated on 27/Jun/19

$${\int }_0^{\mathrm{x}}\frac{1}{1+{\mathrm{x}}^2}\mathrm{dx}$$

Commented by mathmax by abdo last updated on 27/Jun/19

$${\int }_0^x\frac{dt}{1+t^2}={\left[arctan\left(t\right)\right]}_0^x=arctanx.$$

Commented by Prithwish sen last updated on 27/Jun/19

$$\mathrm{thank}\mathrm{you}\mathrm{sir}$$

Commented by Prithwish sen last updated on 27/Jun/19

$$\mathrm{thank}\mathrm{you}\mathrm{sir}$$

Answered by peter frank last updated on 27/Jun/19

$$letx=\tan \theta \to \theta ={\tan }^{-1}x$$$$dx=\sec {}^2\theta d\theta$$$$\int \frac{\sec {}^2\theta d\theta }{\sec {}^2\theta }$$$$\theta +c$$$${\tan }^{-1}x+c$$$$$$

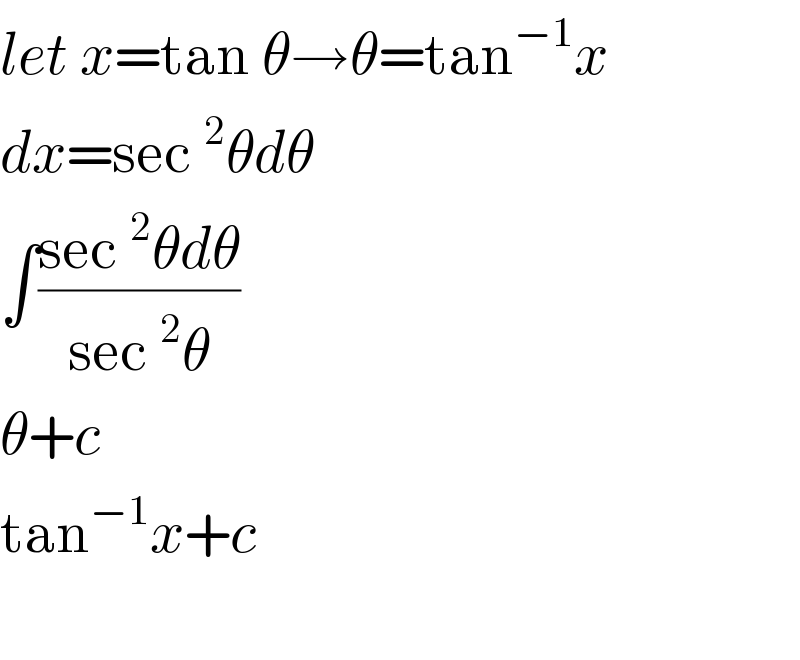
Commented by Prithwish sen last updated on 27/Jun/19

$$\mathrm{thank}\mathrm{you}\mathrm{sir}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com