
Question Number 62981 by hovea cw last updated on 27/Jun/19

Commented by mathmax by abdo last updated on 27/Jun/19
![2) let A =∫_0 ^(2π) ((x∣sin(2x)∣)/(3+sin^2 x)) dx changement x =π +t give A =∫_(−π) ^π (((π+t)∣sin(2t)∣)/(3+sin^2 t)) dt = ∫_(−π) ^0 (((π+t)∣sin(2t)∣)/(3+sin^2 t)) dt +∫_0 ^π (((π+t)∣sin(2t)∣)/(3+sin^2 t)) dt ∫_(−π) ^0 (((π+t)∣sin(2t)∣)/(3+sin^2 t)) dt =_(t=−u) −∫_0 ^π (((π−u)∣sin(2u)∣)/(3+sin^2 u))(−du) ⇒ A = ∫_0 ^π (((π+t+π−t)∣sin(2t)∣)/(3+sin^2 t)) dt =2π ∫_0 ^π ((∣sin(2t)∣)/(3+sin^2 t))dt =_(2t =x) 2π ∫_0 ^(2π) ((∣sin(x)∣)/(3+sin^2 ((x/2)))) (dx/2) =π { ∫_0 ^π ((sinx)/(3+sin^2 ((x/2))))dx +∫_π ^(2π) ((∣sinx∣)/(3+sin^2 ((x/2))))dx} ∫_π ^(2π) ((∣sinx∣)/(3+sin^2 ((x/2))))dx =_(x =π +α) ∫_0 ^π ((sin(α))/(3+sin^2 ((π/2)+(α/2)))) dα =∫_0 ^π ((sin(α))/(3+cos^2 ((α/2))))dα ⇒ A =π { ∫_0 ^π ((sin(x))/(3+sin^2 ((x/2))))dx +∫_0 ^π ((sinx)/(3+cos^2 ((x/2))))dx} =π ∫_0 ^π sinx(7/((3+sin^2 ((x/2)))(3+cos^2 ((x/2))))dx =7π ∫_0 ^π ((sinx)/((3+((1−cosx)/2))(3+((1+cosx)/2))))dx =28π∫_0 ^π sinx{(1/(7−cosx)) +(1/(7+cosx))}dx =28π { ∫_0 ^π ((sinx)/(7−cosx))dx +∫_0 ^π ((sinx)/(7 +cosx))dx} =28π{ [ln∣7−cosx∣]_0 ^π −[ln∣7+cosx∣]_0 ^π } =28π{ ln(8)−ln(6)−ln(6) +ln(8)} =28π{2ln(8)−2ln(6)} =56π{ln(8)−ln(6)} =56π{3ln(2)−ln(2)−ln(3)} ⇒ A =56π{2ln(2)−ln(3)} .](Q62992.png)
$$\left.\mathrm{2}\right)\:{let}\:{A}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{x}\mid{sin}\left(\mathrm{2}{x}\right)\mid}{\mathrm{3}+{sin}^{\mathrm{2}} {x}}\:{dx}\:{changement}\:{x}\:=\pi\:+{t}\:{give} \\ $$$${A}\:=\int_{−\pi} ^{\pi} \:\:\frac{\left(\pi+{t}\right)\mid{sin}\left(\mathrm{2}{t}\right)\mid}{\mathrm{3}+{sin}^{\mathrm{2}} {t}}\:{dt}\:=\:\int_{−\pi} ^{\mathrm{0}} \:\frac{\left(\pi+{t}\right)\mid{sin}\left(\mathrm{2}{t}\right)\mid}{\mathrm{3}+{sin}^{\mathrm{2}} {t}}\:{dt}\:+\int_{\mathrm{0}} ^{\pi} \:\frac{\left(\pi+{t}\right)\mid{sin}\left(\mathrm{2}{t}\right)\mid}{\mathrm{3}+{sin}^{\mathrm{2}} {t}}\:{dt} \\ $$$$\int_{−\pi} ^{\mathrm{0}} \:\frac{\left(\pi+{t}\right)\mid{sin}\left(\mathrm{2}{t}\right)\mid}{\mathrm{3}+{sin}^{\mathrm{2}} {t}}\:{dt}\:=_{{t}=−{u}} \:\:\:−\int_{\mathrm{0}} ^{\pi} \:\frac{\left(\pi−{u}\right)\mid{sin}\left(\mathrm{2}{u}\right)\mid}{\mathrm{3}+{sin}^{\mathrm{2}} {u}}\left(−{du}\right)\:\Rightarrow \\ $$$${A}\:=\:\int_{\mathrm{0}} ^{\pi} \:\frac{\left(\pi+{t}+\pi−{t}\right)\mid{sin}\left(\mathrm{2}{t}\right)\mid}{\mathrm{3}+{sin}^{\mathrm{2}} {t}}\:{dt}\:=\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mid{sin}\left(\mathrm{2}{t}\right)\mid}{\mathrm{3}+{sin}^{\mathrm{2}} {t}}{dt} \\ $$$$=_{\mathrm{2}{t}\:={x}} \:\:\:\:\:\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{\mid{sin}\left({x}\right)\mid}{\mathrm{3}+{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\:\frac{{dx}}{\mathrm{2}}\:=\pi\:\left\{\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{sinx}}{\mathrm{3}+{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{dx}\:+\int_{\pi} ^{\mathrm{2}\pi} \:\:\frac{\mid{sinx}\mid}{\mathrm{3}+{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{dx}\right\} \\ $$$$\int_{\pi} ^{\mathrm{2}\pi} \:\:\frac{\mid{sinx}\mid}{\mathrm{3}+{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{dx}\:=_{{x}\:=\pi\:+\alpha} \:\:\:\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{sin}\left(\alpha\right)}{\mathrm{3}+{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}+\frac{\alpha}{\mathrm{2}}\right)}\:{d}\alpha\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{{sin}\left(\alpha\right)}{\mathrm{3}+{cos}^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}\right)}{d}\alpha\:\Rightarrow \\ $$$${A}\:=\pi\:\left\{\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{sin}\left({x}\right)}{\mathrm{3}+{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{dx}\:+\int_{\mathrm{0}} ^{\pi} \:\:\frac{{sinx}}{\mathrm{3}+{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{dx}\right\} \\ $$$$=\pi\:\int_{\mathrm{0}} ^{\pi} \:{sinx}\frac{\mathrm{7}}{\left(\mathrm{3}+{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)\left(\mathrm{3}+{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right.}{dx}\:=\mathrm{7}\pi\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{sinx}}{\left(\mathrm{3}+\frac{\mathrm{1}−{cosx}}{\mathrm{2}}\right)\left(\mathrm{3}+\frac{\mathrm{1}+{cosx}}{\mathrm{2}}\right)}{dx} \\ $$$$=\mathrm{28}\pi\int_{\mathrm{0}} ^{\pi} \:{sinx}\left\{\frac{\mathrm{1}}{\mathrm{7}−{cosx}}\:+\frac{\mathrm{1}}{\mathrm{7}+{cosx}}\right\}{dx} \\ $$$$=\mathrm{28}\pi\:\left\{\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{sinx}}{\mathrm{7}−{cosx}}{dx}\:+\int_{\mathrm{0}} ^{\pi} \:\frac{{sinx}}{\mathrm{7}\:+{cosx}}{dx}\right\} \\ $$$$=\mathrm{28}\pi\left\{\:\:\left[{ln}\mid\mathrm{7}−{cosx}\mid\right]_{\mathrm{0}} ^{\pi} \:−\left[{ln}\mid\mathrm{7}+{cosx}\mid\right]_{\mathrm{0}} ^{\pi} \right\} \\ $$$$=\mathrm{28}\pi\left\{\:{ln}\left(\mathrm{8}\right)−{ln}\left(\mathrm{6}\right)−{ln}\left(\mathrm{6}\right)\:+{ln}\left(\mathrm{8}\right)\right\}\:=\mathrm{28}\pi\left\{\mathrm{2}{ln}\left(\mathrm{8}\right)−\mathrm{2}{ln}\left(\mathrm{6}\right)\right\} \\ $$$$=\mathrm{56}\pi\left\{{ln}\left(\mathrm{8}\right)−{ln}\left(\mathrm{6}\right)\right\}\:=\mathrm{56}\pi\left\{\mathrm{3}{ln}\left(\mathrm{2}\right)−{ln}\left(\mathrm{2}\right)−{ln}\left(\mathrm{3}\right)\right\}\:\Rightarrow \\ $$$${A}\:=\mathrm{56}\pi\left\{\mathrm{2}{ln}\left(\mathrm{2}\right)−{ln}\left(\mathrm{3}\right)\right\}\:. \\ $$$$ \\ $$
Answered by Hope last updated on 27/Jun/19
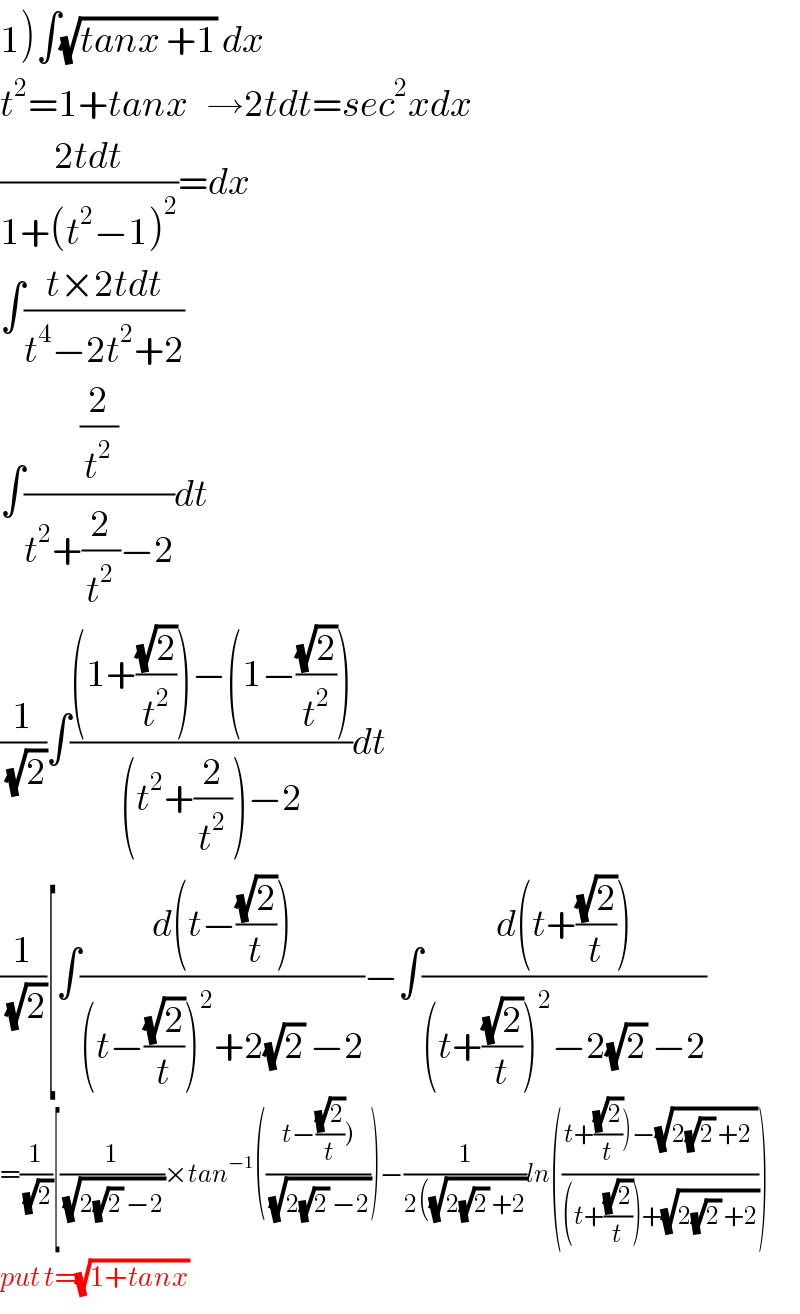
$$\left.\mathrm{1}\right)\int\sqrt{{tanx}\:+\mathrm{1}}\:{dx} \\ $$$${t}^{\mathrm{2}} =\mathrm{1}+{tanx}\:\:\:\rightarrow\mathrm{2}{tdt}={sec}^{\mathrm{2}} {xdx} \\ $$$$\frac{\mathrm{2}{tdt}}{\mathrm{1}+\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }={dx} \\ $$$$\int\frac{{t}×\mathrm{2}{tdt}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}} \\ $$$$\int\frac{\frac{\mathrm{2}}{{t}^{\mathrm{2}} }}{{t}^{\mathrm{2}} +\frac{\mathrm{2}}{{t}^{\mathrm{2}} }−\mathrm{2}}{dt} \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\int\frac{\left(\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} }\right)−\left(\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} }\right)}{\left({t}^{\mathrm{2}} +\frac{\mathrm{2}}{{t}^{\mathrm{2}} }\right)−\mathrm{2}}{dt} \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left[\int\frac{{d}\left({t}−\frac{\sqrt{\mathrm{2}}}{{t}}\right)}{\left({t}−\frac{\sqrt{\mathrm{2}}}{{t}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{2}}−\int\frac{{d}\left({t}+\frac{\sqrt{\mathrm{2}}}{{t}}\right)}{\left({t}+\frac{\sqrt{\mathrm{2}}}{{t}}\right)^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{2}}\right. \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left[\frac{\mathrm{1}}{\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{2}}}×{tan}^{−\mathrm{1}} \left(\frac{\left.{t}−\frac{\sqrt{\mathrm{2}}}{{t}}\right)}{\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{2}\left(\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2}}\right.}{ln}\left(\frac{\left.{t}+\frac{\sqrt{\mathrm{2}}}{{t}}\right)−\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2}\:}}{\left({t}+\frac{\sqrt{\mathrm{2}}}{{t}}\right)+\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2}}}\right)\right. \\ $$$${put}\:{t}=\sqrt{\mathrm{1}+{tanx}}\: \\ $$
