Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 62983 by hovea cw last updated on 27/Jun/19

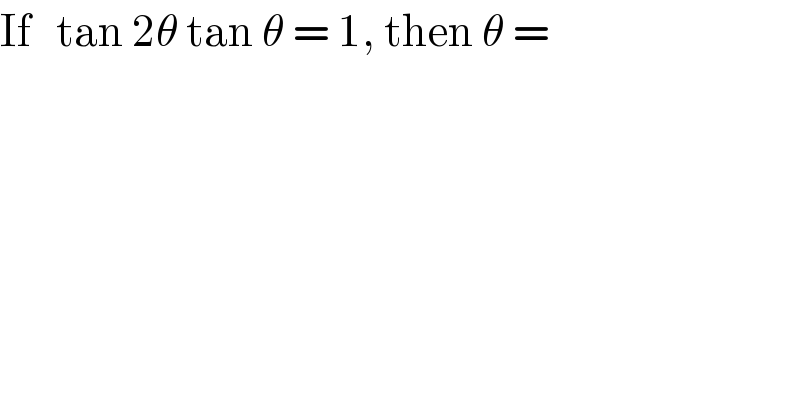
If tan 2θ tan θ = 1, then θ =

$$\mathrm{If}\:\:\:\mathrm{tan}\:\mathrm{2}\theta\:\mathrm{tan}\:\theta\:=\:\mathrm{1},\:\mathrm{then}\:\theta\:= \\ $$

Answered by Hope last updated on 27/Jun/19

tan2θ=cotθ=tan((π/2)−θ) formula [tanα=tanβ α=nπ+β] so 2θ=nπ+((π/2)−θ) 3θ=(((2n+1)π)/2)→ θ=(((2n+1)π)/6)

$${tan}\mathrm{2}\theta={cot}\theta={tan}\left(\frac{\pi}{\mathrm{2}}−\theta\right) \\ $$$${formula} \\ $$$$\left[{tan}\alpha={tan}\beta\:\:\:\alpha={n}\pi+\beta\right] \\ $$$${so}\:\mathrm{2}\theta={n}\pi+\left(\frac{\pi}{\mathrm{2}}−\theta\right) \\ $$$$\mathrm{3}\theta=\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}{\mathrm{2}}\rightarrow\:\theta=\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}{\mathrm{6}} \\ $$

Commented by mr W last updated on 27/Jun/19

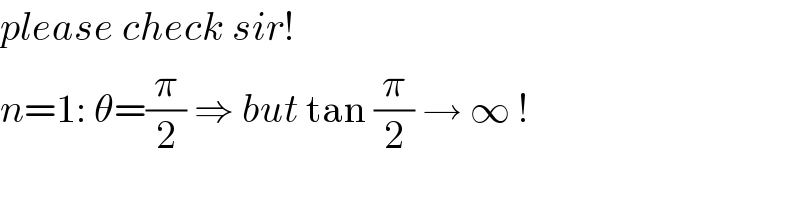
please check sir! n=1: θ=(π/2) ⇒ but tan (π/2) → ∞ !

$${please}\:{check}\:{sir}! \\ $$$${n}=\mathrm{1}:\:\theta=\frac{\pi}{\mathrm{2}}\:\Rightarrow\:{but}\:\mathrm{tan}\:\frac{\pi}{\mathrm{2}}\:\rightarrow\:\infty\:! \\ $$

Commented by Hope last updated on 27/Jun/19

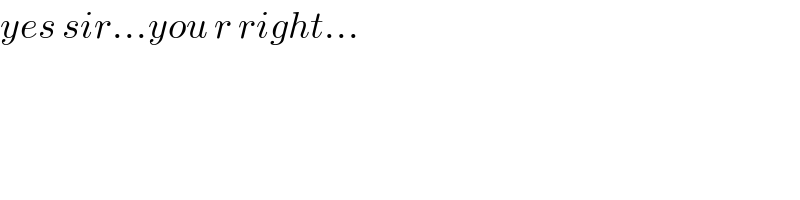
yes sir...you r right...

$${yes}\:{sir}...{you}\:{r}\:{right}... \\ $$

Answered by Hope last updated on 27/Jun/19

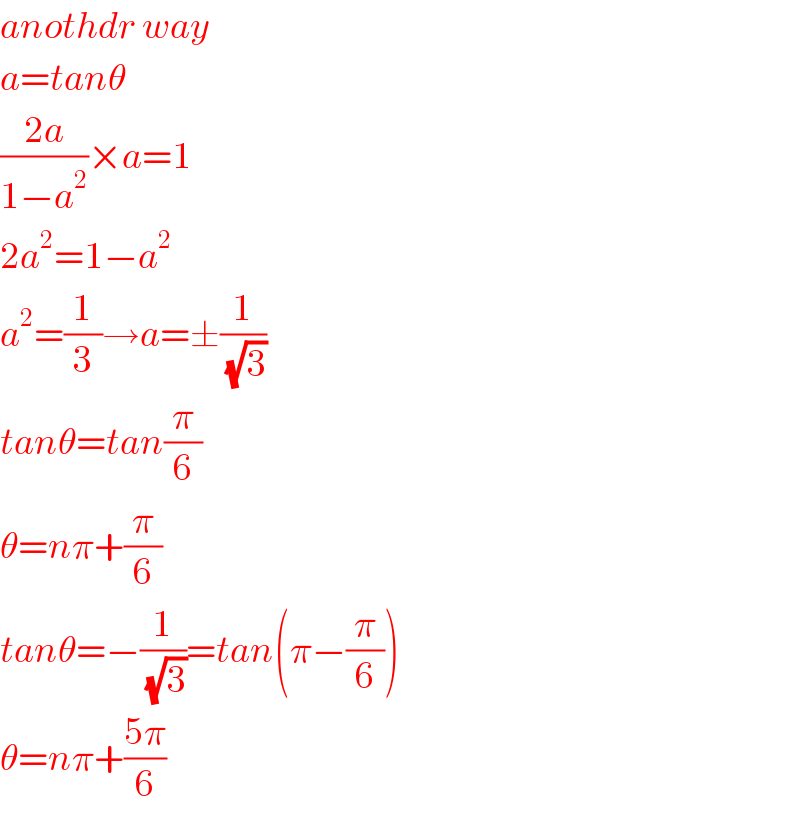
anothdr way a=tanθ ((2a)/(1−a^2 ))×a=1 2a^2 =1−a^2 a^2 =(1/3)→a=±(1/(√3)) tanθ=tan(π/6) θ=nπ+(π/6) tanθ=−(1/(√3))=tan(π−(π/6)) θ=nπ+((5π)/6)

$${anothdr}\:{way} \\ $$$${a}={tan}\theta \\ $$$$\frac{\mathrm{2}{a}}{\mathrm{1}−{a}^{\mathrm{2}} }×{a}=\mathrm{1} \\ $$$$\mathrm{2}{a}^{\mathrm{2}} =\mathrm{1}−{a}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}}\rightarrow{a}=\pm\frac{\mathrm{1}}{\sqrt{\mathrm{3}}} \\ $$$${tan}\theta={tan}\frac{\pi}{\mathrm{6}} \\ $$$$\theta={n}\pi+\frac{\pi}{\mathrm{6}} \\ $$$${tan}\theta=−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}={tan}\left(\pi−\frac{\pi}{\mathrm{6}}\right) \\ $$$$\theta={n}\pi+\frac{\mathrm{5}\pi}{\mathrm{6}} \\ $$

Commented by mr W last updated on 27/Jun/19

good sir! that is θ=nπ±(π/6)

$${good}\:{sir}! \\ $$$${that}\:{is}\:\theta={n}\pi\pm\frac{\pi}{\mathrm{6}} \\ $$

Answered by MJS last updated on 27/Jun/19

tan 2θ =((2sin θ cos θ)/(2cos^2 θ −1)) ((2sin θ cos θ)/(2cos^2 θ −1))×((sin θ)/(cos θ))=1 ((2sin^2 θ)/(2cos^2 θ −1))=1 method 1 2sin^2 θ =2cos^2 θ −1 sin^2 θ −cos^2 θ =−(1/2) 1−2cos^2 θ =−(1/2) cos^2 θ =(3/4) cos θ =±((√3)/2) method 2 ((1−cos 2θ)/(cos 2θ))=1 cos 2θ =(1/2) ...

$$\mathrm{tan}\:\mathrm{2}\theta\:=\frac{\mathrm{2sin}\:\theta\:\mathrm{cos}\:\theta}{\mathrm{2cos}^{\mathrm{2}} \:\theta\:−\mathrm{1}} \\ $$$$\frac{\mathrm{2sin}\:\theta\:\mathrm{cos}\:\theta}{\mathrm{2cos}^{\mathrm{2}} \:\theta\:−\mathrm{1}}×\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}=\mathrm{1} \\ $$$$\frac{\mathrm{2sin}^{\mathrm{2}} \:\theta}{\mathrm{2cos}^{\mathrm{2}} \:\theta\:−\mathrm{1}}=\mathrm{1} \\ $$$$\mathrm{method}\:\mathrm{1} \\ $$$$\mathrm{2sin}^{\mathrm{2}} \:\theta\:=\mathrm{2cos}^{\mathrm{2}} \:\theta\:−\mathrm{1} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\theta\:−\mathrm{cos}^{\mathrm{2}} \:\theta\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{1}−\mathrm{2cos}^{\mathrm{2}} \:\theta\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\theta\:=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{cos}\:\theta\:=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{method}\:\mathrm{2} \\ $$$$\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{cos}\:\mathrm{2}\theta}=\mathrm{1} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com