Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 63021 by kaivan.ahmadi last updated on 27/Jun/19

solve this equation x^y =y^x x,y∈R.

$${solve}\:{this}\:{equation} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{{y}} ={y}^{{x}} \\ $$$$ \\ $$$$ \\ $$$${x},{y}\in\mathbb{R}. \\ $$

Commented by MJS last updated on 28/Jun/19

x=y ∀x, y ∈C\0

$${x}={y}\:\forall{x},\:{y}\:\in\mathbb{C}\backslash\mathrm{0} \\ $$

Commented by kaivan.ahmadi last updated on 28/Jun/19

for x≠y. if x=y there is no thing to solve

$${for}\:{x}\neq{y}. \\ $$$${if}\:{x}={y}\:{there}\:{is}\:{no}\:{thing}\:{to}\:{solve} \\ $$

Commented by malwaan last updated on 28/Jun/19

{2 ; 4} 2^4 = 4^2 =16

$$\left\{\mathrm{2}\:;\:\mathrm{4}\right\} \\ $$$$\mathrm{2}^{\mathrm{4}} \:=\:\mathrm{4}^{\mathrm{2}} \:=\mathrm{16} \\ $$

Answered by MJS last updated on 28/Jun/19

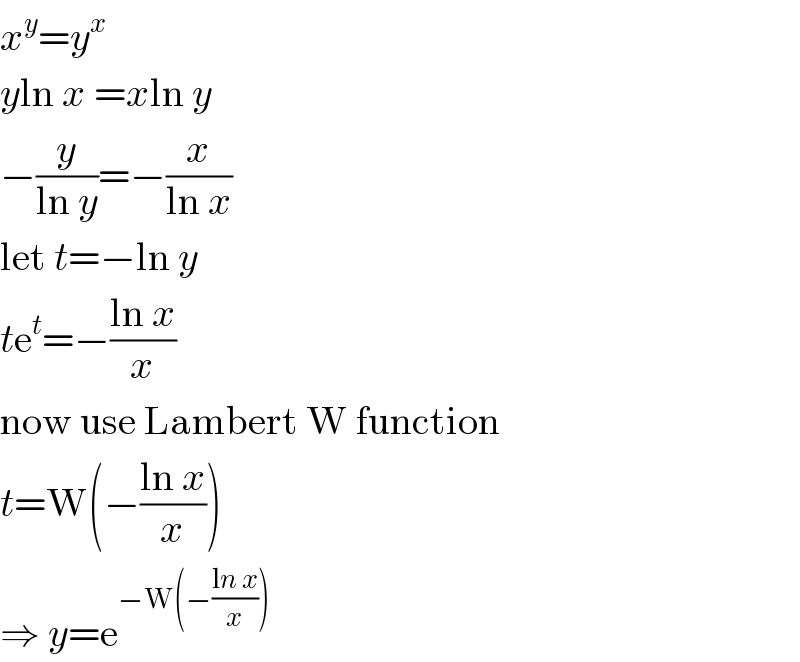
x^y =y^x yln x =xln y −(y/(ln y))=−(x/(ln x)) let t=−ln y te^t =−((ln x)/x) now use Lambert W function t=W(−((ln x)/x)) ⇒ y=e^(−W(−((ln x)/x)))

$${x}^{{y}} ={y}^{{x}} \\ $$$${y}\mathrm{ln}\:{x}\:={x}\mathrm{ln}\:{y} \\ $$$$−\frac{{y}}{\mathrm{ln}\:{y}}=−\frac{{x}}{\mathrm{ln}\:{x}} \\ $$$$\mathrm{let}\:{t}=−\mathrm{ln}\:{y} \\ $$$${t}\mathrm{e}^{{t}} =−\frac{\mathrm{ln}\:{x}}{{x}} \\ $$$$\mathrm{now}\:\mathrm{use}\:\mathrm{Lambert}\:\mathrm{W}\:\mathrm{function} \\ $$$${t}=\mathrm{W}\left(−\frac{\mathrm{ln}\:{x}}{{x}}\right) \\ $$$$\Rightarrow\:{y}=\mathrm{e}^{−\mathrm{W}\left(−\frac{\mathrm{l}{n}\:{x}}{{x}}\right)} \\ $$

Commented by MJS last updated on 28/Jun/19

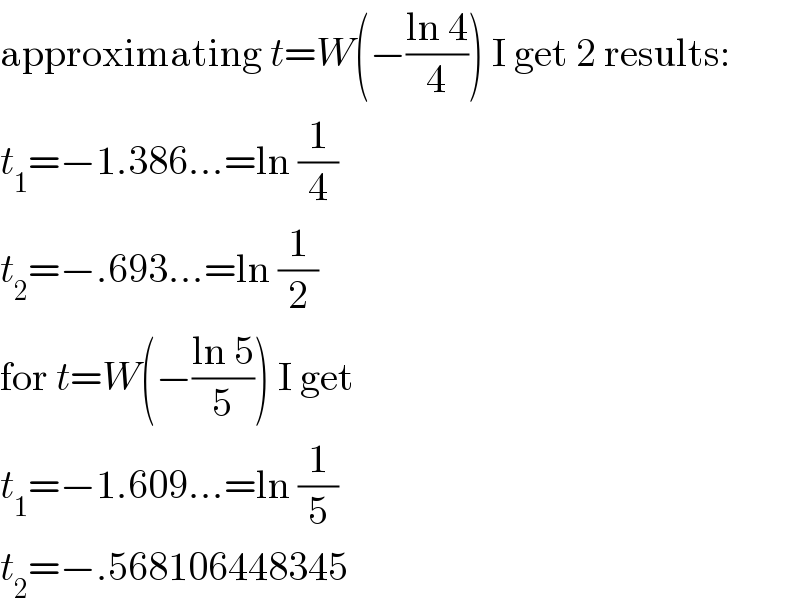
approximating t=W(−((ln 4)/4)) I get 2 results: t_1 =−1.386...=ln (1/4) t_2 =−.693...=ln (1/2) for t=W(−((ln 5)/5)) I get t_1 =−1.609...=ln (1/5) t_2 =−.568106448345

$$\mathrm{approximating}\:{t}={W}\left(−\frac{\mathrm{ln}\:\mathrm{4}}{\mathrm{4}}\right)\:\mathrm{I}\:\mathrm{get}\:\mathrm{2}\:\mathrm{results}: \\ $$$${t}_{\mathrm{1}} =−\mathrm{1}.\mathrm{386}...=\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${t}_{\mathrm{2}} =−.\mathrm{693}...=\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{for}\:{t}={W}\left(−\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{5}}\right)\:\mathrm{I}\:\mathrm{get} \\ $$$${t}_{\mathrm{1}} =−\mathrm{1}.\mathrm{609}...=\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${t}_{\mathrm{2}} =−.\mathrm{568106448345} \\ $$

Commented by mr W last updated on 28/Jun/19

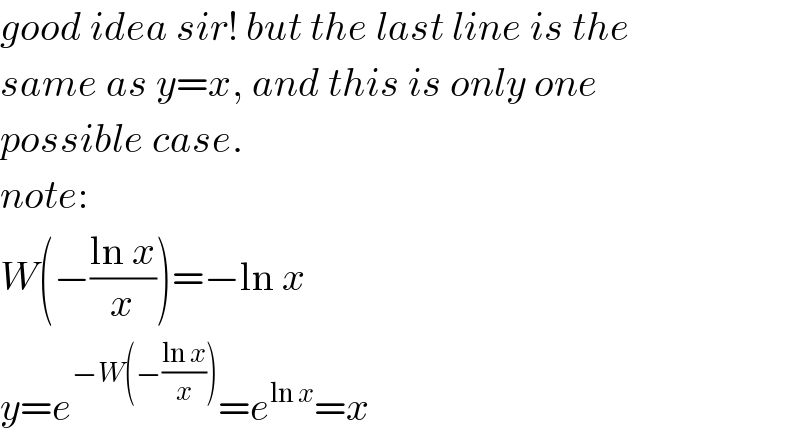
good idea sir! but the last line is the same as y=x, and this is only one possible case. note: W(−((ln x)/x))=−ln x y=e^(−W(−((ln x)/x))) =e^(ln x) =x

$${good}\:{idea}\:{sir}!\:{but}\:{the}\:{last}\:{line}\:{is}\:{the} \\ $$$${same}\:{as}\:{y}={x},\:{and}\:{this}\:{is}\:{only}\:{one} \\ $$$${possible}\:{case}. \\ $$$${note}: \\ $$$${W}\left(−\frac{\mathrm{ln}\:{x}}{{x}}\right)=−\mathrm{ln}\:{x} \\ $$$${y}={e}^{−{W}\left(−\frac{\mathrm{ln}\:{x}}{{x}}\right)} ={e}^{\mathrm{ln}\:{x}} ={x} \\ $$

Commented by mr W last updated on 28/Jun/19

you are right sir! W(−((ln x)/x)) has two values: one is −ln x, the other one differs. so you can generally say y=e^(−W(−((ln x)/x))) .

$${you}\:{are}\:{right}\:{sir}! \\ $$$${W}\left(−\frac{\mathrm{ln}\:{x}}{{x}}\right)\:{has}\:{two}\:{values}:\: \\ $$$${one}\:{is}\:−\mathrm{ln}\:{x},\:{the}\:{other}\:{one}\:{differs}. \\ $$$${so}\:{you}\:{can}\:{generally}\:{say}\:{y}={e}^{−{W}\left(−\frac{\mathrm{ln}\:{x}}{{x}}\right)} . \\ $$

Answered by mr W last updated on 28/Jun/19

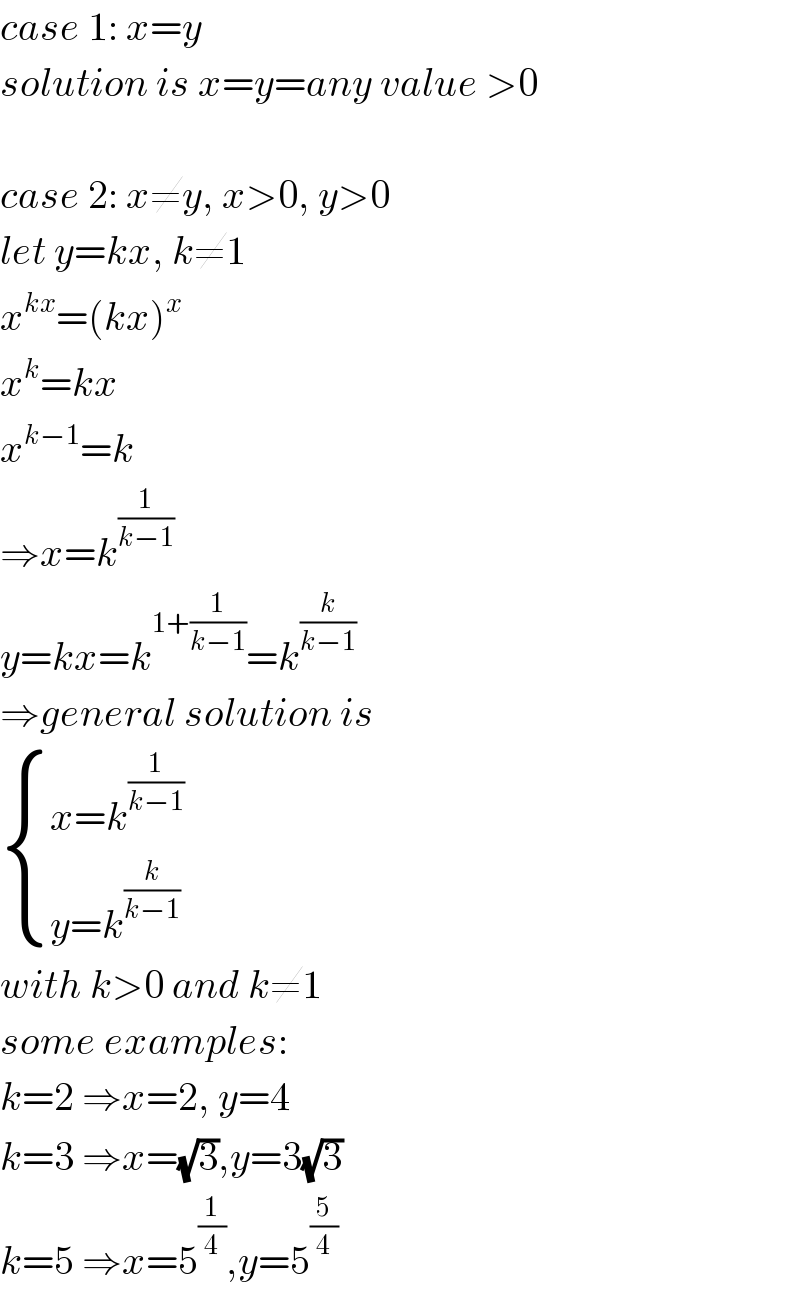
case 1: x=y solution is x=y=any value >0 case 2: x≠y, x>0, y>0 let y=kx, k≠1 x^(kx) =(kx)^x x^k =kx x^(k−1) =k ⇒x=k^(1/(k−1)) y=kx=k^(1+(1/(k−1))) =k^(k/(k−1)) ⇒general solution is { ((x=k^(1/(k−1)) )),((y=k^(k/(k−1)) )) :} with k>0 and k≠1 some examples: k=2 ⇒x=2, y=4 k=3 ⇒x=(√3),y=3(√3) k=5 ⇒x=5^(1/4) ,y=5^(5/4)

$${case}\:\mathrm{1}:\:{x}={y} \\ $$$${solution}\:{is}\:{x}={y}={any}\:{value}\:>\mathrm{0} \\ $$$$ \\ $$$${case}\:\mathrm{2}:\:{x}\neq{y},\:{x}>\mathrm{0},\:{y}>\mathrm{0} \\ $$$${let}\:{y}={kx},\:{k}\neq\mathrm{1} \\ $$$${x}^{{kx}} =\left({kx}\right)^{{x}} \\ $$$${x}^{{k}} ={kx} \\ $$$${x}^{{k}−\mathrm{1}} ={k} \\ $$$$\Rightarrow{x}={k}^{\frac{\mathrm{1}}{{k}−\mathrm{1}}} \\ $$$${y}={kx}={k}^{\mathrm{1}+\frac{\mathrm{1}}{{k}−\mathrm{1}}} ={k}^{\frac{{k}}{{k}−\mathrm{1}}} \\ $$$$\Rightarrow{general}\:{solution}\:{is} \\ $$$$\begin{cases}{{x}={k}^{\frac{\mathrm{1}}{{k}−\mathrm{1}}} }\\{{y}={k}^{\frac{{k}}{{k}−\mathrm{1}}} }\end{cases} \\ $$$${with}\:{k}>\mathrm{0}\:{and}\:{k}\neq\mathrm{1} \\ $$$${some}\:{examples}: \\ $$$${k}=\mathrm{2}\:\Rightarrow{x}=\mathrm{2},\:{y}=\mathrm{4} \\ $$$${k}=\mathrm{3}\:\Rightarrow{x}=\sqrt{\mathrm{3}},{y}=\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${k}=\mathrm{5}\:\Rightarrow{x}=\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}} ,{y}=\mathrm{5}^{\frac{\mathrm{5}}{\mathrm{4}}} \\ $$

Commented by MJS last updated on 28/Jun/19

x^4 =4^x has got 3 solutions x=2∨x=4∨x≈−.766664696 how to get the last one?

$${x}^{\mathrm{4}} =\mathrm{4}^{{x}} \:\mathrm{has}\:\mathrm{got}\:\mathrm{3}\:\mathrm{solutions} \\ $$$${x}=\mathrm{2}\vee{x}=\mathrm{4}\vee{x}\approx−.\mathrm{766664696} \\ $$$$\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{last}\:\mathrm{one}? \\ $$

Commented by kaivan.ahmadi last updated on 28/Jun/19

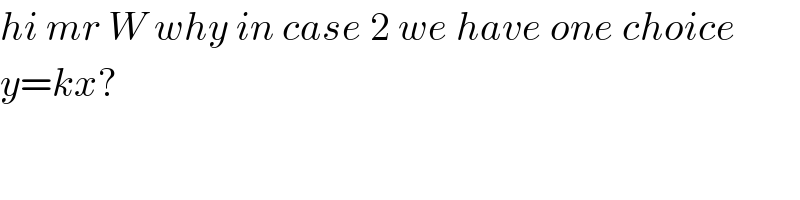
hi mr W why in case 2 we have one choice y=kx?

$${hi}\:{mr}\:{W}\:{why}\:{in}\:{case}\:\mathrm{2}\:{we}\:{have}\:{one}\:{choice} \\ $$$${y}={kx}? \\ $$$$ \\ $$

Commented by kaivan.ahmadi last updated on 28/Jun/19

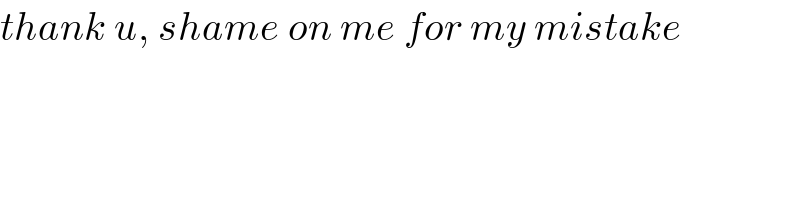
thank u, shame on me for my mistake

$${thank}\:{u},\:{shame}\:{on}\:{me}\:{for}\:{my}\:{mistake} \\ $$

Commented by MJS last updated on 28/Jun/19

x^(kx) =(kx)^x (x^(kx) )^(1/x) =(((kx)^x ))^(1/x) x^k =kx

$${x}^{{kx}} =\left({kx}\right)^{{x}} \\ $$$$\sqrt[{{x}}]{{x}^{{kx}} }=\sqrt[{{x}}]{\left({kx}\right)^{{x}} } \\ $$$${x}^{{k}} ={kx} \\ $$

Commented by MJS last updated on 28/Jun/19

x^(kx) ≠x^k x^x !!! x^(kx) =(x^k )^x =(x^x )^k

$${x}^{{kx}} \neq{x}^{{k}} {x}^{{x}} !!! \\ $$$${x}^{{kx}} =\left({x}^{{k}} \right)^{{x}} =\left({x}^{{x}} \right)^{{k}} \\ $$

Commented by MJS last updated on 28/Jun/19

from mistakes we learn I didn′t immediately see it, so shame on me too

$$\mathrm{from}\:\mathrm{mistakes}\:\mathrm{we}\:\mathrm{learn} \\ $$$$\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{immediately}\:\mathrm{see}\:\mathrm{it},\:\mathrm{so}\:\mathrm{shame}\:\mathrm{on}\:\mathrm{me}\:\mathrm{too} \\ $$

Commented by mr W last updated on 28/Jun/19

MJS sir: when we treat the particular equation x^4 =4^x , it has indeed three roots, one of them is negative. but when we treat generaly x^y =y^x , then the domain of solution is x>0 and y>0. you see this if the particular equation is x^(1.25) =1.25^x which has only two roots, since x>0.

$${MJS}\:{sir}: \\ $$$${when}\:{we}\:{treat}\:{the}\:{particular}\:{equation} \\ $$$${x}^{\mathrm{4}} =\mathrm{4}^{{x}} ,\:{it}\:{has}\:{indeed}\:{three}\:{roots},\:{one} \\ $$$${of}\:{them}\:{is}\:{negative}.\:{but}\:{when}\:{we} \\ $$$${treat}\:{generaly}\:{x}^{{y}} ={y}^{{x}} ,\:{then}\:{the}\:{domain}\:{of} \\ $$$${solution}\:{is}\:{x}>\mathrm{0}\:{and}\:{y}>\mathrm{0}.\:\:{you}\:{see}\:{this} \\ $$$${if}\:{the}\:{particular}\:{equation}\:{is} \\ $$$${x}^{\mathrm{1}.\mathrm{25}} =\mathrm{1}.\mathrm{25}^{{x}} \:{which}\:{has}\:{only}\:{two}\:{roots}, \\ $$$${since}\:{x}>\mathrm{0}. \\ $$

Commented by MJS last updated on 28/Jun/19

you are right x^(2n) =(2n)^x with n∈N∧n>2 has 3 solutions is there a way to get the negative one?

$$\mathrm{you}\:\mathrm{are}\:\mathrm{right} \\ $$$${x}^{\mathrm{2}{n}} =\left(\mathrm{2}{n}\right)^{{x}} \:\mathrm{with}\:{n}\in\mathbb{N}\wedge{n}>\mathrm{2}\:\mathrm{has}\:\mathrm{3}\:\mathrm{solutions} \\ $$$$\mathrm{is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{way}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{negative}\:\mathrm{one}? \\ $$

Commented by mr W last updated on 28/Jun/19

yes! x^(2n) =(2n)^x ⇒x=±(2n)^(x/(2n)) =±e^((x ln (2n))/(2n)) ⇒xe^(−((x ln (2n))/(2n))) =±1 ⇒[−((x ln (2n))/(2n))]e^([−((x ln (2n))/(2n))]) =±((ln (2n))/(2n)) ⇒−((x ln (2n))/(2n))=W[±((ln (2n))/(2n))] ⇒x=−((2n)/(ln (2n)))W[±((ln (2n))/(2n))] this gets three values, one of them is 2n. one of them is negative.

$${yes}! \\ $$$${x}^{\mathrm{2}{n}} =\left(\mathrm{2}{n}\right)^{{x}} \\ $$$$\Rightarrow{x}=\pm\left(\mathrm{2}{n}\right)^{\frac{{x}}{\mathrm{2}{n}}} =\pm{e}^{\frac{{x}\:\mathrm{ln}\:\left(\mathrm{2}{n}\right)}{\mathrm{2}{n}}} \\ $$$$\Rightarrow{xe}^{−\frac{{x}\:\mathrm{ln}\:\left(\mathrm{2}{n}\right)}{\mathrm{2}{n}}} =\pm\mathrm{1} \\ $$$$\Rightarrow\left[−\frac{{x}\:\mathrm{ln}\:\left(\mathrm{2}{n}\right)}{\mathrm{2}{n}}\right]{e}^{\left[−\frac{{x}\:\mathrm{ln}\:\left(\mathrm{2}{n}\right)}{\mathrm{2}{n}}\right]} =\pm\frac{\mathrm{ln}\:\left(\mathrm{2}{n}\right)}{\mathrm{2}{n}} \\ $$$$\Rightarrow−\frac{{x}\:\mathrm{ln}\:\left(\mathrm{2}{n}\right)}{\mathrm{2}{n}}={W}\left[\pm\frac{\mathrm{ln}\:\left(\mathrm{2}{n}\right)}{\mathrm{2}{n}}\right] \\ $$$$\Rightarrow{x}=−\frac{\mathrm{2}{n}}{\mathrm{ln}\:\left(\mathrm{2}{n}\right)}{W}\left[\pm\frac{\mathrm{ln}\:\left(\mathrm{2}{n}\right)}{\mathrm{2}{n}}\right] \\ $$$${this}\:{gets}\:{three}\:{values},\:{one}\:{of}\:{them}\:{is}\:\mathrm{2}{n}. \\ $$$${one}\:{of}\:{them}\:{is}\:{negative}. \\ $$

Commented by MJS last updated on 28/Jun/19

thank you!

$$\mathrm{thank}\:\mathrm{you}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com