∫_0 ^1 ∫_0 ^1 (dy/(1+y(x^2 −x))) dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 63292 by aliesam last updated on 02/Jul/19

$\int_{0}^{1} \int_{0}^{1} \frac{d y}{1 + y (x^{2} - x)} d x$
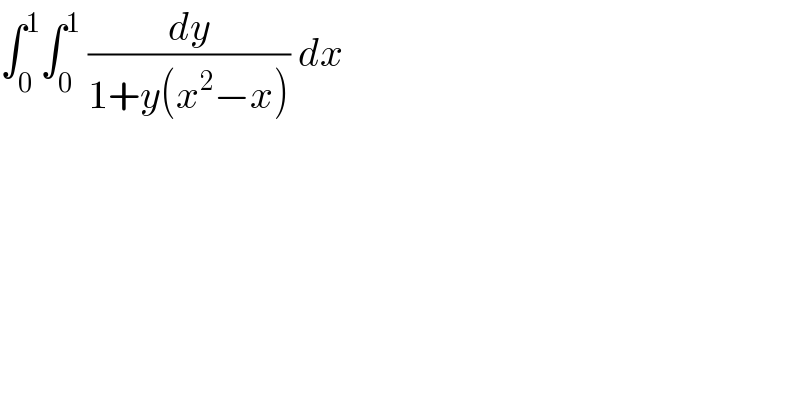
Commented by mathmax by abdo last updated on 02/Jul/19

$l e t I = \int_{0}^{1} \int_{0}^{1} \frac{d y}{1 + (x^{2} - x) y} d x \Rightarrow I = \int_{0}^{1} (\int_{0}^{1} \frac{d y}{1 + (x^{2} - x) y}) d x$ $\int_{0}^{1} \frac{d y}{1 + (x^{2} - x) y} = \frac{1}{x^{2} - x} l n ∣ 1 + (x^{2} - x) y ∣_{y = 0}^{1} = \frac{1}{x^{2} - x} l n ∣ x^{2} - x + 1 ∣$ $= \frac{l n (x^{2} - x + 1)}{x^{2} - x} (b e c a u s e x^{2} - x + 1 > 0) \Rightarrow$ $I = \int_{0}^{1} \frac{l n (x^{2} - x + 1)}{x^{2} - x} d x l e t f (t) = \int_{0}^{1} \frac{l n ({t x}^{2} - x + 1)}{x^{2} - x} d x w i t h t > 0 w e h a v e$ $f^{^{'}} (t) = \int_{0}^{1} \frac{x^{2}}{(x^{2} - x) ({t x}^{2} - x + 1)} d x = \int_{0}^{1} \frac{x}{(x - 1) ({t x}^{2} - x + 1)} d x l e t d e c o m p o s e$
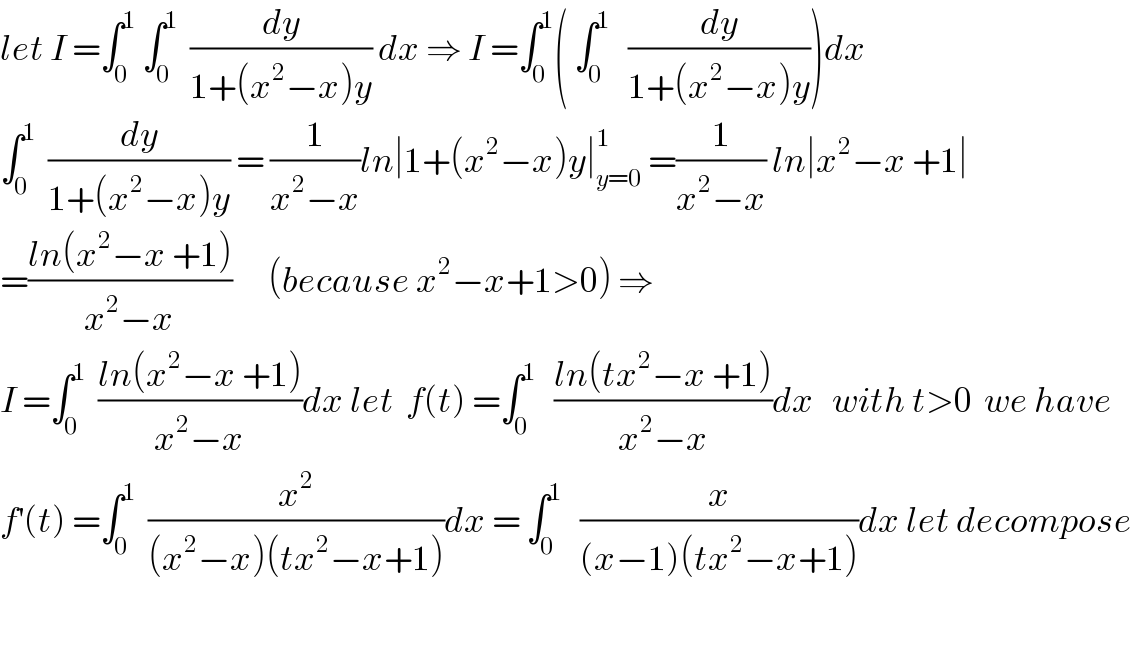
Commented by aliesam last updated on 02/Jul/19

$n i c e s o l u t i o n s i r$
Commented by mathmax by abdo last updated on 02/Jul/19
$let decompose F(x)=(x/((x−1)(tx^2 −x +1))) F(x)=(a/(x−1)) +((bx +c)/(tx^2 −x+1)) a =lim_(x→1) (x−1)F(x) = (1/t) lim_(x→+∞) xF(x) =0 = a+(b/t) ⇒at +b =0 ⇒b =−at =−1 ⇒ F(x) = (1/(t(x−1))) +((−x +c)/(tx^2 −x +1)) F(2) =(2/(4t−1)) =(1/t) +((−2+c)/(4t−1)) ⇒2 =((4t−1)/t) −2 +c ⇒c=4−((4t−1)/t) =(1/t) ⇒ F(t) =(1/(t(x−1))) +((−x+(1/t))/(tx^2 −x+1)) =(1/(t(x−1))) +((−tx +1)/(t(tx^2 −x+1))) ⇒ f^′ (t) =∫_0 ^1 (1/(t(x−1)))dx −(1/t) ∫_0 ^1 ((tx−1)/(tx^2 −x+1))dx =(1/t){∫_0 ^1 (dx/(x−1)) −(1/2)∫_0 ^1 ((2tx−1−1)/(tx^2 −x+1))dx} =(1/t) { [ln∣x−1∣ −(1/2)ln(tx^2 −x+1)]_(x=0) ^1 +(1/2) ∫_0 ^1 (dx/(tx^2 −x+1))} =(1/t){[ ln(((∣x−1∣)/(√(tx^2 −x+1))))]_(x=0) ^1 +(1/2) ∫_0 ^1 (dx/(tx^2 −x+1))}....perhaps the integral diverges... ...be continued....$
$l e t d e c o m p o s e F (x) = \frac{x}{(x - 1) ({t x}^{2} - x + 1)}$ $F (x) = \frac{a}{x - 1} + \frac{b x + c}{{t x}^{2} - x + 1}$ $a = {l i m}_{x \to 1} (x - 1) F (x) = \frac{1}{t}$ ${l i m}_{x \to + \infty} x F (x) = 0 = a + \frac{b}{t} \Rightarrow a t + b = 0 \Rightarrow b = - a t = - 1 \Rightarrow$ $F (x) = \frac{1}{t (x - 1)} + \frac{- x + c}{{t x}^{2} - x + 1}$ $F (2) = \frac{2}{4 t - 1} = \frac{1}{t} + \frac{- 2 + c}{4 t - 1} \Rightarrow 2 = \frac{4 t - 1}{t} - 2 + c \Rightarrow c = 4 - \frac{4 t - 1}{t} = \frac{1}{t} \Rightarrow$ $F (t) = \frac{1}{t (x - 1)} + \frac{- x + \frac{1}{t}}{{t x}^{2} - x + 1} = \frac{1}{t (x - 1)} + \frac{- t x + 1}{t ({t x}^{2} - x + 1)} \Rightarrow$ $f^{^{'}} (t) = \int_{0}^{1} \frac{1}{t (x - 1)} d x - \frac{1}{t} \int_{0}^{1} \frac{t x - 1}{{t x}^{2} - x + 1} d x$ $= \frac{1}{t} {\int_{0}^{1} \frac{d x}{x - 1} - \frac{1}{2} \int_{0}^{1} \frac{2 t x - 1 - 1}{{t x}^{2} - x + 1} d x}$ $= \frac{1}{t} {{[l n ∣ x - 1 ∣ - \frac{1}{2} l n ({t x}^{2} - x + 1)]}_{x = 0}^{1} + \frac{1}{2} \int_{0}^{1} \frac{d x}{{t x}^{2} - x + 1}}$ $= \frac{1}{t} {{[l n (\frac{∣ x - 1 ∣}{\sqrt{{t x}^{2} - x + 1}})]}_{x = 0}^{1} + \frac{1}{2} \int_{0}^{1} \frac{d x}{{t x}^{2} - x + 1}} . . . . p e r h a p s t h e i n t e g r a l d i v e r g e s . . .$ $. . . b e c o n t i n u e d . . . .$
Commented by mathmax by abdo last updated on 02/Jul/19
$let change the ordre of integral I =∫_0 ^1 (∫_0 ^1 (dx/(1+yx^2 −yx)))dy we have A(y)=∫_0 ^1 (dx/(yx^2 −yx +1)) →let solve yx^2 −yx +1 =0 Δ =y^2 −4y <0 due to 0≤y≤1 ⇒yx^2 −yx +1=y(x^2 −x +(1/y)) =y( x^2 −2x(1/2) +(1/4) +(1/y) −(1/4)) =y{ (x−(1/2))^2 +((4−y)/y)} ( y≠0) we use the changement x−(1/2) =(√((4−y)/y))t ⇒t =((2x−1)/2) (√(y/(4−y))) A(y) = ∫_(−(1/2)(√(y/(4−y)))) ^((1/2)(√(y/(4−y)))) (1/(y ((4−y)/y)(1+t^2 ))) (√((4−y)/y))dt =(1/(√(y(4−y)))) [arctan(t)]_(−(1/2)(√(y/(4−y)))) ^((1/2)(√(y/(4−y)))) =((2arctan((1/2)(√(y/(4−y)))))/(√(y(4−y)))) ⇒ I =2 ∫_0 ^1 ((arctan((1/2)(√(y/(4−y)))))/(√(y(4−y)))) dy ....be continued....$
$l e t c h a n g e t h e o r d r e o f i n t e g r a l$ $I = \int_{0}^{1} (\int_{0}^{1} \frac{d x}{1 + {y x}^{2} - y x}) d y w e h a v e$ $A (y) = \int_{0}^{1} \frac{d x}{{y x}^{2} - y x + 1} \to l e t s o l v e {y x}^{2} - y x + 1 = 0$ $Δ = y^{2} - 4 y < 0 d u e t o 0 ⩽ y ⩽ 1 \Rightarrow {y x}^{2} - y x + 1 = y (x^{2} - x + \frac{1}{y})$ $= y (x^{2} - 2 x \frac{1}{2} + \frac{1}{4} + \frac{1}{y} - \frac{1}{4}) = y {{(x - \frac{1}{2})}^{2} + \frac{4 - y}{y}} (y \neq 0)$ $w e u s e t h e c h a n g e m e n t x - \frac{1}{2} = \sqrt{\frac{4 - y}{y}} t \Rightarrow t = \frac{2 x - 1}{2} \sqrt{\frac{y}{4 - y}}$ $A (y) = \int_{- \frac{1}{2} \sqrt{\frac{y}{4 - y}}}^{\frac{1}{2} \sqrt{\frac{y}{4 - y}}} \frac{1}{y \frac{4 - y}{y} (1 + t^{2})} \sqrt{\frac{4 - y}{y}} d t$ $= \frac{1}{\sqrt{y (4 - y)}} {[a r c t a n (t)]}_{- \frac{1}{2} \sqrt{\frac{y}{4 - y}}}^{\frac{1}{2} \sqrt{\frac{y}{4 - y}}} = \frac{2 a r c t a n (\frac{1}{2} \sqrt{\frac{y}{4 - y}})}{\sqrt{y (4 - y)}} \Rightarrow$ $I = 2 \int_{0}^{1} \frac{a r c t a n (\frac{1}{2} \sqrt{\frac{y}{4 - y}})}{\sqrt{y (4 - y)}} d y . . . . b e c o n t i n u e d . . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum