
Question and Answers Forum
Question Number 63372 by necx1 last updated on 03/Jul/19
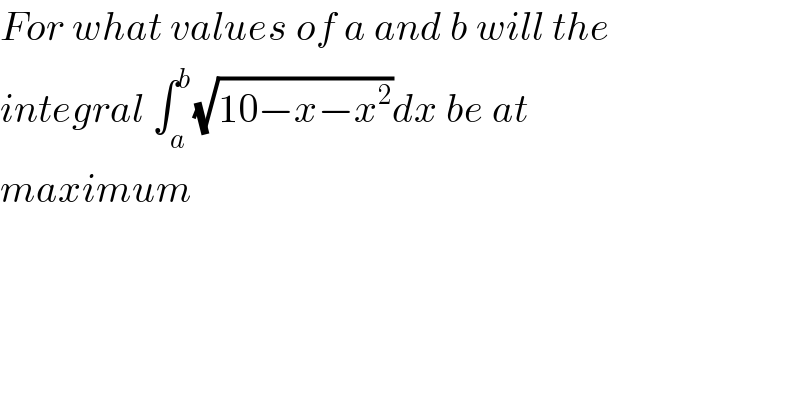
Commented by mr W last updated on 03/Jul/19

Commented by mathmax by abdo last updated on 03/Jul/19
![let f(a,b) =∫_a ^b (√(10−x−x^2 ))dx ⇒f(a,b) =∫_a ^b (√(−(x^2 +x−10)))dx =∫_a ^b (√(−( x^2 +2x(1/2)+(1/4)−(1/4)−10)))dx =∫_a ^b (√(−(x+(1/2))^2 +(1/4)+10))dx =∫_a ^b (√(((41)/4)−(x+(1/2))^2 ))dx changement x+(1/2)=((√(41))/2)sint give f(a,b) =∫_((2a+1)/(√(41))) ^((2b+1)/(√(41))) ((√(41))/2) (√(1−sin^2 t))((√(41))/2)cost dt =((41)/4) ∫_((2a+1)/(√(41))) ^((2b+1)/(√(41))) cos^2 t dt =((41)/8) ∫_((2a+1)/(√(41))) ^((2b+1)/(√(41))) (1+cos(2t))dt =((41)/8){((2b+1)/(√(41))) −((2a+1)/(√(41)))} +((41)/(16)) [sin(2t)]_((2a+1)/(√(41))) ^((2b+1)/(√(41))) =((√(41))/4)(b−a) +((41)/(16)){ sin(((4b+2)/(√(41))))−sin(((4a+2)/(√(41))))} let suppose b≥a (b fixed) (∂f/∂a)(a,b) =−((√(41))/4) −((41)/(16)) (4/(√(41))) cos(((4a+2)/(√(41)))) =−((√(41))/4) −((√(41))/4) cos(((4a+2)/(√(41)))) =−((√(41))/4){ 1+cos(((4a+2)/(√(41))))} =0 ⇒cos(((4a+2)/(√(41))))=cos(π) ⇒ ((4a+2)/(√(41))) =π +2kπ or ((4a+2)/(√(41))) =−π +2kπ ⇒ 4a+2 =(√(41))(2k+1)π or 4a+2 =(√(41))(2k−1)π ⇒ a =(((√(41))(2k+1)π−2)/4) or a =(((√(41))(2k−1)π −2)/4) (k ∈Z) rest to dresz the variation of f(a,b).....be continued...](Q63388.png)
Answered by MJS last updated on 03/Jul/19
![F(x)=∫(√(10−x−x^2 ))dx ∫_a ^b (√(10−x−x^2 ))dx=F(b)−F(a) the maximum for a is at (d/da)[F(b)−F(a)]=(√(10−a−a^2 ))=0 ⇒ a=−(1/2)±((√(41))/2) the maximum for b is similar at b=−(1/2)±((√(41))/2) b>a ⇒ a=−(1/2)−((√(41))/2)∧b=−(1/2)+((√(41))/2)](Q63374.png)
| ||
Question and Answers Forum | ||
Question Number 63372 by necx1 last updated on 03/Jul/19 | ||
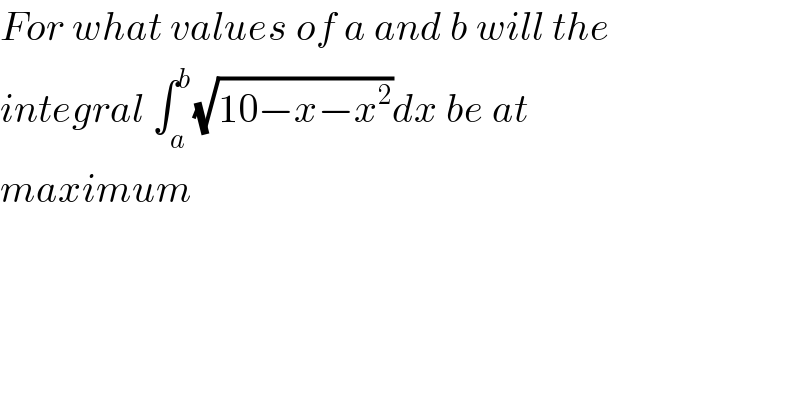 | ||
Commented by mr W last updated on 03/Jul/19 | ||
 | ||
Commented by mathmax by abdo last updated on 03/Jul/19 | ||
![let f(a,b) =∫_a ^b (√(10−x−x^2 ))dx ⇒f(a,b) =∫_a ^b (√(−(x^2 +x−10)))dx =∫_a ^b (√(−( x^2 +2x(1/2)+(1/4)−(1/4)−10)))dx =∫_a ^b (√(−(x+(1/2))^2 +(1/4)+10))dx =∫_a ^b (√(((41)/4)−(x+(1/2))^2 ))dx changement x+(1/2)=((√(41))/2)sint give f(a,b) =∫_((2a+1)/(√(41))) ^((2b+1)/(√(41))) ((√(41))/2) (√(1−sin^2 t))((√(41))/2)cost dt =((41)/4) ∫_((2a+1)/(√(41))) ^((2b+1)/(√(41))) cos^2 t dt =((41)/8) ∫_((2a+1)/(√(41))) ^((2b+1)/(√(41))) (1+cos(2t))dt =((41)/8){((2b+1)/(√(41))) −((2a+1)/(√(41)))} +((41)/(16)) [sin(2t)]_((2a+1)/(√(41))) ^((2b+1)/(√(41))) =((√(41))/4)(b−a) +((41)/(16)){ sin(((4b+2)/(√(41))))−sin(((4a+2)/(√(41))))} let suppose b≥a (b fixed) (∂f/∂a)(a,b) =−((√(41))/4) −((41)/(16)) (4/(√(41))) cos(((4a+2)/(√(41)))) =−((√(41))/4) −((√(41))/4) cos(((4a+2)/(√(41)))) =−((√(41))/4){ 1+cos(((4a+2)/(√(41))))} =0 ⇒cos(((4a+2)/(√(41))))=cos(π) ⇒ ((4a+2)/(√(41))) =π +2kπ or ((4a+2)/(√(41))) =−π +2kπ ⇒ 4a+2 =(√(41))(2k+1)π or 4a+2 =(√(41))(2k−1)π ⇒ a =(((√(41))(2k+1)π−2)/4) or a =(((√(41))(2k−1)π −2)/4) (k ∈Z) rest to dresz the variation of f(a,b).....be continued...](Q63388.png) | ||
Answered by MJS last updated on 03/Jul/19 | ||
![F(x)=∫(√(10−x−x^2 ))dx ∫_a ^b (√(10−x−x^2 ))dx=F(b)−F(a) the maximum for a is at (d/da)[F(b)−F(a)]=(√(10−a−a^2 ))=0 ⇒ a=−(1/2)±((√(41))/2) the maximum for b is similar at b=−(1/2)±((√(41))/2) b>a ⇒ a=−(1/2)−((√(41))/2)∧b=−(1/2)+((√(41))/2)](Q63374.png) | ||
| ||