
Question and Answers Forum
Question Number 63507 by mathmax by abdo last updated on 05/Jul/19
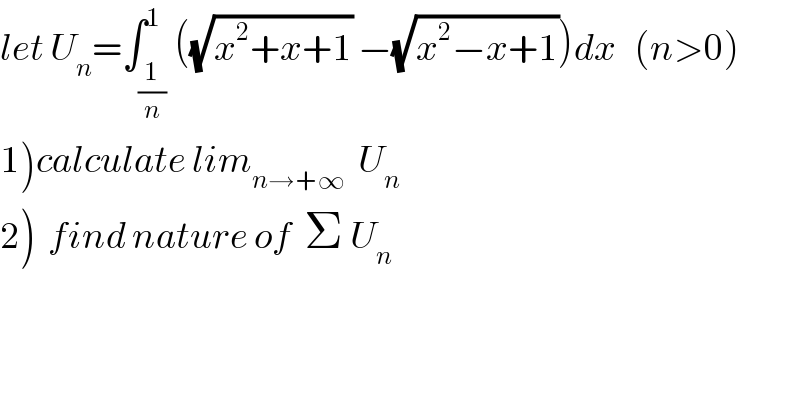
Answered by MJS last updated on 05/Jul/19
![lim_(n→+∞) U_n =∫_0 ^1 ((√(x^2 +x+1))−(√(x^2 −x+1)))dx ∫(√(x^2 ±x+1))dx=(1/2)∫(√((2x±1)^2 +3))dx= [t=sinh^(−1) ((2x±1)/(√3)) → dx=(√(x^2 ±x+1))dt] =(3/4)∫(cosh^2 t)dt=(3/8)∫(1+cosh 2t)dt= =(3/8)t+(3/(16))sinh 2t ∫((√(x^2 +x+1))−(√(x^2 −x+1)))dx= =(3/8)(sinh^(−1) ((2x+1)/(√3)) −sinh^(−1) ((2x−1)/(√3)))+(1/4)((2x+1)(√(x^2 +x+1))−(2x−1)(√(x^2 −x+1)))+C lim_(n→+∞) U_n =∫_0 ^1 ((√(x^2 +x+1))−(√(x^2 −x+1)))dx= =−((3−3(√3))/4)+(3/8)sinh^(−1) (√3) −(9/8)sinh^(−1) ((√3)/3) ≈.424928 [=−((3−3(√3))/4)+(3/8)ln (3+2(√3)) −(3/4)ln 3] ΣU_n =+∞](Q63525.png)
Commented bymathmax by abdo last updated on 05/Jul/19
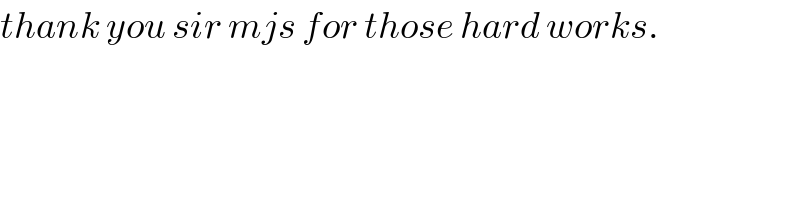
Commented byMJS last updated on 05/Jul/19
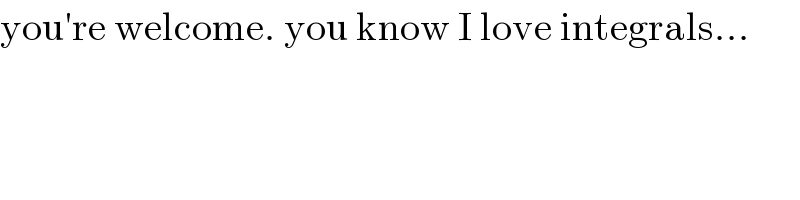
| ||
Question and Answers Forum | ||
Question Number 63507 by mathmax by abdo last updated on 05/Jul/19 | ||
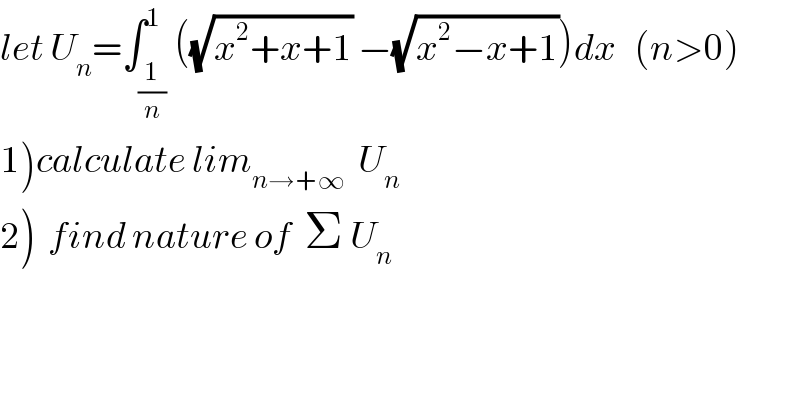 | ||
Answered by MJS last updated on 05/Jul/19 | ||
![lim_(n→+∞) U_n =∫_0 ^1 ((√(x^2 +x+1))−(√(x^2 −x+1)))dx ∫(√(x^2 ±x+1))dx=(1/2)∫(√((2x±1)^2 +3))dx= [t=sinh^(−1) ((2x±1)/(√3)) → dx=(√(x^2 ±x+1))dt] =(3/4)∫(cosh^2 t)dt=(3/8)∫(1+cosh 2t)dt= =(3/8)t+(3/(16))sinh 2t ∫((√(x^2 +x+1))−(√(x^2 −x+1)))dx= =(3/8)(sinh^(−1) ((2x+1)/(√3)) −sinh^(−1) ((2x−1)/(√3)))+(1/4)((2x+1)(√(x^2 +x+1))−(2x−1)(√(x^2 −x+1)))+C lim_(n→+∞) U_n =∫_0 ^1 ((√(x^2 +x+1))−(√(x^2 −x+1)))dx= =−((3−3(√3))/4)+(3/8)sinh^(−1) (√3) −(9/8)sinh^(−1) ((√3)/3) ≈.424928 [=−((3−3(√3))/4)+(3/8)ln (3+2(√3)) −(3/4)ln 3] ΣU_n =+∞](Q63525.png) | ||
| ||
Commented bymathmax by abdo last updated on 05/Jul/19 | ||
 | ||
Commented byMJS last updated on 05/Jul/19 | ||
 | ||