
Question Number 63519 by Rio Michael last updated on 05/Jul/19

$${consider}\:{the}\:{general}\:{definite}\:{intergral}\:\: \\ $$$$\:{I}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{{n}} {xdx} \\ $$$$\left.{a}\right)\:{prove}\:{that}\:{for}\:{n}\geqslant\mathrm{2},\:{nI}_{{n}} =\left({n}−\mathrm{1}\right){I}_{{n}−\mathrm{2}} . \\ $$$$\left.{b}\left.\right)\left.\:{Find}\:{the}\:{values}\:{of}\:\:\boldsymbol{{i}}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{5}} {dx}\:\:\:\boldsymbol{{ii}}\right)\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{6}} {dx} \\ $$
Commented by Prithwish sen last updated on 05/Jul/19
![I_n =∫_0 ^(π/2) sin^(n−1) x sinxdx, using by parts =[−sin^(n−1) xcosx]_0 ^(π/2) + (n−1)∫_0 ^(π/2) sin^(n−2) x(1−sin^2 x)^ dx = (n−1)I_(n−2) −(n−1)I_n nI_n = (n−1)I_(n−2) proved ∫_0 ^(π/2) sin^5 x dx = (((5−1))/5)I_3 = (4/5).(((3−1))/3) I_(3−2) = (4/5).(2/3).I =(8/(15 )) ∫_0 ^(π/2) sinx dx = −(8/(15)) (cosx)_0 ^(π/2) = (8/(15)) similarly you can deduce (ii)](Q63523.png)
$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{n}−\mathrm{1}} \mathrm{x}\:\mathrm{sinxdx},\:\:\mathrm{using}\:\mathrm{by}\:\mathrm{parts} \\ $$$$=\left[−\mathrm{sin}^{\mathrm{n}−\mathrm{1}} \mathrm{xcosx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:+\:\left(\mathrm{n}−\mathrm{1}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{n}−\mathrm{2}} \mathrm{x}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\overset{} {\right)}\mathrm{dx} \\ $$$$=\:\left(\mathrm{n}−\mathrm{1}\right)\mathrm{I}_{\mathrm{n}−\mathrm{2}} −\left(\mathrm{n}−\mathrm{1}\right)\mathrm{I}_{\mathrm{n}} \\ $$$$\mathrm{nI}_{\mathrm{n}} \:=\:\left(\mathrm{n}−\mathrm{1}\right)\mathrm{I}_{\mathrm{n}−\mathrm{2}} \:\:\:\boldsymbol{\mathrm{proved}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{5}} \mathrm{x}\:\mathrm{dx}\:=\:\frac{\left(\mathrm{5}−\mathrm{1}\right)}{\mathrm{5}}\mathrm{I}_{\mathrm{3}} \:=\:\frac{\mathrm{4}}{\mathrm{5}}.\frac{\left(\mathrm{3}−\mathrm{1}\right)}{\mathrm{3}}\:\mathrm{I}_{\mathrm{3}−\mathrm{2}} =\:\frac{\mathrm{4}}{\mathrm{5}}.\frac{\mathrm{2}}{\mathrm{3}}.\mathrm{I} \\ $$$$\:=\frac{\mathrm{8}}{\mathrm{15}\:}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sinx}\:\mathrm{dx}\:=\:−\frac{\mathrm{8}}{\mathrm{15}}\:\left(\mathrm{cosx}\right)_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\:\frac{\mathrm{8}}{\mathrm{15}} \\ $$$$\mathrm{similarly}\:\mathrm{you}\:\mathrm{can}\:\mathrm{deduce}\:\left(\mathrm{ii}\right) \\ $$$$ \\ $$
Commented by Rio Michael last updated on 05/Jul/19
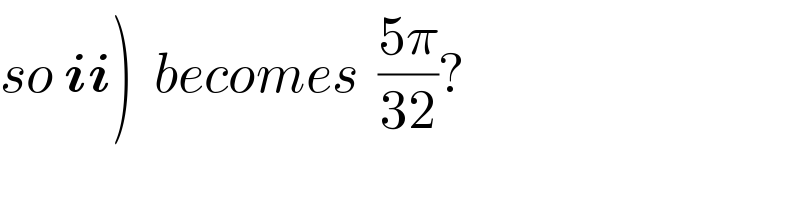
$$\left.{so}\:\boldsymbol{{ii}}\right)\:\:{becomes}\:\:\frac{\mathrm{5}\pi}{\mathrm{32}}? \\ $$
Commented by Prithwish sen last updated on 05/Jul/19

$$\mathrm{yes} \\ $$
Commented by Rio Michael last updated on 05/Jul/19
$${okay}\:{sir}\:{thanks}\: \\ $$
