Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 63552 by minh2001 last updated on 05/Jul/19

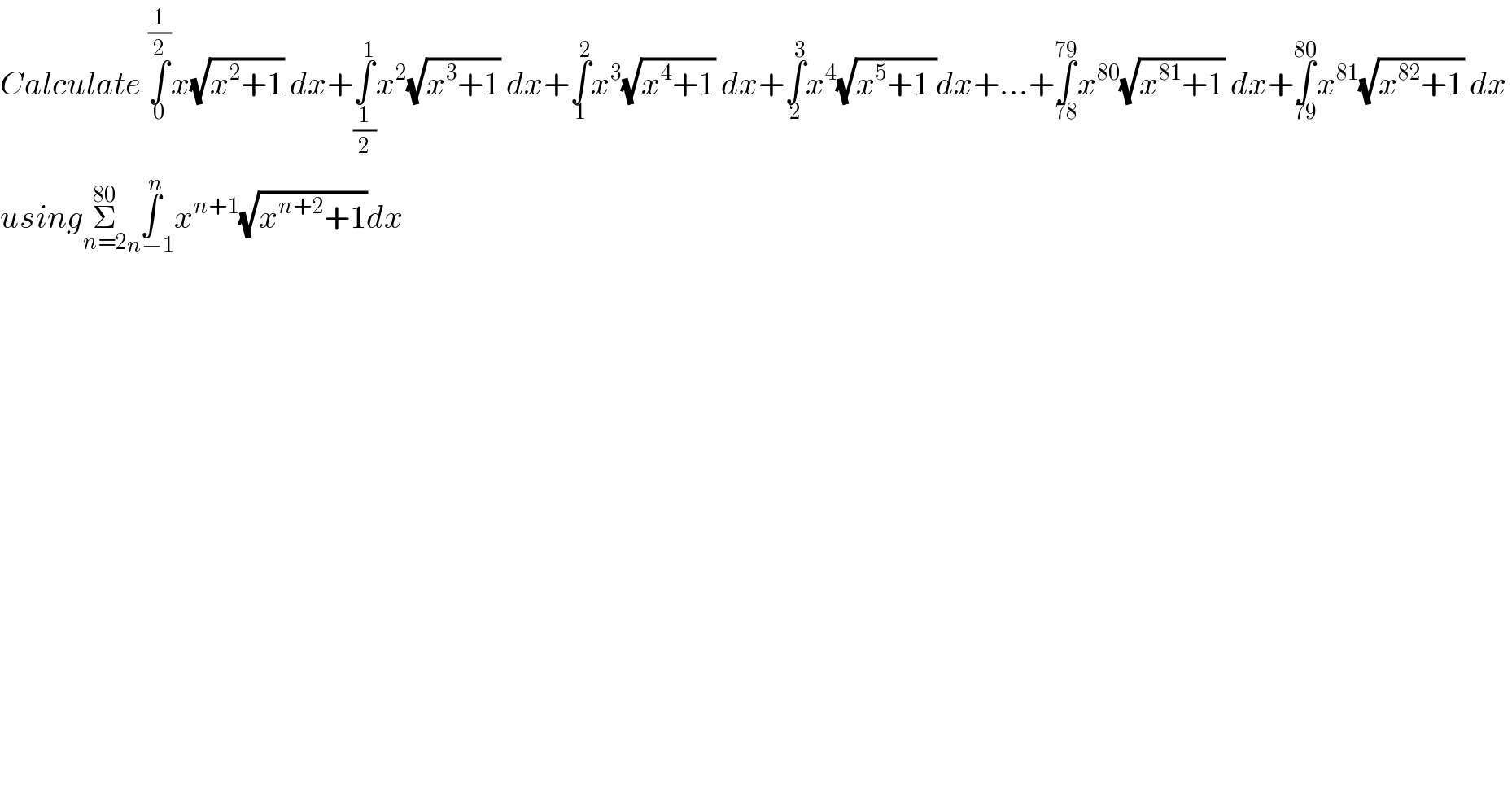
Calculate ∫_0 ^(1/2) x(√(x^2 +1)) dx+∫_(1/2) ^1 x^2 (√(x^3 +1)) dx+∫_1 ^2 x^3 (√(x^4 +1)) dx+∫_2 ^3 x^4 (√(x^5 +1 ))dx+...+∫_(78) ^(79) x^(80) (√(x^(81) +1)) dx+∫_(79) ^(80) x^(81) (√(x^(82) +1)) dx usingΣ_(n=2) ^(80) ∫_(n−1) ^n x^(n+1) (√(x^(n+2) +1))dx

$${Calculate}\:\underset{\mathrm{0}} {\overset{\frac{\mathrm{1}}{\mathrm{2}}} {\int}}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}+\underset{\frac{\mathrm{1}}{\mathrm{2}}} {\overset{\mathrm{1}} {\int}}{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\:{dx}+\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{4}} +\mathrm{1}}\:{dx}+\underset{\mathrm{2}} {\overset{\mathrm{3}} {\int}}{x}^{\mathrm{4}} \sqrt{{x}^{\mathrm{5}} +\mathrm{1}\:}{dx}+...+\underset{\mathrm{78}} {\overset{\mathrm{79}} {\int}}{x}^{\mathrm{80}} \sqrt{{x}^{\mathrm{81}} +\mathrm{1}}\:{dx}+\underset{\mathrm{79}} {\overset{\mathrm{80}} {\int}}{x}^{\mathrm{81}} \sqrt{{x}^{\mathrm{82}} +\mathrm{1}}\:{dx} \\ $$$${using}\underset{{n}=\mathrm{2}} {\overset{\mathrm{80}} {\sum}}\underset{{n}−\mathrm{1}} {\overset{{n}} {\int}}{x}^{{n}+\mathrm{1}} \sqrt{{x}^{{n}+\mathrm{2}} +\mathrm{1}}{dx} \\ $$

Commented by Prithwish sen last updated on 05/Jul/19

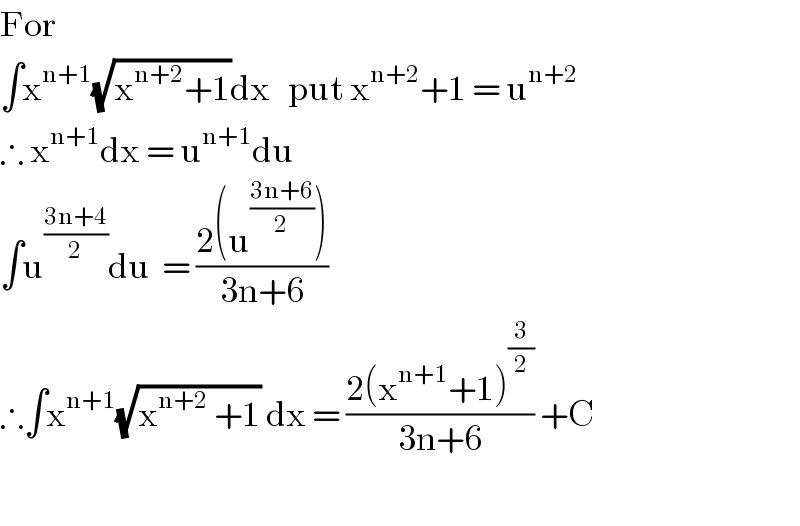
For ∫x^(n+1) (√(x^(n+2) +1))dx put x^(n+2) +1 = u^(n+2) ∴ x^(n+1) dx = u^(n+1) du ∫u^((3n+4)/2) du = ((2(u^((3n+6)/2) ))/(3n+6)) ∴∫x^(n+1) (√(x^(n+2) +1)) dx = ((2(x^(n+1) +1)^(3/2) )/(3n+6)) +C

$$\mathrm{For} \\ $$$$\int\mathrm{x}^{\mathrm{n}+\mathrm{1}} \sqrt{\mathrm{x}^{\mathrm{n}+\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:\:\:\mathrm{put}\:\mathrm{x}^{\mathrm{n}+\mathrm{2}} +\mathrm{1}\:=\:\mathrm{u}^{\mathrm{n}+\mathrm{2}} \\ $$$$\therefore\:\mathrm{x}^{\mathrm{n}+\mathrm{1}} \mathrm{dx}\:=\:\mathrm{u}^{\mathrm{n}+\mathrm{1}} \mathrm{du} \\ $$$$\int\mathrm{u}^{\frac{\mathrm{3n}+\mathrm{4}}{\mathrm{2}}} \mathrm{du}\:\:=\:\frac{\mathrm{2}\left(\mathrm{u}^{\frac{\mathrm{3n}+\mathrm{6}}{\mathrm{2}}} \right)}{\mathrm{3n}+\mathrm{6}} \\ $$$$\therefore\int\mathrm{x}^{\mathrm{n}+\mathrm{1}} \sqrt{\mathrm{x}^{\mathrm{n}+\mathrm{2}} \:+\mathrm{1}}\:\mathrm{dx}\:=\:\frac{\mathrm{2}\left(\mathrm{x}^{\mathrm{n}+\mathrm{1}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3n}+\mathrm{6}}\:+\mathrm{C} \\ $$$$ \\ $$

Answered by MJS last updated on 05/Jul/19

∫x^(n+1) (√(x^(n+2) +1))dx=((2(√((x^(n+2) +1)^3 )))/(3(n+2)))+C ∫_(n−1) ^n x^(n+1) (√(x^(n+2) +1))dx=(2/(3(n+2)))((√((n^(n+2) +1)^3 ))−(√(((n−1)^(n+2) +1)^3 ))) I don′t see how we can sum this up for n=80 this integral is ≈7.69526×10^(231)

$$\int{x}^{{n}+\mathrm{1}} \sqrt{{x}^{{n}+\mathrm{2}} +\mathrm{1}}{dx}=\frac{\mathrm{2}\sqrt{\left({x}^{{n}+\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }}{\mathrm{3}\left({n}+\mathrm{2}\right)}+{C} \\ $$$$\underset{{n}−\mathrm{1}} {\overset{{n}} {\int}}{x}^{{n}+\mathrm{1}} \sqrt{{x}^{{n}+\mathrm{2}} +\mathrm{1}}{dx}=\frac{\mathrm{2}}{\mathrm{3}\left({n}+\mathrm{2}\right)}\left(\sqrt{\left({n}^{{n}+\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }−\sqrt{\left(\left({n}−\mathrm{1}\right)^{{n}+\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\right) \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{see}\:\mathrm{how}\:\mathrm{we}\:\mathrm{can}\:\mathrm{sum}\:\mathrm{this}\:\mathrm{up} \\ $$$${for}\:{n}=\mathrm{80}\:\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\approx\mathrm{7}.\mathrm{69526}×\mathrm{10}^{\mathrm{231}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com