lim_(x→0) ((2^(sec(x)) − 2^(cos(x)) )/x^2 )


Question and Answers Forum

All Questions Topic List
Limits Questions
Previous in All Question Next in All Question
Previous in Limits Next in Limits
Question Number 63579 by Tawa1 last updated on 05/Jul/19

$\lim_{x \to 0} \frac{2^{\sec (x)} - 2^{\cos (x)}}{x^{2}}$
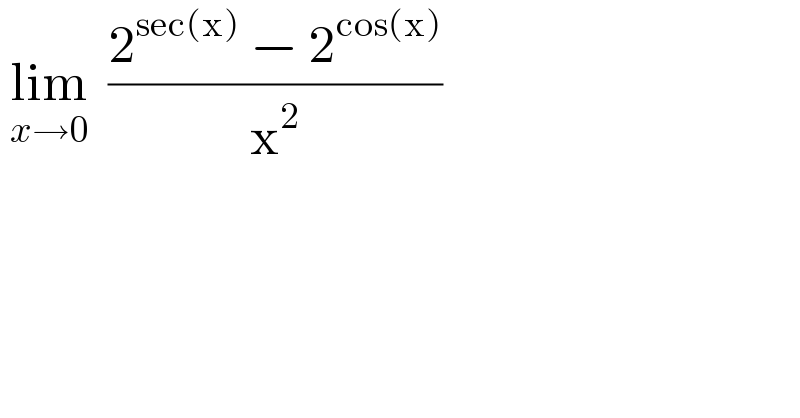
Commented by Prithwish sen last updated on 05/Jul/19

$∵ form \frac{0}{0} applying L^{'} Hopital$ $li \underset{x \to 0}{m} \frac{secx tanx 2^{secx} \ln 2 + sinx 2^{cosx} \ln 2}{2 x}$ $= \frac{1}{2} [li \underset{x \to 0}{m} (\frac{tanx}{x}) . secx 2^{secx} \ln 2 + li \underset{x \to 0}{m} (\frac{sinx}{x}) . 2^{cosx} \ln 2]$ $= 2 \ln 2 please check .$
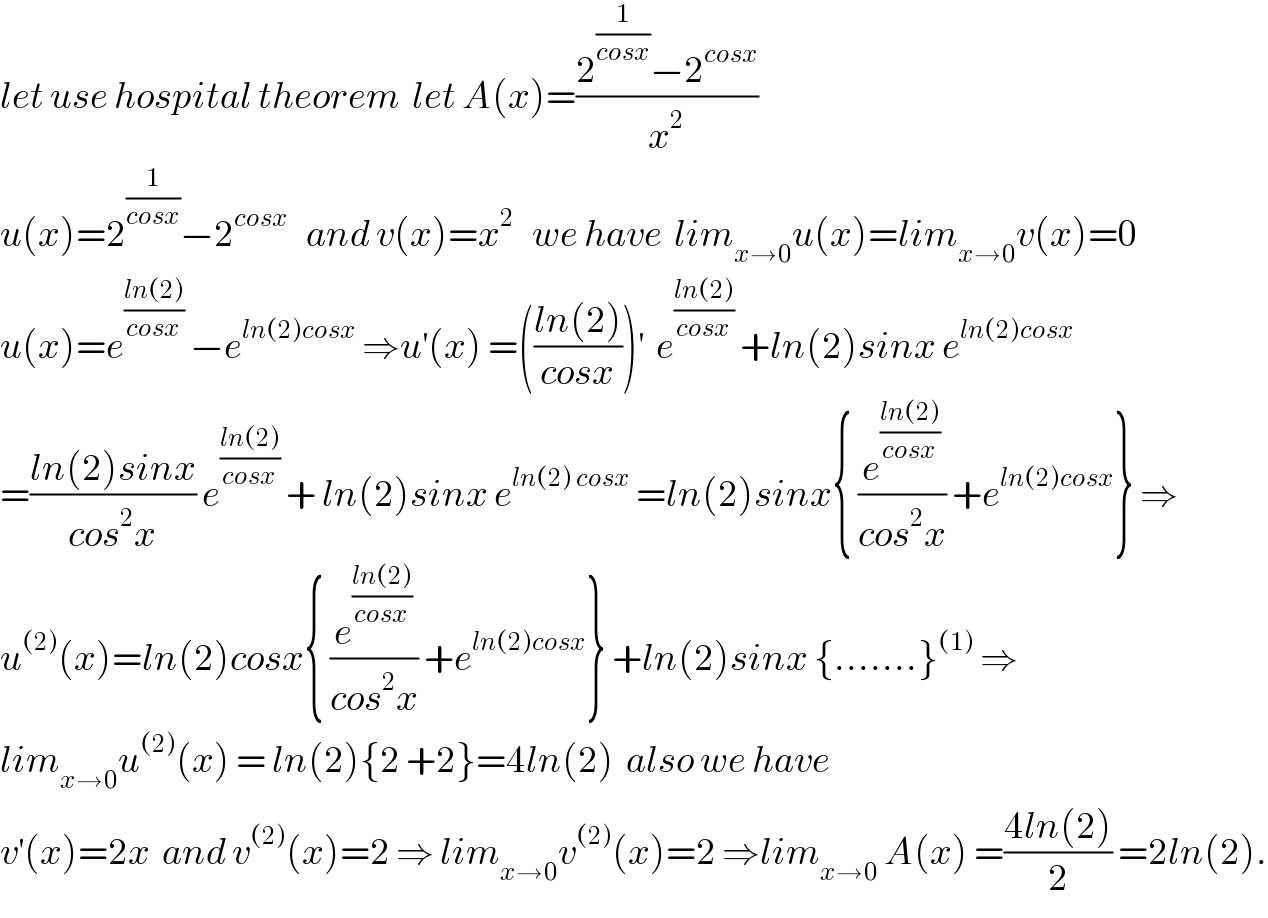
Commented by mathmax by abdo last updated on 05/Jul/19
$let use hospital theorem let A(x)=((2^(1/(cosx)) −2^(cosx) )/x^2 ) u(x)=2^(1/(cosx)) −2^(cosx) and v(x)=x^2 we have lim_(x→0) u(x)=lim_(x→0) v(x)=0 u(x)=e^((ln(2))/(cosx)) −e^(ln(2)cosx) ⇒u^′ (x) =(((ln(2))/(cosx)))^′ e^((ln(2))/(cosx)) +ln(2)sinx e^(ln(2)cosx) =((ln(2)sinx)/(cos^2 x)) e^((ln(2))/(cosx)) + ln(2)sinx e^(ln(2) cosx) =ln(2)sinx{ (e^((ln(2))/(cosx)) /(cos^2 x)) +e^(ln(2)cosx) } ⇒ u^((2)) (x)=ln(2)cosx{ (e^((ln(2))/(cosx)) /(cos^2 x)) +e^(ln(2)cosx) } +ln(2)sinx {.......}^((1)) ⇒ lim_(x→0) u^((2)) (x) = ln(2){2 +2}=4ln(2) also we have v^′ (x)=2x and v^((2)) (x)=2 ⇒ lim_(x→0) v^((2)) (x)=2 ⇒lim_(x→0) A(x) =((4ln(2))/2) =2ln(2).$
$l e t u s e h o s p i t a l t h e o r e m l e t A (x) = \frac{2^{\frac{1}{c o s x}} - 2^{c o s x}}{x^{2}}$ $u (x) = 2^{\frac{1}{c o s x}} - 2^{c o s x} a n d v (x) = x^{2} w e h a v e {l i m}_{x \to 0} u (x) = {l i m}_{x \to 0} v (x) = 0$ $u (x) = e^{\frac{l n (2)}{c o s x}} - e^{l n (2) c o s x} \Rightarrow u^{^{'}} (x) = {(\frac{l n (2)}{c o s x})}^{^{'}} e^{\frac{l n (2)}{c o s x}} + l n (2) s i n x e^{l n (2) c o s x}$ $= \frac{l n (2) s i n x}{{c o s}^{2} x} e^{\frac{l n (2)}{c o s x}} + l n (2) s i n x e^{l n (2) c o s x} = l n (2) s i n x {\frac{e^{\frac{l n (2)}{c o s x}}}{{c o s}^{2} x} + e^{l n (2) c o s x}} \Rightarrow$ $u^{(2)} (x) = l n (2) c o s x {\frac{e^{\frac{l n (2)}{c o s x}}}{{c o s}^{2} x} + e^{l n (2) c o s x}} + l n (2) s i n x {. . . . . . .}^{(1)} \Rightarrow$ ${l i m}_{x \to 0} u^{(2)} (x) = l n (2) {2 + 2} = 4 l n (2) a l s o w e h a v e$ $v^{^{'}} (x) = 2 x a n d v^{(2)} (x) = 2 \Rightarrow {l i m}_{x \to 0} v^{(2)} (x) = 2 \Rightarrow {l i m}_{x \to 0} A (x) = \frac{4 l n (2)}{2} = 2 l n (2) .$
Commented by Tawa1 last updated on 05/Jul/19

$God bless you sir$
Commented by mathmax by abdo last updated on 05/Jul/19

$y o u a r e w e l c o m e .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum